Hash-Based Signatures Part III: Many-times Signatures posted December 2015

We saw previously what were one-time signatures (OTS), then what were few-time signatures (FTS). But now is time to see how to have practical signature schemes based on hash functions. Signature schemes that you can use many times, and ideally as many times as you'd want.

If you haven't read Part I and Part II it's not necessarily a bad thing since we will make abstraction of those. Just think about OTS as a public key/private key pair that you can only use once to sign a message.

Dumb trees

The first idea that comes to mind could be to use a bunch of one-time signatures (use your OTS scheme of preference). The first time you would want to sign something you would use the first OTS keypair, and then never use it again. The second time you would want to sign something, you would use the second OTS keypair, and then never use it again. This can get repetitive and I'm sure you know where I'm going with this. This would also be pretty bad because your public key would consist of all the OTS public keys (and if you want to be able to use your signature scheme a lot, you will have a lot of OTS public keys).

One way of reducing the storage amount, secret-key wise, is to use a seed in a pseudo-random number generator to generate all the secret keys. This way you don't need to store any secret-key, only the seed.

But still, the public key is way too large to be practical.

Merkle trees

To link all of these OTS public keys to one main public keys, there is one very easy way, it's to use a Merkle tree. A solution invented by Merkle in 1979 but published a decade later because of some uninteresting editorial problems.

Here's a very simple definition: a Merkle tree is a basic binary tree where every node is a hash of its childs, the root is our public key and the leaves are the hashes of our OTS public keys. Here's a drawing because one picture is clearer than a thousand words:

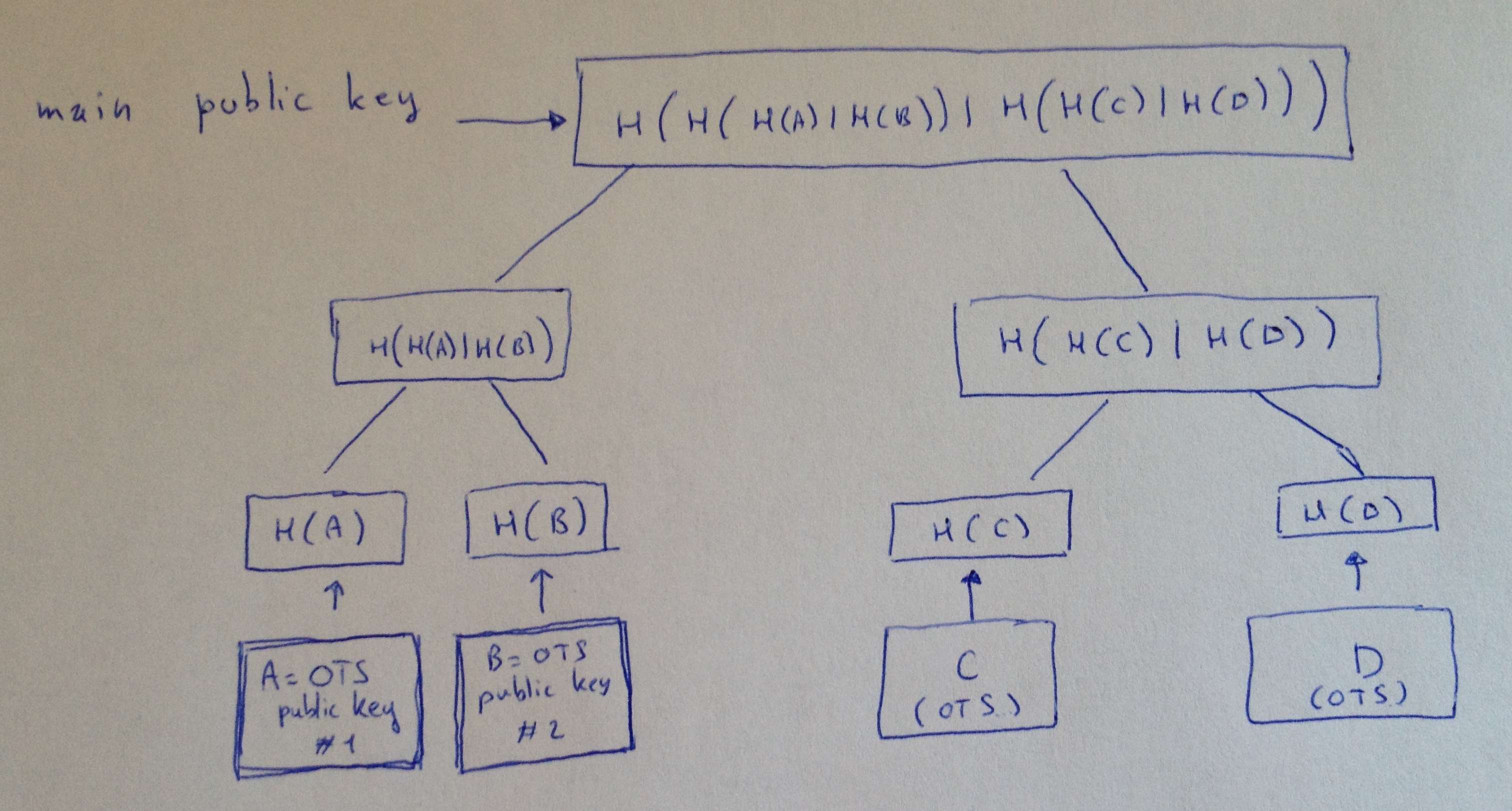
So the first time you would use this tree to sign something: you would use the first OTS public key (A), and then never use it again. Then you would use the B OTS public key, then the C one, and finally the D one. So you can sign 4 messages in total with our example tree. A bigger tree would allow you to sign more messages.

The attractive idea here is that your public key only consist of the root of the tree, and every time you sign something your signature consists of only a few hashes: the authentication path.

In our example, a signature with the first OTS key (A) would be: (1, signature, public key A, authentication path)

• 1 is the index of the signing leaf. You have to keep that in mind: you can't re-use that leaf's OTS. This makes our scheme a stateful scheme.

• The signature is our OTS published secret keys (see the previous parts of this series of articles).

• The public key is our OTS public key, to verify the signature.

• The authentication path is a list of nodes (so a list of hashes) that allows us to recompute the root (our main public key).

Let's understand the authentication path. Here's the previous example with the authentication path highlighted after signing something with the first OTS (A).

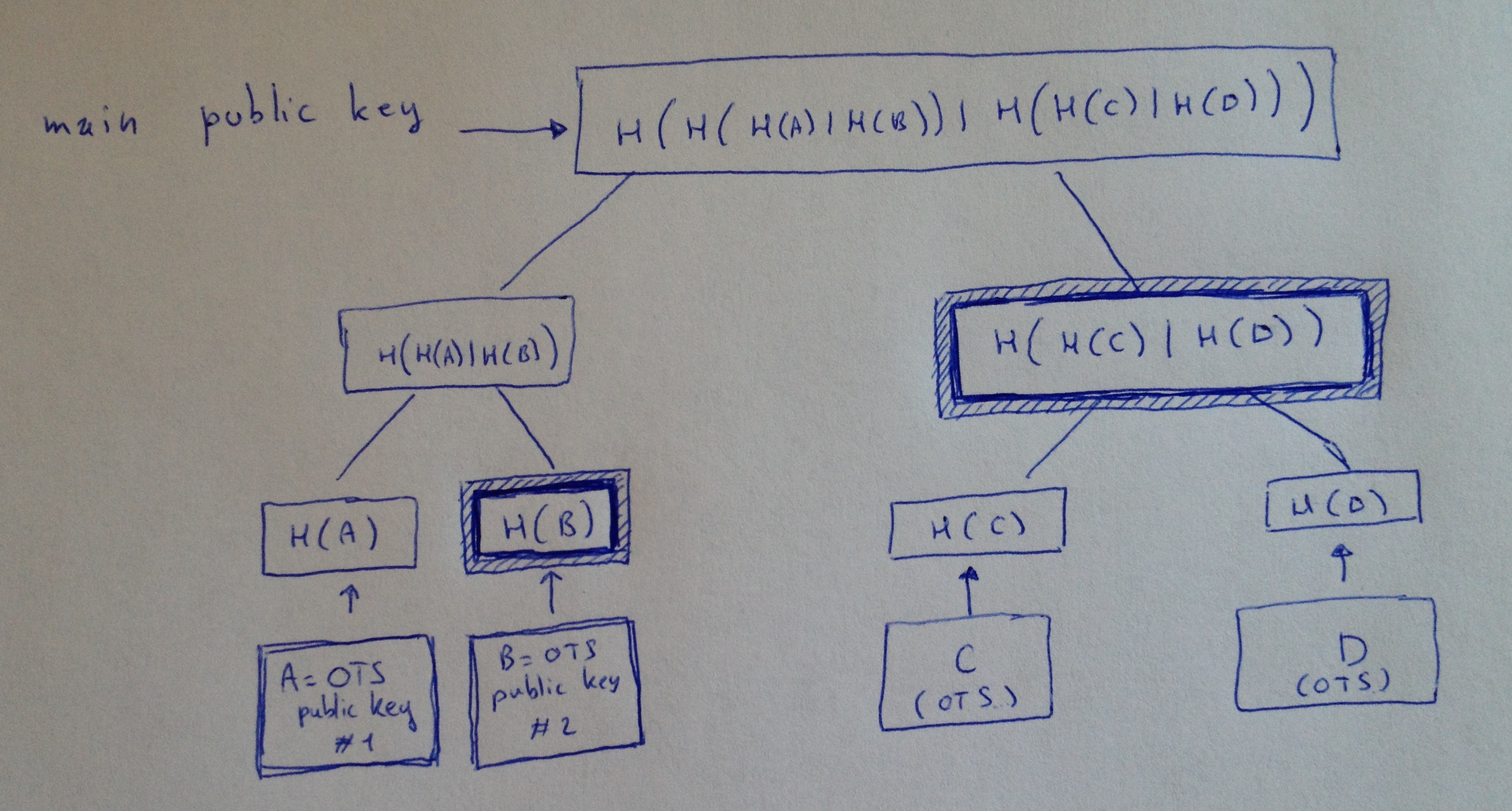
We can see that with our OTS public key, and our two hashes (the neighbor nodes of all the nodes in the path from our signing leaf to the root) we can compute the main public key. And thus we can verify that this was indeed a signature that originated from that main public key.

Thanks to this technique we don't to know all of the OTS public keys to verify that main public key. This saves space and computation.

And that's it, that's the simple concept of the Merkle's signature scheme. A many-times signature scheme based on hashes.

...part IV is here