Hash-Based Signatures Part IV: XMSS and SPHINCS posted December 2015

This post is the ending of a series of blogposts on hash-based signatures. You can find part I here

So now we're getting into the interesting part, the real signatures schemes.

PQCrypto has released an initial recommendations document a few months ago. The two post-quantum algorithms advised there were XMSS and SPHINCS:

This blogpost will be presenting XMSS, a stateful signature scheme, while the next will focus on SPHINCS, the first stateless signature scheme!

XMSS

The eXtended Merkle Signature Scheme (XMSS) was introduced in 2011 and became an internet-draft in 2015.

The main construction looks like a Merkle tree, excepts a few things. The XMSS tree has a mask XORed to the child nodes before getting hashed in their parents node. It's a different mask for every node:

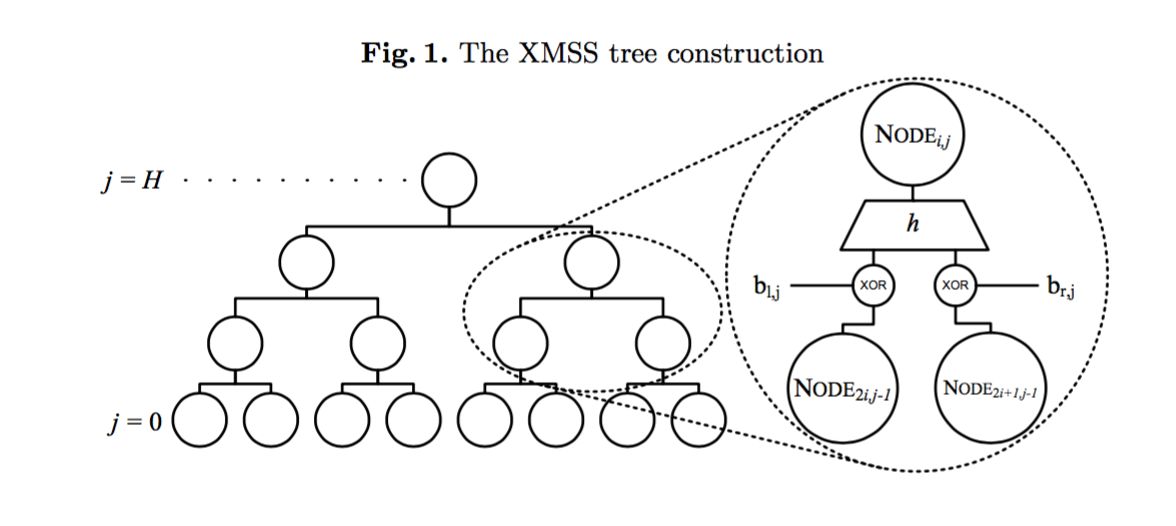
The second particularity is that a leaf of the XMSS tree is not a hash of a one-time signature public key, but the root of another tree called a L-tree.

A L-tree has the same idea of masks applied to its nodes hashes, different from the main XMSS Trees, but common to all the L-trees.

Inside the leaves of any L-tree are stored the elements of a WOTS+ public key. This scheme is explained at the end of the first article of this series.

If like me you're wondering why they store a WOTS+ public key in a tree, here's what Huelsing has to say about it:

The tree is not used to store a WOTS public key but to hash it in a way that we can prove that a second-preimage resistant hash function suffices (instead of a collision resistant one).

Also, the main public key is composed of the root node of the XMSS tree as well as the bit masks used in the XMSS tree and a L-tree.

SPHINCS

SPHINCS is the more recent one, combining a good numbers of advances in the field and even more! Bringing the statelessness we were all waiting for.

Yup, this means that you don't have to keep the state anymore. But before explaining how they did that, let's see how SPHINCS works.

First, SPHINCS is made out of many trees.

Let's look at the first tree:

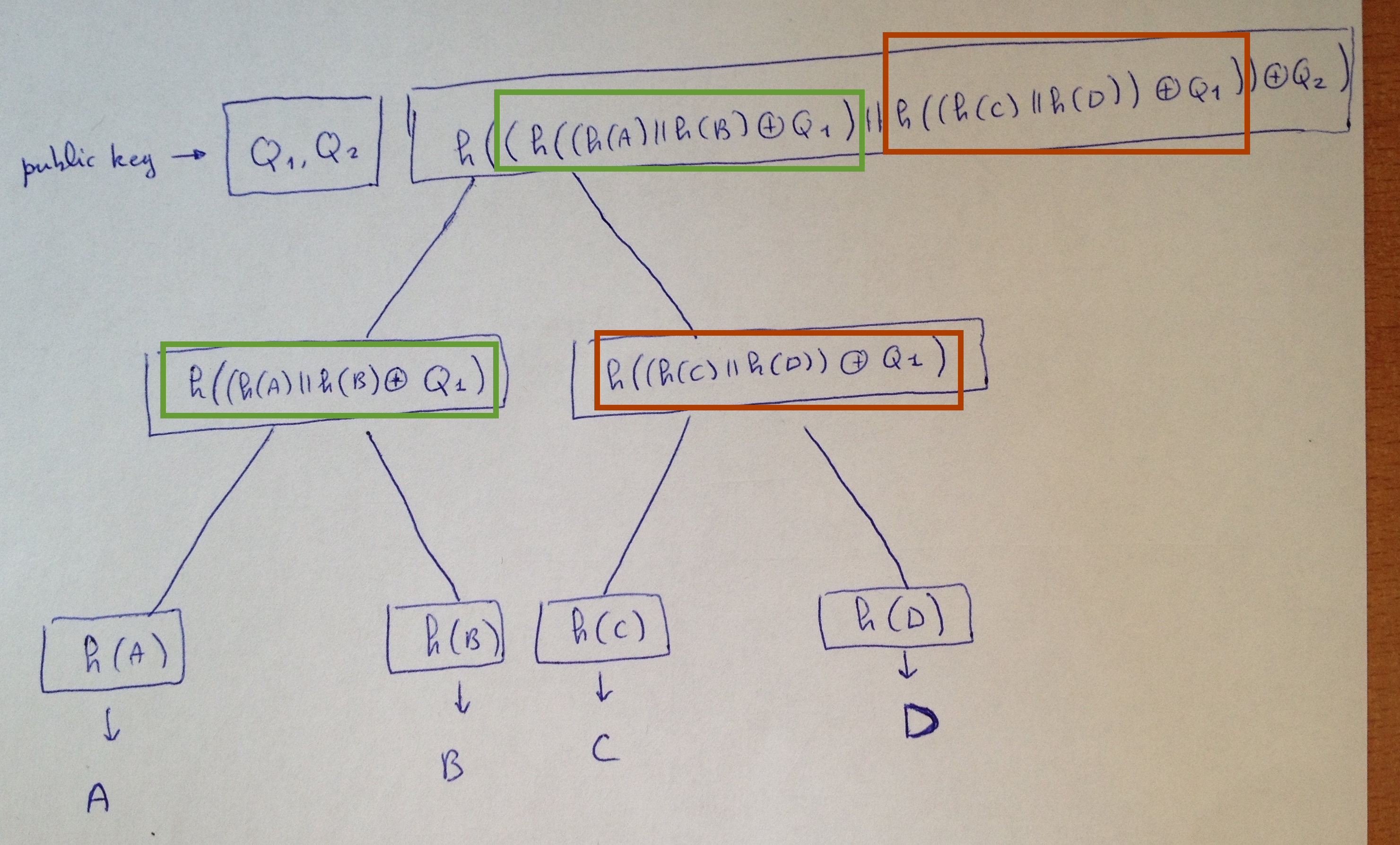
• Each node is the hash of the XOR of the concatenation of the previous nodes with a level bitmask.
• The public key is the root hash along with the bitmasks.
• The leaves of the tree are the compressed public keys of WOTS+ L-trees.

See the WOTS+ L-trees as the same XMSS L-tree we previously explained, except that the bitmask part looks more like a SPHINCS hash tree (a unique mask per level).

Each leaves, containing one Winternitz one-time signature, allow us to sign another tree. So that we know have a second layer of 4 SPHINCS trees, containing themselves WOTS+ public keys at their leaves.

This go on and on... according to your initial parameter. Finally when you reach the layer 0, the WOTS+ signatures won't sign other SPHINCS trees but HORS trees.

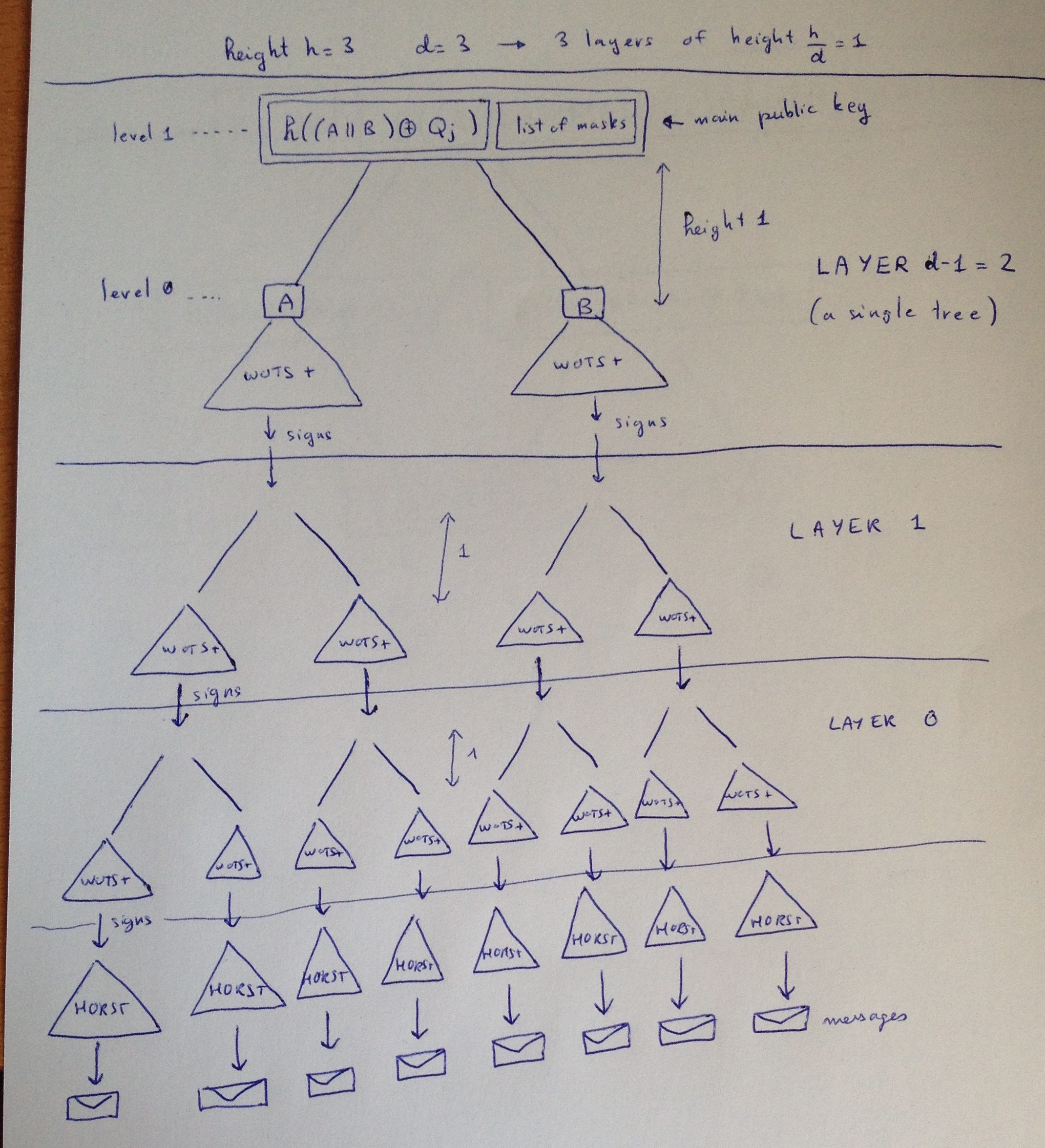
A HORST or HORS tree is the same as a L-tree but this time containing a HORS few-time signature instead of a Winternitz one-time signature. We will use them to sign our messages, and this will increase the security of the scheme since if we do sign a message with the same HORS key it won't be a disaster.

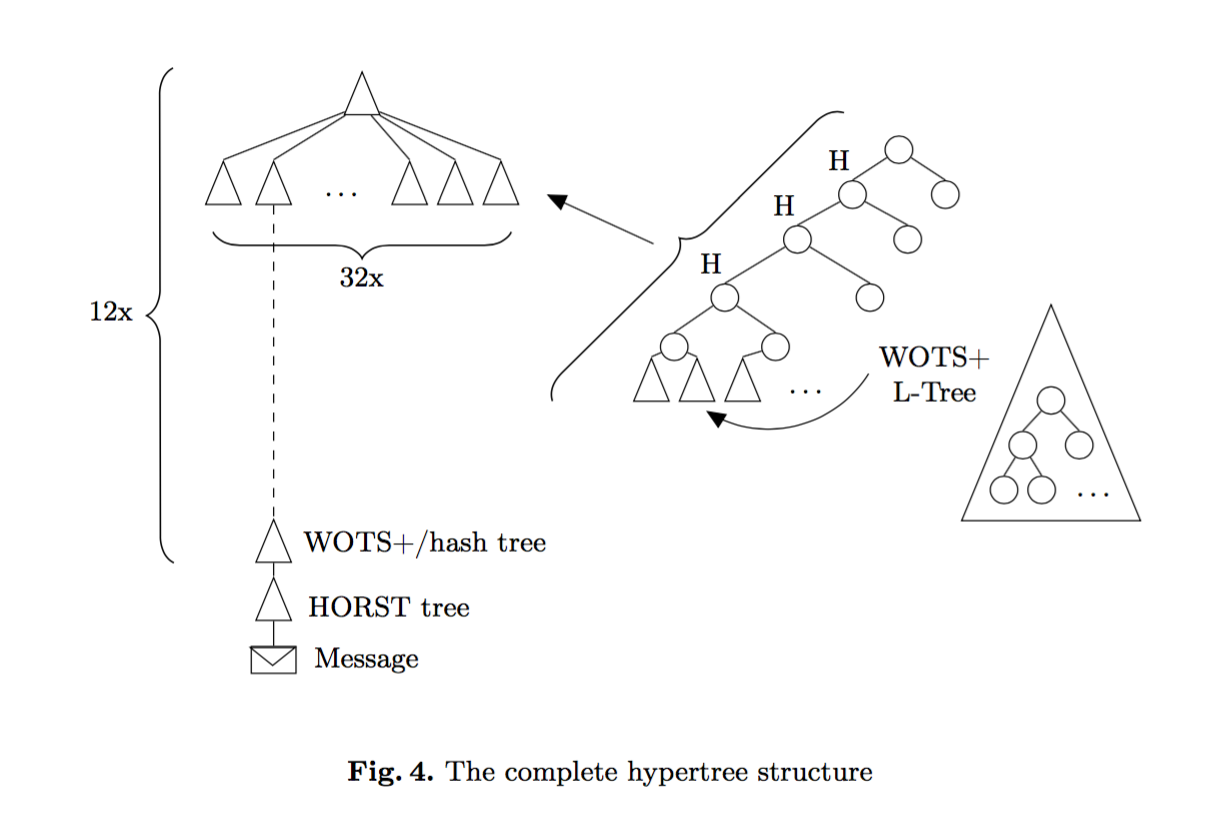
Here's a diagram taken out of the SPHINCS paper making abstraction of WOTS+ L-trees (displaying them as signature of the next SPHINCS tree) and showing only one path to a message.

When signing a message M you first create a "randomized" hash of M and a "random" index. I put random in quotes because everything in SPHINCS is deterministically computed with a PRF. The index now tells you what HORST to pick to sign the randomized hash of M. This is how you get rid of the state: by picking an index deterministically according to the message. Signing the same message again should use the same HORST, signing two different messages should make use of two different HORST with good probabilities.

And this is how this series end!

EDIT: here's another diagram from Armed SPHINCS, I find it pretty nice!