How to check if a binary contains the Dual EC backdoor for the NSA posted December 2015

tl;dr:

this is what you should type:

strings your_binary | grep -C5 -i "c97445f45cdef9f0d3e05e1e585fc297235b82b5be8ff3efca67c59852018192\|8e722de3125bddb05580164bfe20b8b432216a62926c57502ceede31c47816edd1e89769124179d0b695106428815065\|1b9fa3e518d683c6b65763694ac8efbaec6fab44f2276171a42726507dd08add4c3b3f4c1ebc5b1222ddba077f72943b24c3edfa0f85fe24d0c8c01591f0be6f63"

After all the Jupiner fiasco, I wondered how people could look if a binary contained an implementation of Dual EC, and worse, if it contained Dual EC with the NSA's values for P and Q.

The easier thing I could think of is the use of strings to check if the binary contains the hex values of some Dual EC parameters:

strings your_binary | grep -C5 -i `python -c "print '%x' % 115792089210356248762697446949407573530086143415290314195533631308867097853951"`

This is the value of the prime p of the curve P-256. Other curves can be used for Dual EC though, so you should also check for the curve P-384:

strings your_binary | grep -C5 -i `python -c "print '%x' % 39402006196394479212279040100143613805079739270465446667948293404245721771496870329047266088258938001861606973112319"`

and the curve P-521:

strings your_binary | grep -C5 -i `python -c "print '%x' % 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151 "`

I checked the binaries of ScreenOS (taken from here) and they contained these three curves parameters. But this doesn't mean anything, just that these curves are stored, maybe used, maybe used for Dual EC...

To check if it uses the NSA's P and Q, you should grep for P and Q x coordinates from the same NIST paper.

This looks for all the x coordinates of the different P for each curves. This is not that informative since it is the standard point P as a generator of P-256

strings your_binary | grep -C5 -i "6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296\|aa87ca22be8b05378eb1c71ef320ad746e1d3b628ba79b9859f741e082542a385502f25dbf55296c3a545e3872760ab7\|c6858e06b70404e9cd9e3ecb662395b4429c648139053fb521f828af606b4d3dbaa14b5e77efe75928fe1dc127a2ffa8de3348b3c1856a429bf97e7e31c2e5bd66"

Testing the ScreenOS binaries, I get all the matches. This means that the parameters for P-256 and maybe Dual EC are indeed stored in the binaries.

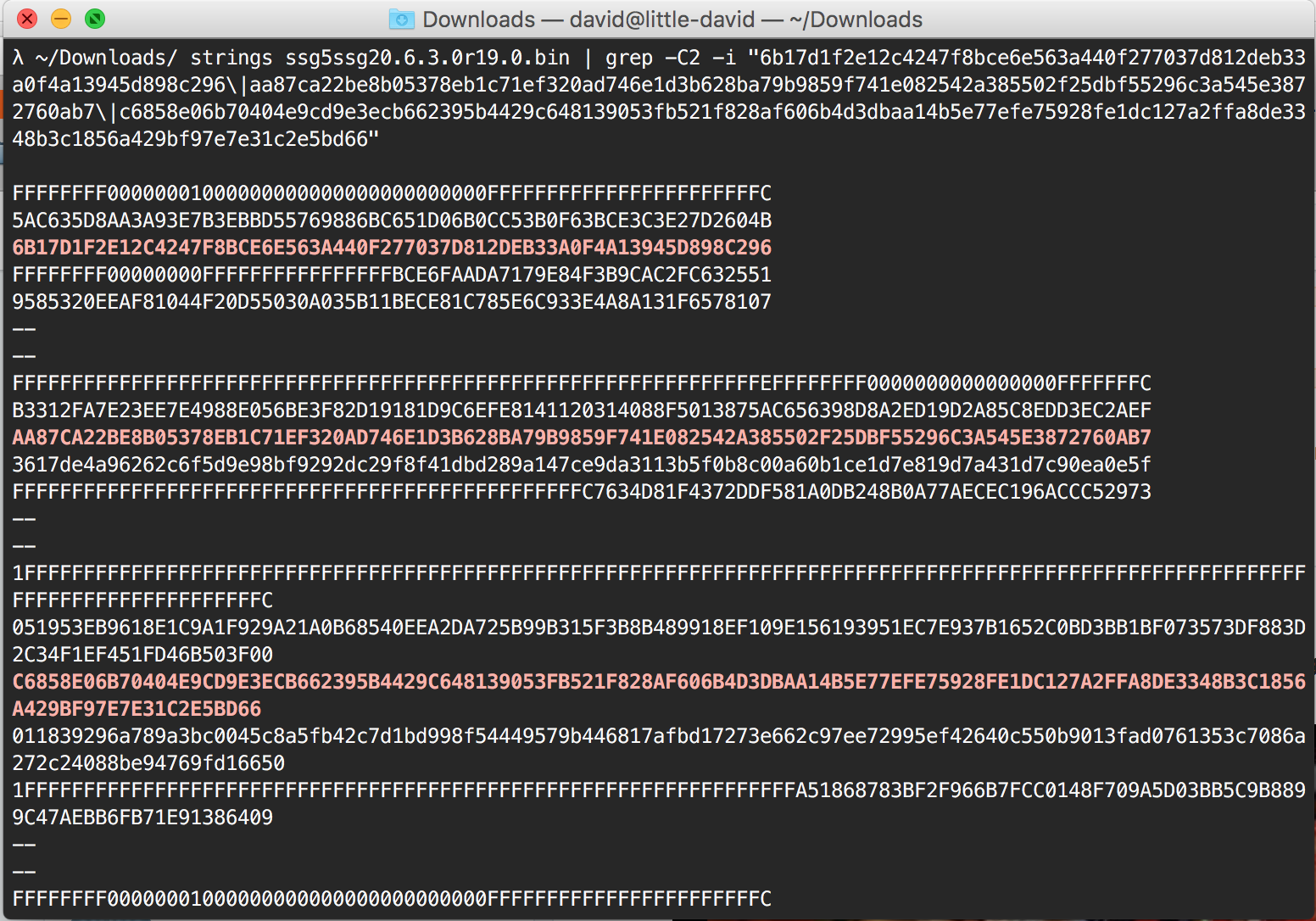
weirdly, testing for Qs I don't get any match. So Dual EC or not?

strings your_binary | grep -C5 -i "c97445f45cdef9f0d3e05e1e585fc297235b82b5be8ff3efca67c59852018192\|8e722de3125bddb05580164bfe20b8b432216a62926c57502ceede31c47816edd1e89769124179d0b695106428815065\|1b9fa3e518d683c6b65763694ac8efbaec6fab44f2276171a42726507dd08add4c3b3f4c1ebc5b1222ddba077f72943b24c3edfa0f85fe24d0c8c01591f0be6f63"

Re-reading CVE-2015-7765:

The Dual_EC_DRBG 'Q' parameter was replaced with 9585320EEAF81044F20D55030A035B11BECE81C785E6C933E4A8A131F6578107 and the secondary ANSI X.9.31 PRNG was broken, allowing raw Dual_EC output to be exposed to the network. Please see this blog post for more information.

Diffing the vulnerable (and patched binaries. I see that only the P-256 curve \(Q\) was modified from Juniper's values, other curves were left intact. I guess this means that only the P-256 curve was being used in Dual EC.

If you know how Dual EC works (if you don't check my video), you know that to establish a backdoor into it you need to generate \(P\) and \(Q\) accordingly. So changing the value \(Q\) with no correlation to \(P\) is not going to work, worse it could be that \(Q\) is too "close" to P and thus the secret \(d\) linking them could be easily found ( \(P = dQ \)).

Now one clever way to generate a secure \(Q\) with a strong value \(d\) that only you would know is to choose a large and random \(d\) and calculate its inverse \(d^{-1} \pmod{ord_{E}} \). You have your \(Q\) and your \(d\)!

\[ d^{-1} P = Q \]

bonus: here's a small script that attempts to find \(d\) in the hypothesis \(d\) would be small (the fastest way to compute an elliptic curve discrete log is to use Pollard Rho's algorithm)

p256 = 115792089210356248762697446949407573530086143415290314195533631308867097853951
a256 = p256 - 3
b256 =  41058363725152142129326129780047268409114441015993725554835256314039467401291

## base point values
gx = 48439561293906451759052585252797914202762949526041747995844080717082404635286
gy = 36134250956749795798585127919587881956611106672985015071877198253568414405109

## order of the curve
qq = 115792089210356248762697446949407573529996955224135760342422259061068512044369

# init curve
FF = GF(p256)
EE = EllipticCurve([FF(a256), FF(b256)]) 

# define the base point
G = EE(FF(gx), FF(gy)) 

# P and Q
P = EE(FF(0x6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296), FF(0x4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5))

# What is Q_y ?
fakeQ_x = FF(0x9585320EEAF81044F20D55030A035B11BECE81C785E6C933E4A8A131F6578107)
fakeQ = EE.lift_x(fakeQ_x)

print discrete_log(P, fakeQ, fakeQ.order(), operation='+')

The lift_x function allows me to get back the \(y\) coordinate of the new \(Q\):

EE.lift_x(fakeQ_x)
(67629950588023933528541229604710117449302072530149437760903126201748084457735 : 36302909024827150197051335911751453929694646558289630356143881318153389358554 : 1)