Byte ordering and bit numbering in Keccak and SHA-3 posted April 2017

As I talked about in a previous blogpost, Keccak and SHA3-3 are different in their bit convention, which gave birth to quite an overly complicated specification. The lack of good explanations in both the reference implementations and the reference documents led me to write this blogpost.

Padding

Before going further, let me briefly re-explain the multi-rate padding also called pad10*1:

1. take the input and append the delimiter (01 for SHA-3)
2. append a 1 to start the padding
3. append enough 0s followed by a final 1 so that the resulting output is a multiple of the rate

Here is a graphical example with input 0x9c = 1001 1100 and where the rate of our permutation is only 3 bytes:

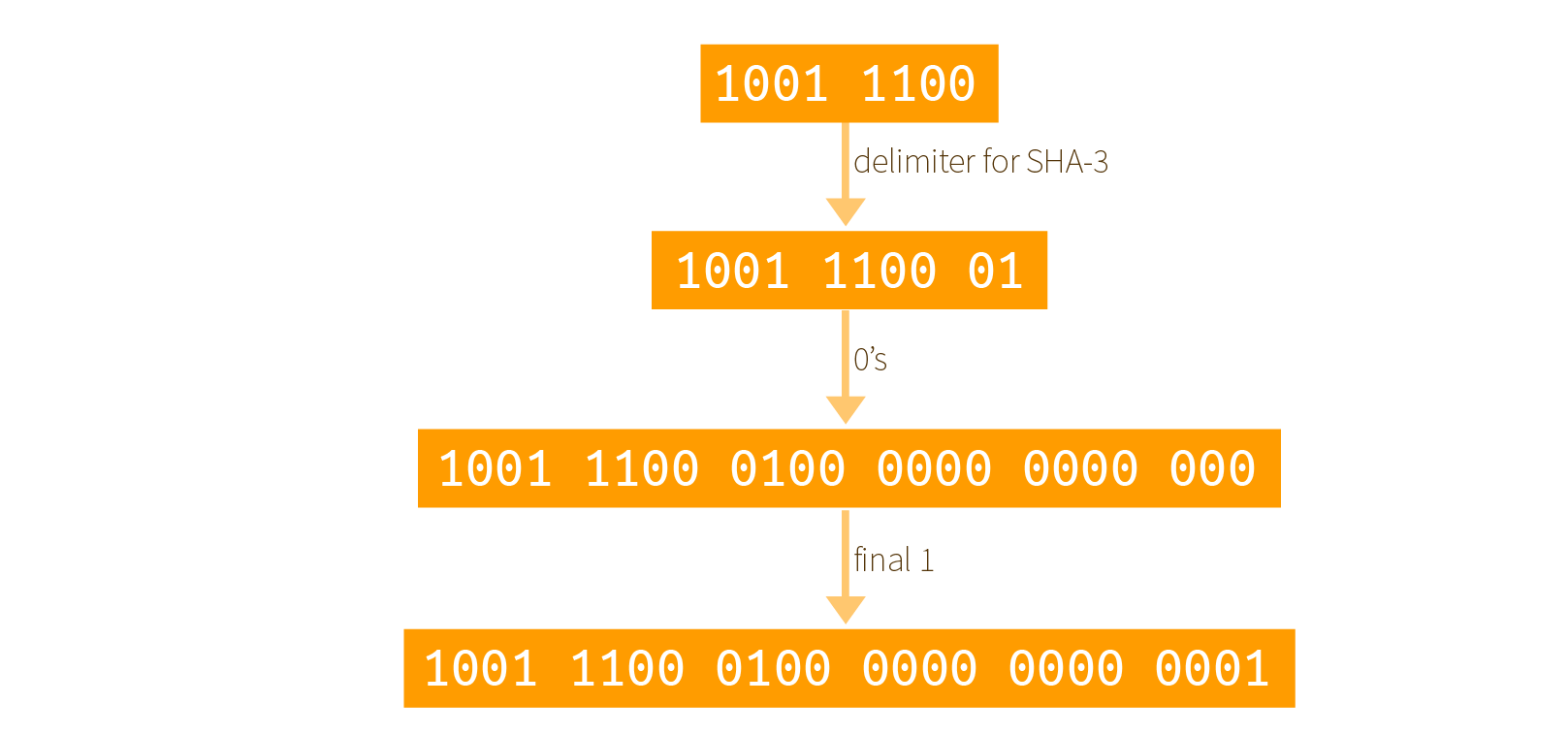
note that I forgot to add a 1 after the delimiter and before all the 0s (thanks Rachel)

Now, I'll just acknowledge that most implementations, and even the specification, talk about using 0x80 for the final bit. This blogpost should answer why.

Theoretical bit numbering

Keccak is specified in term of bits, but is discreetly aware of byte arrays as well. This is important as the rounds of Keccak require us to XOR parts of the input with lanes of the state. These lanes can be represented as uint64 types for keccak-f[1600], which we'll be looking at in this blogpost.

It could be hard to understand what is really going on in FIPS 202, but a look at an older version of the specification shows that Keccak interprets byte arrays in big-endian, but with an LSB bit numbering.

If you look at the Appendix B.1 of FIPS 202. You can see that before an input can be interpreted by SHA-3, it needs to go through some transformations.

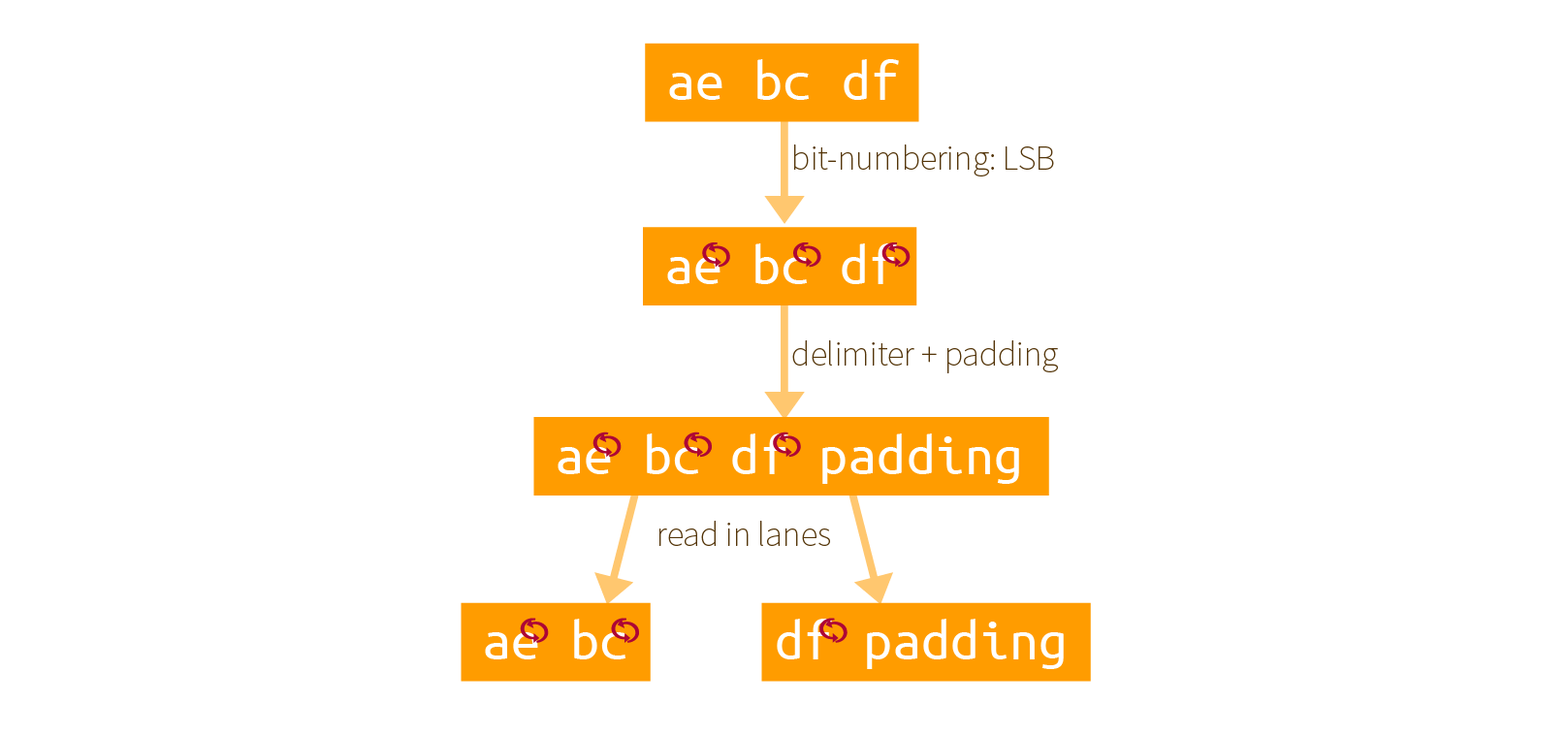
Here is our own example of how it works with an input of 0xaebcdf. First the bits are re-mapped, then a padding is added, finally it is split into as many lanes as possible (here we have two 16-bit lanes):

The same examples with bits:

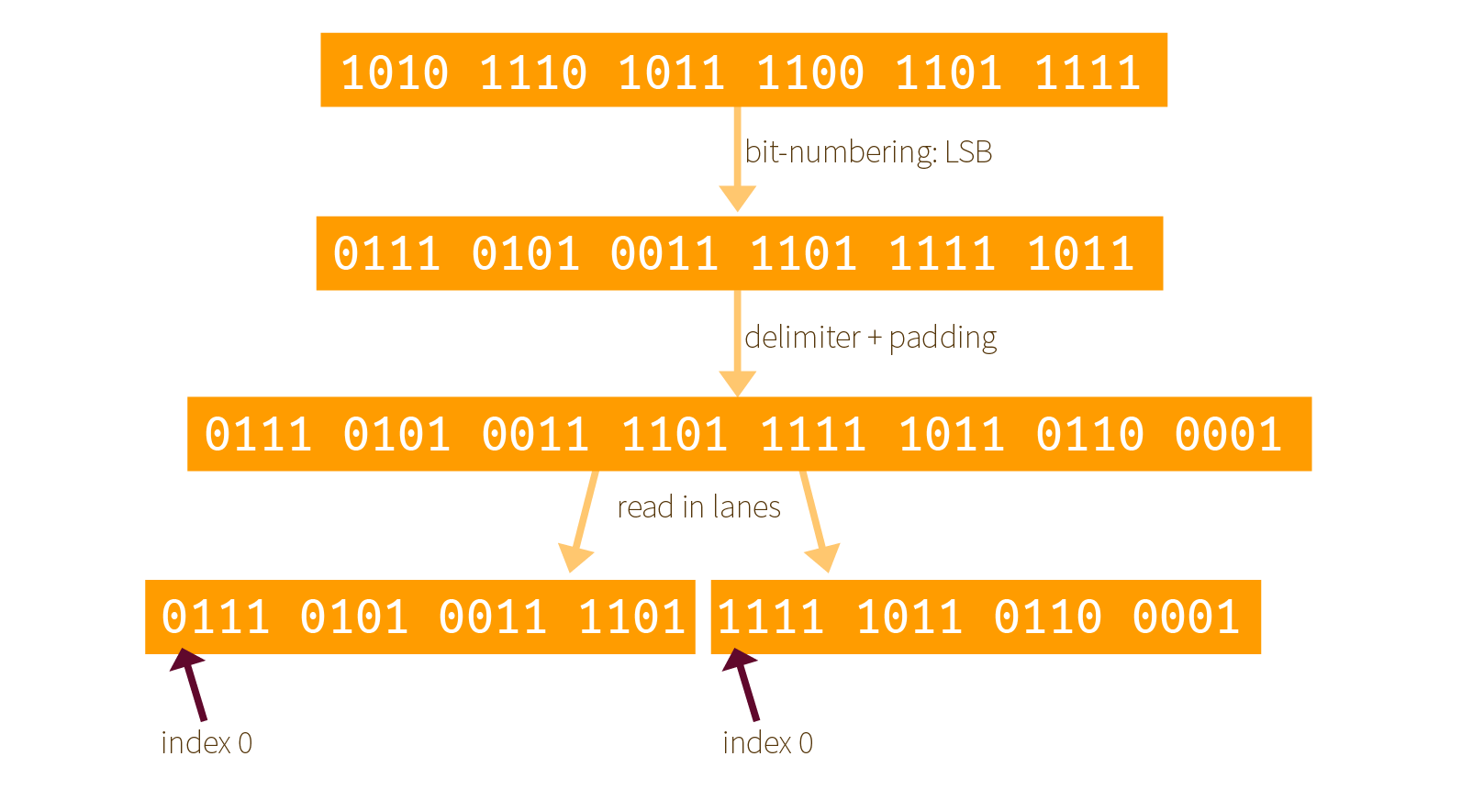
Two things that you must understand here:

• the padding is applied after re-mapping the bits, not before! Since the padding is already defined for Keccak's internal ordering of its bits.
• all of this is done so that a bit string is indexed as LSB first, not MSB first. It's weird but Keccak did it this way.

Why is the indexing of a bitstring so important?

Because we later apply the permutation function on the state, and some of the operations need to know what are the indexes of each bits. More on that later.

How to implement the re-mapping

It must be annoying to reverse all these bits right? What about not doing it? Well brace yourself, there is indeed a clever trick that would allow you to avoid doing this. And this trick is what is used in most of SHA-3's implementations. Here is a graphical explanation of what they do:

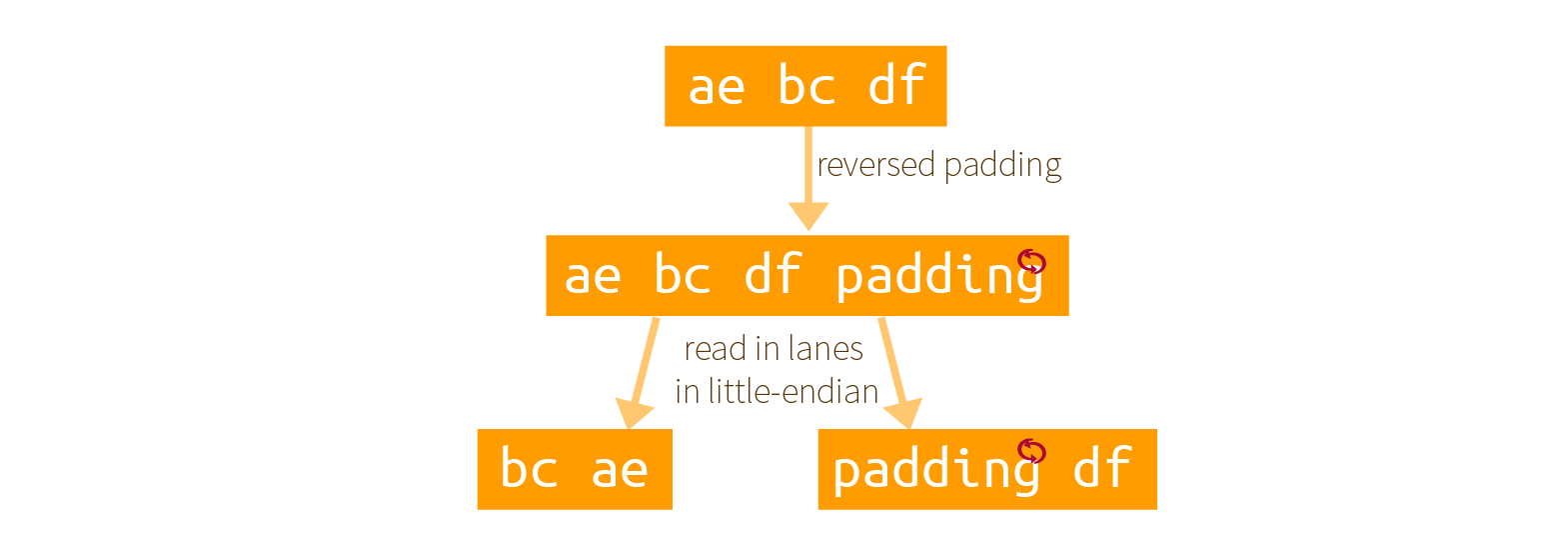
By reading the byte array as little-endian, and using an already reversed delimiter + padding, some magic happens!

The result is exactly the same but in reverse order.

If you aren't convinced look at the following diagram (which shows the same thing with bits) and look at the previous section result. Same, but the bitstream is readable in the reversed direction.

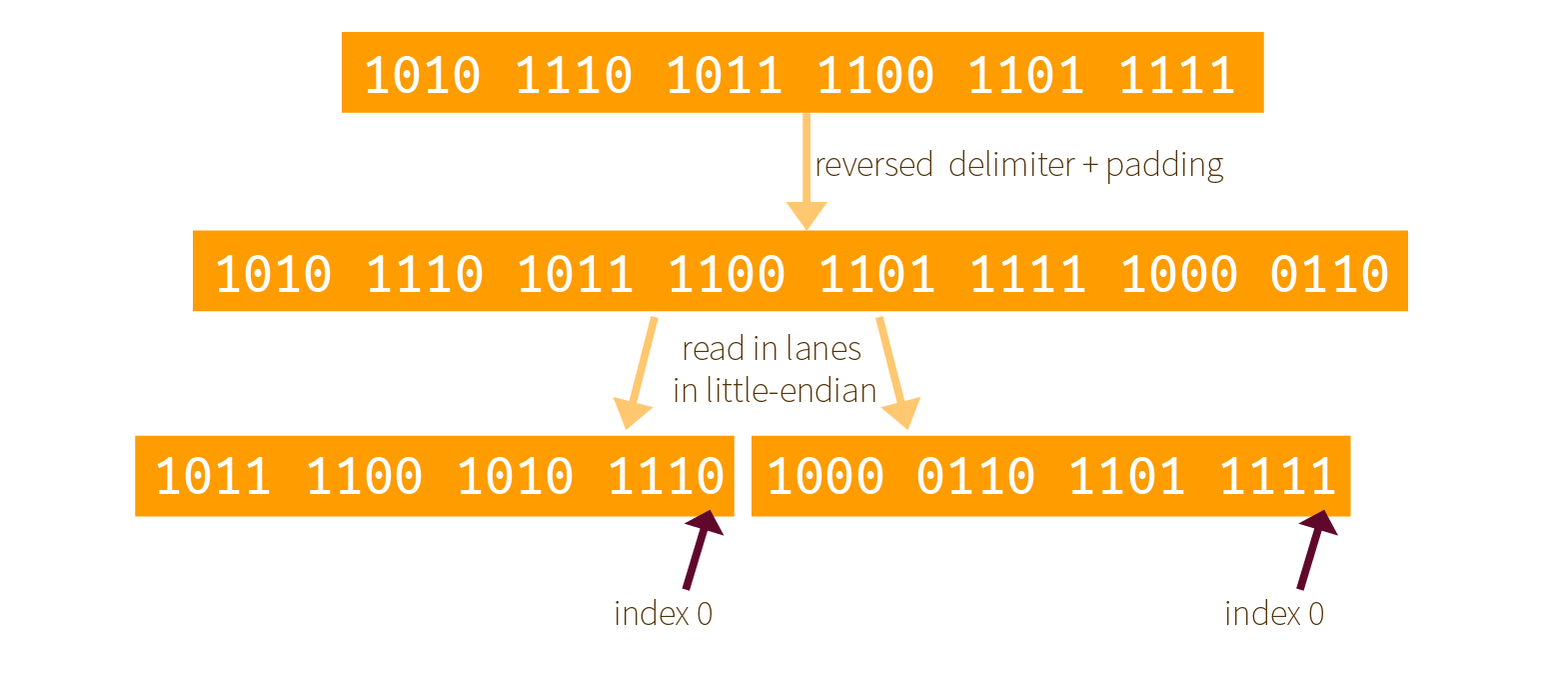
This means that now the index 0 of Keccak's internal ordering is on the right, not on the left. How will it influence the round functions that apply on our lanes?

It turns out that a lot of operations are unchanged. Who would have known that XORs, ANDs and NOTs operations were not affected by the order of the bits! but only some rotations and bit positioning are. If you look at the reference implementations you will see that indeed, rotations have been reversed (compared to what the reference tells you to do).

And this is how a clever implementation trick made its way in a specification with no real explanation.

You're welcome!