Updates on How to Backdoor Diffie-Hellman posted January 2018

Early in 2016, I published a whitepaper (here on eprint) on how to backdoor the Diffie-Hellman key agreement algorithm. Inside the whitepaper, I discussed three different ways to construct such a backdoor; two of these were considered nobody-but-us (NOBUS) backdoors.

A NOBUS backdoor is a backdoor accessible only to those who have the knowledge of some secret (a number, a passphrase, ...). Making a NOBUS backdoor irreversible without the knowledge of the secret.

In October 2016, Dorey et al. from Western University (Canada) published a white paper called Indiscreet Logs: Persistent Diffie-Hellman Backdoors in TLS. The research pointed out that one of my NOBUS construction was reversible, while the other NOBUS construction was more dangerous than expected.

I wrote this blogpost resuming their discoveries a long time ago, but never took the time to publish it here. In the rest of this post, I'll expect you to have an understanding of the two NOBUS backdoors introduced in my paper. You can find a summary of the ideas here as well.

Reversing the first NOBUS construction

For those who have attended my talk at Defcon, Toorcon or a meetup; I should assure you that I did not talk about the first (now-known reversible) NOBUS construction. It was left out of the story because it was not such a nice backdoor in the first place. Its security margins were weaker (at the time) compared to the second construction, and it was also harder to implement.

Baby-Step Giant-Step

The attack Dorey et al. wrote about comes from a 2005 white paper, where Coron et al. published an attack on a construction based on Diffie-Hellman. But before I can tell you about the attack, I need to refresh your memory on how the baby-step giant-step (BSGS) algorithm works.

Imagine that a generator \(g\) generates a group \(G\) in \(\mathbb{Z}_p\), and that we want to find the order of that group \(|G| = p_1\).

Now what we could do if we have a good idea of the size of that order \(p_1\), is to split that length in two right in the middle: \(p_1 = a + b \cdot 2^{\lceil \frac{l}{2} \rceil}\), where \( l \) is the bitlength of \(p_1\).

This allows us to write two different lists:

\[ \begin{cases} L = { g^i \mod{p} \mid 0 < i < 2^{\lceil \frac{l}{2} \rceil} } \\ L' = { g^{-j \cdot 2^{\lceil \frac{l}{2} \rceil} } \mod{p} \mid 0 \leq j < 2^{\lceil \frac{l}{2} \rceil} } \end{cases} \]

Now imagine that you compute these two lists, and that you then stumble upon a collision between elements from these two sets. This would entail that for some \(i\) and \(j\) you have:

\[ \begin{align} &g^i = g^{-j \cdot 2^{\lceil \frac{l}{2} \rceil}} \pmod{p}\\ \Leftrightarrow &g^{i + j \cdot 2^{\lceil \frac{l}{2} \rceil}} = 1 \pmod{p}\\ \Rightarrow &i + j \cdot 2^{\lceil \frac{l}{2} \rceil} = a + b \cdot 2^{\lceil \frac{l}{2} \rceil} = p_1 \end{align} \]

We found \(p_1\) in time quasi-linear (via sorting, searching trees, etc...) in \(\sqrt{p_1}\)!

The Construction

Now let's review our first NOBUS construction, detailed in section 4 of my paper.

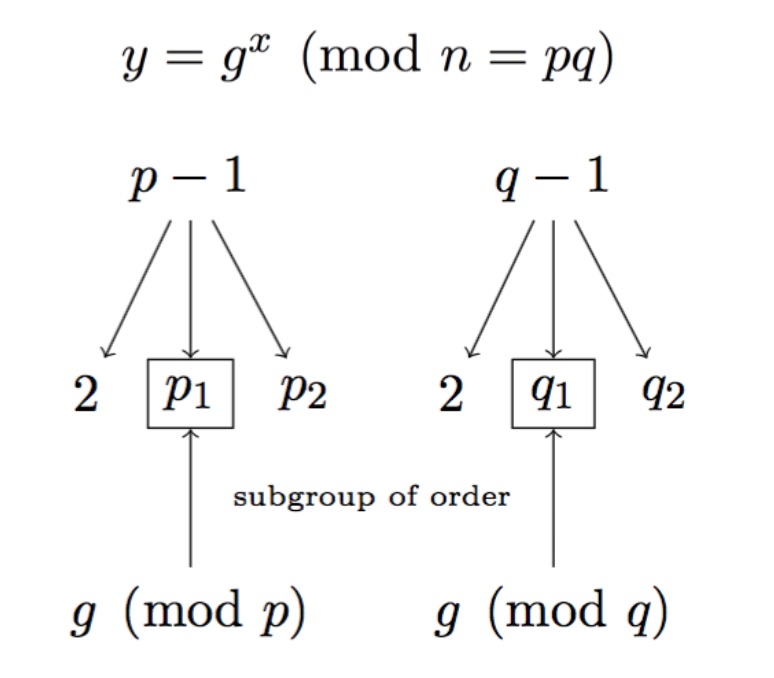
Here \(p - 1 = 2 p_1 p_2 \) with \( p_1 \) our small-enough subgroup generated by \(g\) in \(\mathbb{Z}_p\), and \(p_2\) our big-enough subgroup that makes the factorization of our modulus near-impossible. The factor \(q\) is generated in the same way.

Using BSGS on our construction

At this point, we could try to reverse the construction using BSGS by creating these two lists and hopping for a collision:

\[ \begin{cases} L = { g^i \mod{p} \mid 0 < i < 2^{\lceil \frac{l}{2} \rceil} } \\ L' = { g^{-j \cdot 2^{\lceil \frac{l}{2} \rceil} } \mod{p} \mid 0 \leq j < 2^{\lceil \frac{l}{2} \rceil} } \end{cases} \]

Unfortunately, remember that \(p\) is hidden inside of \( n = p q \). We have no knowledge of that factor. Instead, we could calculate these two lists:

\[ \begin{cases} L = { g^i \mod{n} \mid 0 < i < 2^{\lceil \frac{l}{2} \rceil} } \\ L' = { g^{-j \cdot 2^{\lceil \frac{l}{2} \rceil} } \mod{n} \mid 0 \leq j < 2^{\lceil \frac{l}{2} \rceil} } \end{cases} \]

And this time, we can test for a collision between two elements of these lists "mod \(p\)" via the \(gcd\) function:

\[ gcd(n, g^i - g^{-j \cdot 2^{\lceil \frac{l}{2} \rceil}}) \]

Hopefully this will yield \(p\), one of the factor of \(n\). If you do not understand why, it works because if \(g^i\) and \(g^{-j \cdot 2^{\lceil \frac{l}{2} \rceil}}\) collide "mod \(p\)", then we have:

\[ p | g^i - g^{-j \cdot 2^{\lceil \frac{l}{2} \rceil}} \]

Since we also know that \( p | n \), it results that the \(gcd\) of the two returns our hidden \(p\)!

Unfortunately at this point, the persnickety reader will have noticed that this cannot be done in the same complexity as the original BSGS attack. Indeed, we need to compute the \(gcd\) for all pairs and this increases our complexity to \(\mathcal{O}(p_1)\), the same complexity as the attack I pointed out in my paper.

The Attack

Now here is the that trick Coron et al. found out. They could optimize calls to \(gcd\) down to \(\mathcal{O}(\sqrt{p_1})\), which would make the reversing as easy as using the backdoor. The trick is as follow:

1. Create the polynomial

\[ f(x) = (x - g) (x - g^2) \cdots (x - g^{2^{\lceil \frac{l}{2} \rceil}}) \mod{n} \]

1. For \(0 \leq j < 2^{\lceil \frac{l}{2} \rceil}\) compute the following \(gcd\) until a factor of \(n\) is found (as before)

\[ gcd(n, f(g^{-j \cdot 2^{\lceil \frac{l}{2} \rceil}})) \]

It's pretty easy to see that the \(gcd\) will still yield a factor, as before. Except that this time we only need to call it at most \(2^{\lceil \frac{l}{2} \rceil}\) times, which is \(\approx \sqrt{p_1}\) times by definition.

Improving the second NOBUS construction

The second NOBUS backdoor construction received a different treatment. If you do not know how this backdoor works I urge you to first watch my talk on the subject.

Let's ask ourselves the question: what happens if the client and the server do not negotiate an ephemeral Diffie-Hellman key exchange, and instead use RSA or Elliptic Curve Diffie-Hellman to perform the key exchange?

This could be because the client did not list a DHE (ephemeral Diffie-Hellman) cipher suite in priority, or because the server decided to pick a different kind of key agreement algorithm.

If this is the case, we would observe an exchange that we could not spy on or tamper with via our DHE backdoor.

Dorey et al. discovered that an active man-in-the-middle could change that by tampering with the original client's ClientHello message to single-out a DHE cipher suite (removing the rest of the non-DHE cipher suites) and forcing the key exchange to happen by way of the Diffie-Hellman algorithm.

This works because there are no countermeasures in TLS 1.2 (or prior) to prevent this to happen.

Final notes

My original white paper has been updated to reflect Dorey et al.'s developments while minimally changing its structure (to retain chronology of the discoveries). You can obtain it here.

Furthermore, let me mention that the new version of TLS —TLS 1.3— will fix all of these issues in two ways:

• A server now signs the entire observed transcript at some point during the handshake. This successfully prevents any tampering with the ClientHello message as the client can verify the signature and make sure that no active man-in-the-middle has tampered with the handshake.
• Diffie-Hellman groups are now specified, exactly like how curves have always been specified for the Elliptic Curve variant of Diffie-Hellman. This means that unless you are in control of both the client and the server's implementations, you cannot force one or the other to use a backdoored group (unless you can backdoor one of the specified group, which is what happened with RFC 5114).