Quick access to articles on this page:
more on the next page...
The Web Public Key Infrastructure (PKI) is what's behind the green lock in your browser's URL bar. Actually, as I'm writing this, I realize that it's not even green anymore:

Now, instead of having a green lock that stands out, you get a "Not Secure" that stands out if you visit a non-HTTPS (or plain HTTP) website:

In this post I will briefly explain what this lock means, what the foundations for the security of the web are, and how blockchain technology can turn this into a better world.
The web PKI, in brief
When you talk to a website like Google, under the hood, your browser uses a protocol called TLS to secure the connection (and display the lock icon).
Part of that protocol is simply about making use of good old cryptography. Your browser performs a key exchange with Google's public key, and then encrypts the connection with some authenticated encryption algorithm. (If these words don't mean much to you, I introduce these concepts as well as TLS in my book Real-World Cryptography.)
The other part of the protocol is about identities. As in: "how can I trust that this secure connection I just established is really with Google?"
The only way we found out how to create trust between people's browsers and random websites on the web is by having a number of organizations manage these identities. These organizations are called "Certificate Authorities", and they are in charge of
verifying the owner of a domain (for example, google.com) before signing their public keys. The artifact they produce is usually referred to as a certificate.
Your browser trusts a number of these Certificate Authorities by default. They are hardcoded in the software you downloaded. When you connect to google.com, not only do you create a secure connection with some public key, but you also verify that this public key is signed by one of these Certificate Authorities that you trust.
Without this, you'd have to have all the public keys of all the websites on the internet baked in your browser. Not very practical.
This system, called the web PKI, is chaotic. Your browser ends up trusting hundreds of these authorities, and they sometimes misbehave (and sign certificates they should not):
When a Certificate Authorities misbehave, you sometimes have to revoke a number of the certificates they have signed. In other words, you need a way to tell browsers (or other types of clients) that the certificate they're seeing is no longer valid. This is another can of worms, as there is no list of all the current valid certificates that exists anywhere. You'd have to check with the Certificate Authority themselves if they've revoked the certificate (and if the Certificate Authority themselves has been banned... you'll need to update your browser).
Detecting attacks, Certificate Transparency to the rescue
To manage this insanity, Certificate Transparency (CT) was launched. An append-only log of certificates that relies on users (e.g. browsers) reporting what they see and gossiping between one another to make sure they see the same thing. Websites (like google.com) can use these logs to detect fraudulent certificates that were signed for their domains.
While Certificate Transparency has had some success, there are fundamental problems with it:
- it relies on clients (for example, browsers) to do the right thing and report what they see
- it is useful only to those who use it to monitor their domain (paranoids and large organizations who can afford security teams)
- it can only detect attacks, not prevent them
With the advance of blockchain-related technologies, we can take a different look at Certificate Transparency and notice that while it is very close to what a blockchain fundamentally is, it does not rely on a consensus protocol to ensure that everyone sees the same state.
Preventing attacks, blockchain to the rescue
If you think about it, a blockchain (touted as "a solution in search of a problem" by some technologists) solves exactly our scenario: it allows a set of organizations to police one another in order to maintain some updatable state. Here, the state is simply the association between websites and their public keys.
In this scenario, everyone sees the same state (there's consensus), and clients can simply own their state without going through a middle man (by being the first to register some domain name, for example).
There are many technical details to what I claim could be the web PKI 2.0. A few years back, someone could have simply retorted: "it'll be too slow, and energy inefficient, and browsers shouldn't have to synchronize to a blockchain".
But today, latest consensus systems like Bullshark and consensus-less systems like FastPay are not only green, but boast 125,000 and near-infinite transactions per second (respectively).
Not only that, but zero-knowledge proofs, as used in cryptocurrencies like Mina allow someone to receive a small proof (in the order of a few hundred bytes to a few hundred MB, depending on the zero-knowledge proof system) of the latest state of the blockchain. This would allow a browser to simply make a query to the system and obtain a short cryptographic proof that the public key they're seeing is indeed the one of google.com in the latest state.
Again, there are many details to such an implementation (how do you incentivize the set of participants to maintain such a system, who would be the participants, how do you prevent squatting, how do you prevent spam, etc.), but it'd be interesting to see if such a proof of concept can be realized in the next 5 years. Even more interesting: would such a system benefit from running on a cryptocurrency or would the alternative (in cryptocurrency lingo: a permissionned network based on a proof of authority) be fine?
In proof systems, provers and the verifiers rely on a common set of parameters, sometimes referred to as the common reference string (CRS).
In some proof systems (for example, the ones that rely on pairings) a dangerous setup phase produces these common parameters. Dangerous because it generates random values, encrypts them, and then must get rid of the random values so that no one can ever find out about them. The reason is that knowing these values would allow anyone to forge invalid proofs. Invalid proofs that verifiers would accept. Such values are sometimes referred to as toxic waste, and due to the fact that the individuals performing the setup have behave honestly, we call the setup a trusted setup.
By the way, since this common set of parameters has some hidden structure to it, it is usually referred to as structured reference string (SRS).
In the past, ceremonies (called powers of tau ceremonies) have been conducted where multiple participants collaborate to produce the SRS. Using cryptographic constructions called multi-party computations (MPC), the protocol is secure as long as one of the participant behaves honestly (and destroys the random values they generated as part of the ceremony).
It seems to be accepted in the community that such ceremonies are a pain to run. When mistakes happen, new ceremonies have to take place, which is what infamously happened to Zcash.
Some elliptic curves (related to zero-knowledge proofs I believe) have been claiming high 2-adicity. But for some reason, it seems a bit hard to find a definition of what this term means. And oddly, it's not a complicated thing to explain. So here's a short note about it.
You can see this being mentioned for example by the pasta curves:
They have the same 2-adicity, 32, unlike the Tweedle curves that had 2-adicity of 33 and 34. This simplifies implementations and may assist in square root performance (used for point decompression and internally to Halo 2) due to a new algorithm recently discovered; 32 is more convenient for this algorithm.
Looking at the definition of one of its field in Rust you can see that it is defined specifically for a trait related to FFTs:
impl FftParameters for FqParameters {
type BigInt = BigInteger;
const TWO_ADICITY: u32 = 32;
#[rustfmt::skip]
const TWO_ADIC_ROOT_OF_UNITY: BigInteger = BigInteger([
0x218077428c9942de, 0xcc49578921b60494, 0xac2e5d27b2efbee2, 0xb79fa897f2db056
]);
so what's that? Well, simply put, a two-adicity of 32 means that there's a multiplicative subgroup of size $2^{32}$ that exists in the field. And the code above also defines a generator $g$ for it, such that $g^{2^{32}} = 1$ and $g^i \neq 1$ for $i \in [[1, 2^{32}-1]]$ (so it's a primitive $2^{32}$-th root of unity).
Lagrange's theorem tells us that if we have a group of order $n$, then we'll have subgroups with orders dividing $n$. So in our case, we have subgroups with all the powers of 2, up to the 32-th power of 2.
To find any of these groups, it is pretty straight forward as well. Notice that:
- let $h = g^2$, then $h^{2^{31}} = g^{2^{32}} = 1$ and so $h$ generates a subgroup of order $2^31$
- let $h = g^{2^2}$, then $h^{2^{30}} = g^{2^{32}} = 1$ and so $h$ generates a subgroup of order $2^30$
- and so on...
In arkworks you can see how this is implemented:
let size = n.next_power_of_two() as u64;
let log_size_of_group = ark_std::log2(usize::try_from(size).expect("too large"));
omega = Self::TWO_ADIC_ROOT_OF_UNITY;
for _ in log_size_of_group..Self::TWO_ADICITY {
omega.square_in_place();
}
this allows you to easily find subgroups of different sizes of powers of 2, which is useful in zero-knowledge proof systems as FFT optimizations apply well on domains that are powers of 2. You can read more about that in the mina book.
Niall Murphy recently wrote about The Curse of Systems Thinkers (Part 1). In the post he made the point that some people (people who he calls "System thinkers" and who sound a lot like me to be honest) can become extremely frustrated by chaotic environments, and will seek to better engineer them as they engineer code.
He ends the post with a pessimistic take (which I disagree with):
If you can't get the ball rolling on even a small scale because no-one can see the need or will free-up the required resources, then you're free: they're fucked. Give yourself permission to let the organization fail
A while ago, Magoo suggested I read The Phoenix Project which is a book about engineering companies. Specifically, it's a novel that seeks to teach you lessons through an engaging story instead of a catalogue of bullet points. In the book, the analogy is made that any technology company is like an assembly line, and thus can be made efficient by using the lessons already learned decades ago by the manufacture industry.
The book also contains a side story about the failure of the security lead, which at the time really talked to me. The tl;dr is that the security person was too extreme (like all security engineers who have never worked on the other side) and could not recognize that the business needs were more urgent and more important than the security needs at the time. The security person was convinced to be right, and that the others didn't not care enough (reminiscent of Niall Murphy's blogpost), and consequently he lived a miserable life.
The point I'll be trying to make here is that it's all the same. Security, devops, engineering, ... it's all about trade offs and about finding what works well at a given time.
Ignoring yak shaving (which everyone does, and thus needs to be controlled), how much time and effort should be spent specifying protocols, documenting code, and communicating ideas? How much time and effort do we really need to spend writing clean code and refactoring?
I don't think there's a good or bad answer. The argument for both sides are strong:
Moving slow. Maintaining your own code, or having people maintain and extend your code, becomes harder and harder for the team with time. You will switch projects, and then go back to some code you haven't seen in a while. As the team grows, as people come and go, the situation amplifies as well. Obviously some people are better than others at reverse engineering code, but it's generally a hard problem.
Another argument is that some people on the team are not necessarily good programmers, or perhaps don't even know how to code, so it becomes hard/impossible for them to review or contribute in different ways. For example, by writing proofs with formal analysis tools or with a pen and paper, or to discuss the design with you, etc.
Complexity and rushed code obviously lead to security issues as well. That's undeniable.
Moving fast. On the other hand, you can't spend 90% of your time refactoring and doing things the_right_way™. You need to ship at some point. Business needs are often more important, and companies can go bankrupt by taking too much time to launch products. This is especially true during some stages of a company, in which it is in dire need of cash.
Furthermore, there are a ton of examples of companies growing massively while building on top of horrible stacks. Sometimes these companies can stagnate for years due to the amount of spaghetti code and complexity they're built on, and due to the fact that nobody is able to make changes effectively. But when this happens, codebases get rewritten from scratch anyway, which is not necessarily a bad thing. This is what happens with architecture, for example, where we tend to leave houses and buildings the way they are for very long periods of time, and destroy & rebuild when we really want to do consequent changes.
Eventually, the decision to move faster or slower is based on many factors. Many people work well in chaos and the system engineers might have to adapt to that.
That being said, extremes are always bad, and finding the right balance is always the right thing to do. But to find the right balance, you need extremists who will push and pull the company in different directions. Being a fanatic is a consuming job, and this is why you get a high turnover rate for such individuals (or blogposts like Niall Murphy telling you to let the organization fail).
This is the reason I personally left security.
The reasonable man adapts himself to the world; the unreasonable one persists in trying to adapt the world to himself. Therefore all progress depends on the unreasonable man.
-- George Bernard Shaw, Maxims for Revolutionists
This is a short note on the linearization step in Plonk (the zero-knowledge proof system), which is in my opinion the hardest step to understand.
Essentially, the linearization in Plonk exists due to two reasons:
- The polynomials we're dealing with are too big for the SRS (in the case of a polynomial commitment scheme, or PCS, like KZG) or URS (in the case of a PCS like bulletproof).
- During a proof verification, the verifier reconstructs the commitment to the polynomial that is aggregating all the constraints. To construct that commitment, the verifier adds commitments together, but must avoid multiplications as the commitment scheme used is only additively homomorphic.
Let's look at each of these in order.
The Reference String has a maximum size limit
The polynomials we're dealing with are too big for the SRS (in the case of a polynomial commitment scheme, or PCS, like KZG) or URS (in the case of a PCS like bulletproof).
Imagine that you have a polynomial with 4 coefficients:
$$
f = f_0 + f_1 x + f_2 x^2 + f_3 x^3
$$
Now imagine that your reference string is of size 2. This means that you can commit polynomials that have 2 coefficients max. The only way to commit to $f$ is to commit to the two polynomials with 2 or less coefficients separately:
- $com_1 = f_0 + f_1 x$
- $com_2 = f_2 + f_3 x$
Then, as part of the protocol, the prover evaluates this polynomial at some challenge point $\zeta$ and produces an evaluation proof for that. The verifier will have to first reconstruct the commitment to that polynomial, which can be constructed as:
$$
com = com_1 + \zeta^2 com_2
$$
Take a few minutes to understand why this works if needed.
Commitments are not homomorphic for the multiplication
During a proof verification, the verifier reconstructs the commitment to the polynomial that is aggregating all the constraints. To construct that commitment, the verifier adds commitments together, but must avoid multiplications as the commitment scheme used is only additively homomorphic.
Both the KZG and bulletproof PCS's use the Pedersen commitment, which is an homomorphic commitment scheme for the addition, but not for the multiplication. In other words, this means we can add commitments together (or add a commitment to itself many times), but not multiply commitments together.
So if $com_1$ is the commitment of the polynomial $g_1$ and $com_2$ is the commitment of the polynomial $g_2$. Then the following is fine:
$$
com_1 + com_2 = com(g_1 + g_2)
$$
While the following is not possible:
$$
com_1 \cdot com_2
$$
In this last case, the solution is to simply have the prover evaluate one of the commitments. For example, if we want to evaluate the polynomial (behind this commitment) to a challenge point $\zeta$, the prover could provide $g_1(\zeta)$ and the verfier would then compute the commitment of $g_1 \cdot g_2$ as
$$
g_1(\zeta) \cdot com_2
$$
This works, as long as the protocol uses this commitment to later verify an evaluation proof of $g_1(\zeta) \cdot g_2(\zeta)$.
Note that if $g_1$ is a polynomial that needs to remain private (part of the witness), then it should be blinded if you care about zero-knowledge.
As such, the linearization step of Plonk is a way to have the verifier construct a commitment as a linear combination of commitments. These commitments are generally preprocessed commitments contained in the verifier index (also called verifier key) or commitments that the verifier can generate themselves (the commitment to the public input polynomial for example).
I was at ZK Summit 7 in Amsterdam to talk about Kimchi (Mina's zero-knowledge proof system) with Joseph Spadavecchia.
https://youtu.be/n5FboUy3STY
I posted this on twitter initially, although it's short I think it's worthy of being reshared here.
The simplest abstraction is to see cryptocurrency / blockchain / distributed ledger technology as a database running on a single computer.
Everybody can access this database and there’s some simple logic that allows you to debit your account and credit someone else’s account.
The computer has a queue to make sure transactions are processed in order.
Blockchains that support smart contracts allow for people to install programs to that computer, which will add a bit more logic than simply debiting/crediting accounts. Others can then just send transactions to this computer to make a function call to any program (smart contract) that was installed on the computer.
The cool thing really is that we’re all using the same computer with the same database and the same programs.
Now in practice, nobody would trust a single point of failure like that. What if the computer crashes, or burns in a fire? Distributed systems to the rescue! We use distributed system protocols to run the same database on many computers distributed around the world.
These distributed system protocols effectively simulate a single database/computer so that a few computers failing doesn’t mean the end of the blockchain.
On top of that, we refuse to trust the computers that participate in this protocol. They could be lying about the balance in your account. We want the computers to police one another and agree on the database they are simulating.
That’s where consensus protocols are used: to make the distributed database secure even when some of the participants are malicious.
And that’s it. That’s blockchain tech for you. The obvious application is money, as the secure and simulated single computer is useful to simplify a payment system, but really any distributed database that cannot trust some of its participants can benefit from the advances there.
If you have questions about these analogies or other blockchain concepts, ask them in the comment section and I'll try to update this post :)
I initially posted this on https://minaprotocol.com/blog/kimchi-the-latest-update-to-minas-proof-system

(photo taken from https://unsplash.com/photos/M_mDgb8guhA)
We recently released an update to our proof system for Mina called Kimchi. Kimchi is the main machinery we use to generate the recursive proofs that allow the Mina blockchain to remain of a fixed size of 22KB. It will also soon enable privacy and local execution of smart contracts with our snapps update. In this post, we'll go through what Kimchi is and what's different about it.
First, it is good to see where in the stack we are. Looking at the edge of the network, what we can see is a big blackbox: Mina.

If you're curious enough, you can open it and see what's inside. At some point you'll end up with pickles. Pickles is the recursion layer, it is the protocol that we use to create proofs of proofs of proofs of ... and reduce the blockchain to a fixed-size of under 22KB.

Pickles need something to create proofs though, and this is what Kimchi is:
In this post, we'll attempt to create some abstractions and simplifications to teach intuitions about what Kimchi is. We will try to keep explanations at a relatively high level, so it will be up to you to open the blackboxes that we will lay before you.
One of these black boxes, for example, are the pasta curves.
There's clearly a theme here. All that's left is to change Mina's name to another pickled condiment.
A bit of context
Kimchi is based on PLONK, a proof system released in 2019 by Ariel Gabizon, Zachary J. Williamson, and Oana Ciobotaru. Since then, many ameliorations and extensions have been proposed. There's been fflonk, turbo PLONK, ultra PLONK, plonkup, and recently plonky2. It's hard to follow, but essentially all these protocols implement variants of PLONK. Thus, we call them plonkish protocols. Kimchi is such a plonkish protocol.
Today, PLONK is regarded as one of the most ambitious general-purpose zero-knowledge proof constructions. Many projects like Zcash, Polygon Zero (formerly known as Mir Protocol), Aztec network, Dusk, MatterLabs (zksync), Astar, and anoma, have their own implementation of the proof system.
But first, what is a proof system?
Let's look at a scenario that should shed some light on the construction's interface. If you understand this section, you're halfway there, as you'll be able to think for yourself on how general-purpose zero knowledge proofs can be used without having to figure out what's going on inside of it.
Let's imagine that Alice has a sudoku puzzle. She sends it to Bob, and Bob finds a solution to the puzzle. To prove it to her, he sends her the solution.
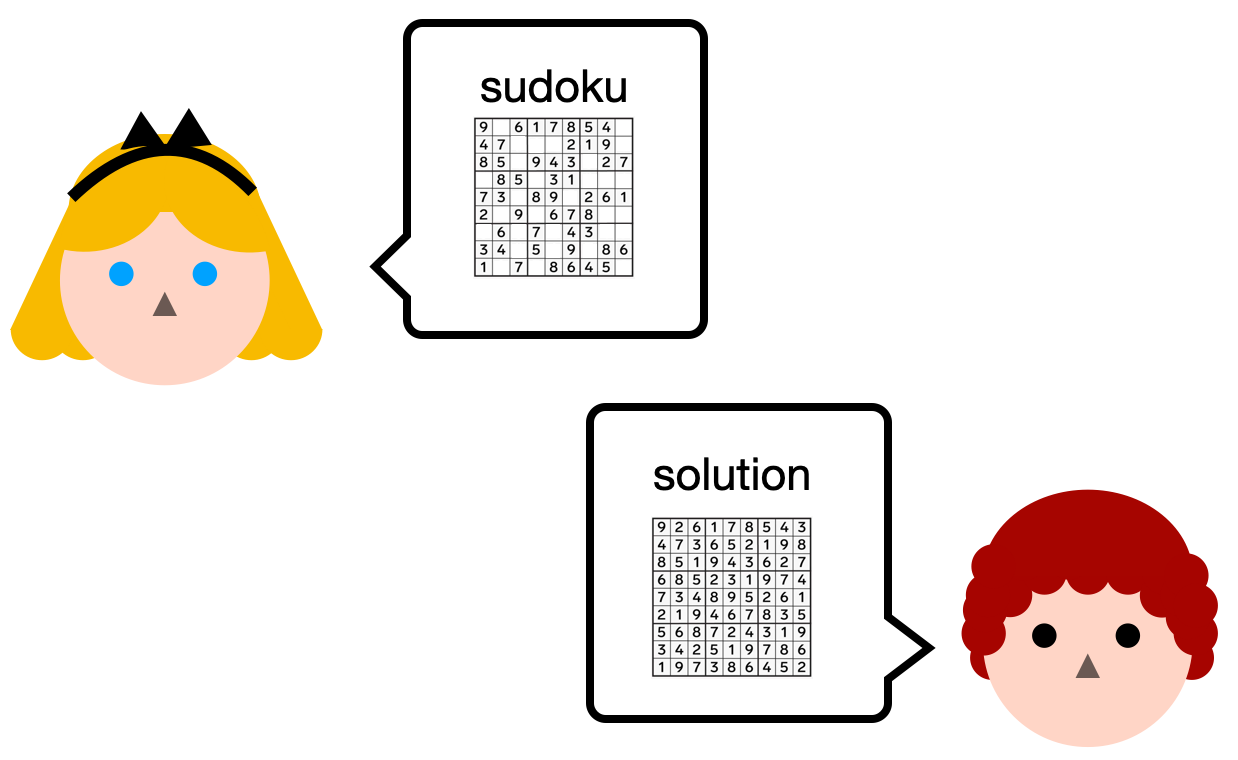
Alice can then run the solution, with the sudoku, in a program that will return true if the solution is correct.
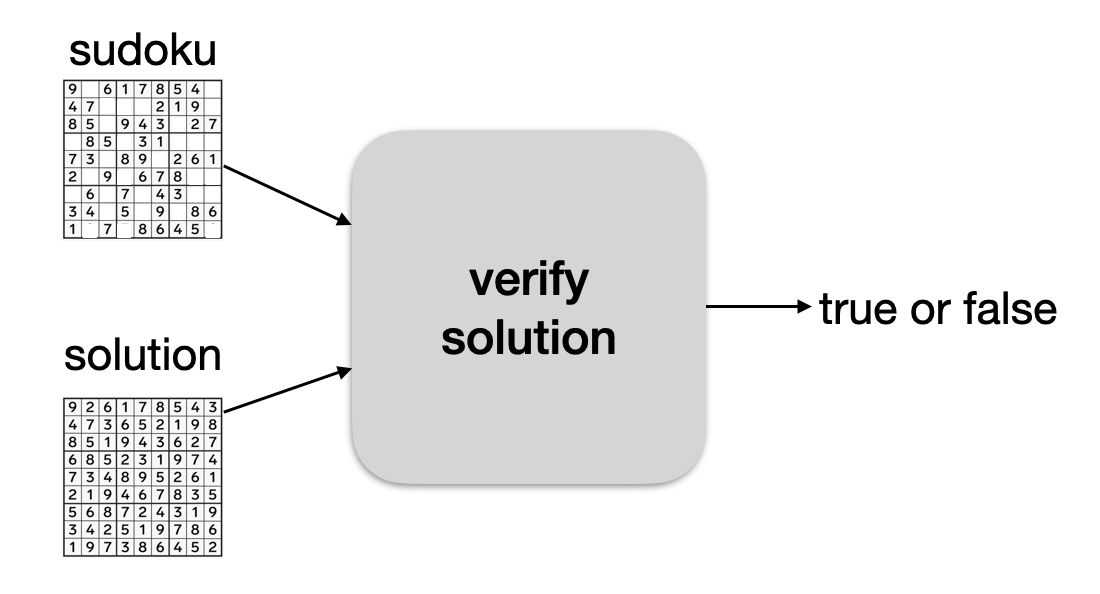
The problem is that Bob doesn't really want to share his solution... So instead, he runs the program himself, on his laptop, and tells Alice "I know a solution, trust me, I just ran the verify solution program on my laptop and it returned true".

Obviously Alice has no reason to trust Bob. We're in a bit of a pickle. This is where protocols like PLONK can be useful. The first step is to take our verify solution program in a special format (I'll come back to that later) and compile it down to two distinct blobs of data:
- the prover index (sometimes called the prover key, although it's not a real key)
- the verifier index (sometimes called the verifier key, not a key either)
Then the prover (Bob) can use a prove algorithm with the prover index, the sudoku puzzle, as well as his solution to execute the program and produce a proof of correct execution (a proof that the program returned true in this case).
We call the sudoku the public input, as it is known by others (like Alice), and the solution the private input, as Bob wants it to remain secret.
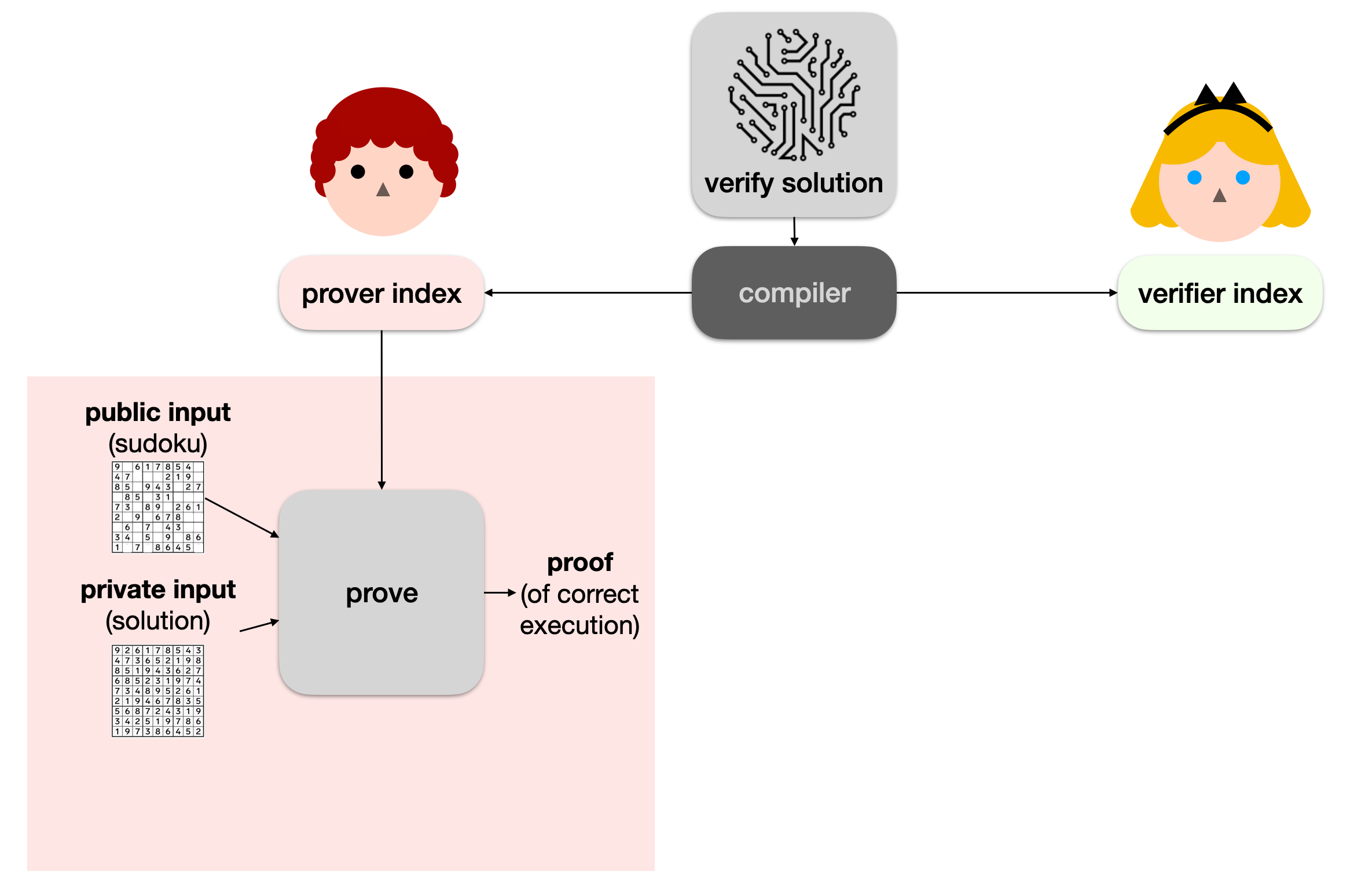
Note: here we don't really care about the output (we just want the program to correctly run to completion, which is equivalent to returning true). Sometimes though, we do care about having a public output (perhaps the result of the execution, which Alice can use). In these cases, the public output is part of the public input. (This detail doesn't really matter in practice.)
Now, Bob can simply give the proof to Alice, and Alice can verify it with another algorithm called verify. If the verify function returns true, she knows that Bob correctly ran the program verify solution to completion (using her sudoku puzzle and his solution).
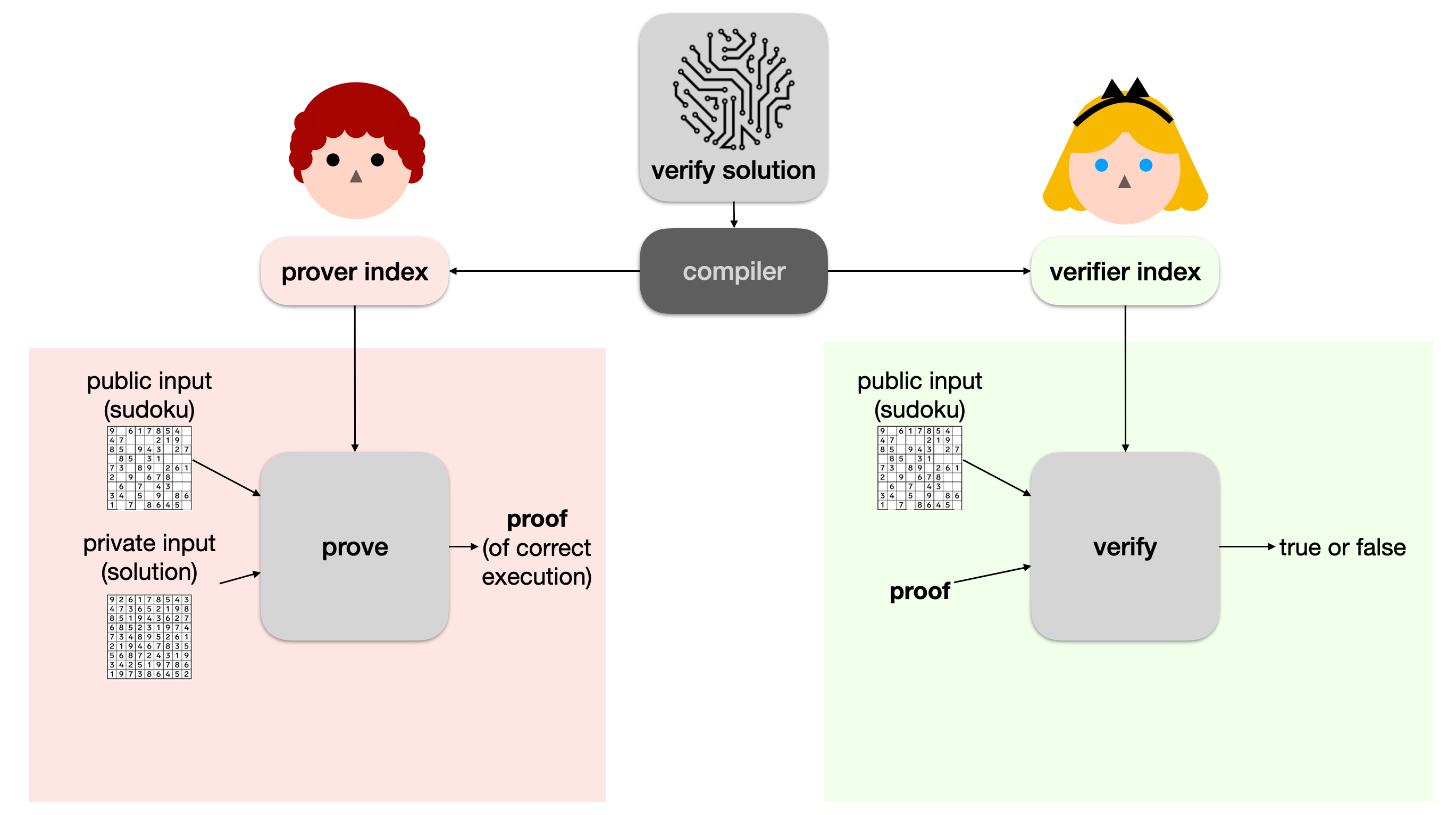
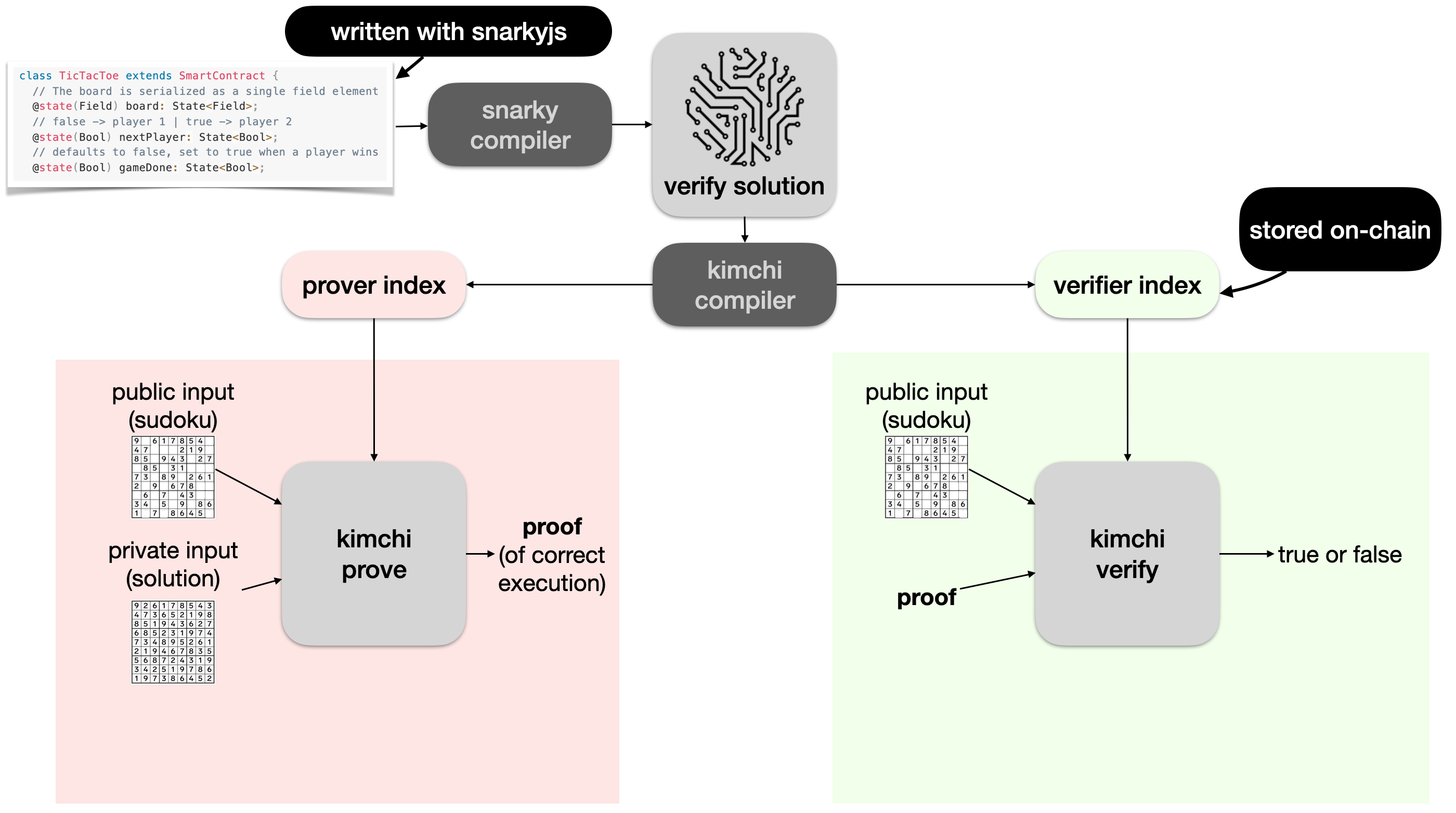
What about Snapps?
In Mina, snapps (zero-knowledge smart contracts) can be written in typescript using the snarkyjs library, and then compiled down to some intermediary representation with snarky. A Kimchi compiler can then be used to compile the program into the prover and verifier indexes, and both sides can use Kimchi provided functionalities to produce proofs as well as verify them.
The verifier index is uploaded on chain, which allows anyone to verify proofs contained in transactions that claim that they executed a snapp correctly.
Arithmetic circuits
Let's now address the elephant in the room: cryptography is about math and numbers, but programs like our sudoku solution verifier are about instructions and bits. That's not going to work. What can we do about it? The solution is to use arithmetic circuits!
Arithmetic circuits are circuits made out of arithmetic gates:
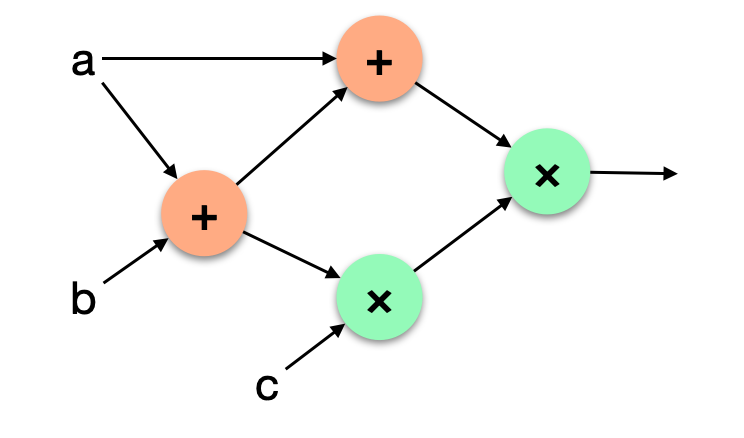
I'll argue that with an addition gate (that adds two numbers together) and a multiplication gate (that multiplies two numbers together) we can rewrite most programs.

Let's look at a simple example. Let's imagine that I want to use a bit x in a computation. To do that, I first need to make sure that x is indeed a bit (that it is 0 or 1).
Look at the following equation: x(x-1) = 0. This should be true, only if x is 0 or 1. We call that a constraint (we're constraining x to some values). Writing circuits for our proof system is about writing such constraints. Many of them in fact.
Let's see how that works with our arithmetic gates.
First we add 1 to -x (I'll explain how to get -x from x later). Then we use the multiplication gate with the output:

The output of the multiplication gate must be 0 (that's the constraint we want to write).
This is it, our circuit for now only has two gates. In PLONK, you would write this down as a list of gates acting on registers (the two inputs L and R, and the output O):
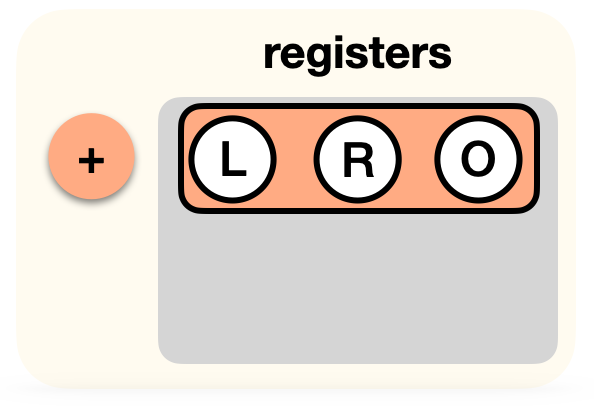
Now, we aren't really doing an addition of L and R here, we're rather adding 1 to -R. How do we do this? Perhaps we could have a "add with constant" gate, and a "subtract gate"? Instead, we "tweak" our addition gate:
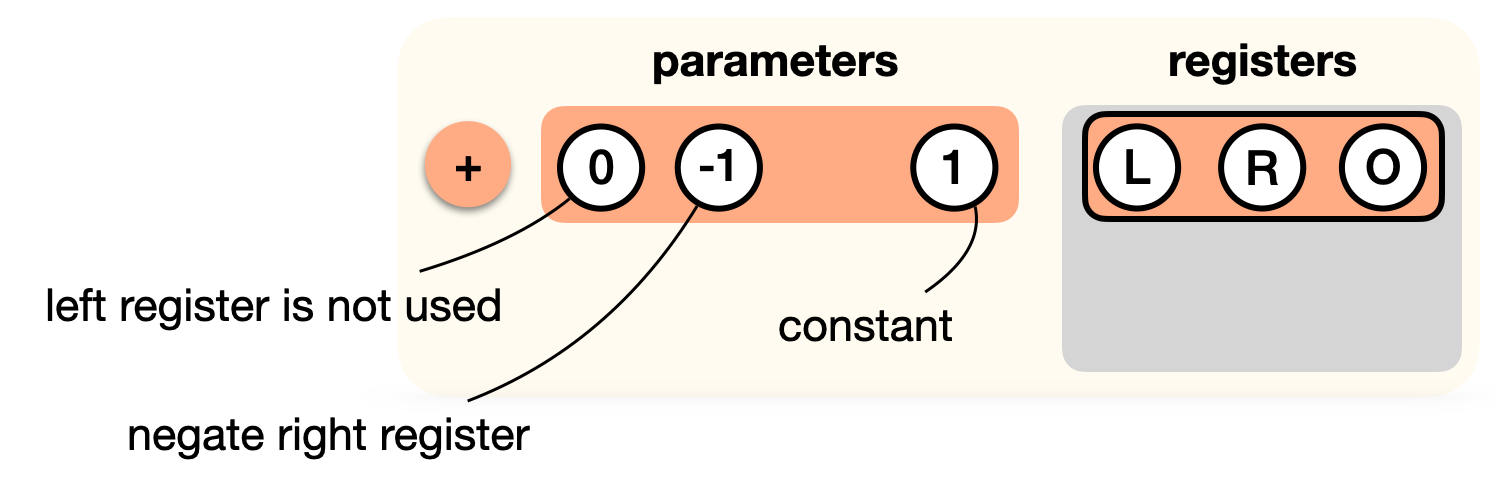
Now let's add the multiplication gate to the list. But remember, the output register is not used, as it must be 0. So we tweak that gate as well:
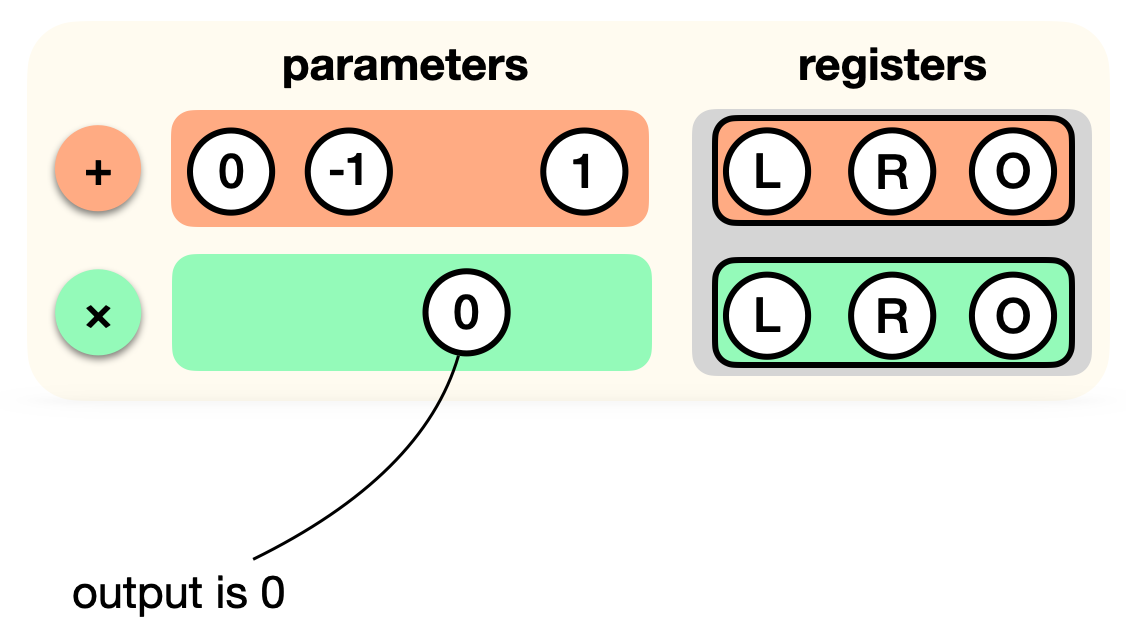
More on tweaking these gates later.
There's one last thing that we're missing: the output register of the first gate is the left register of the second gate. We can simply wire the two registers to encode this correspondance:
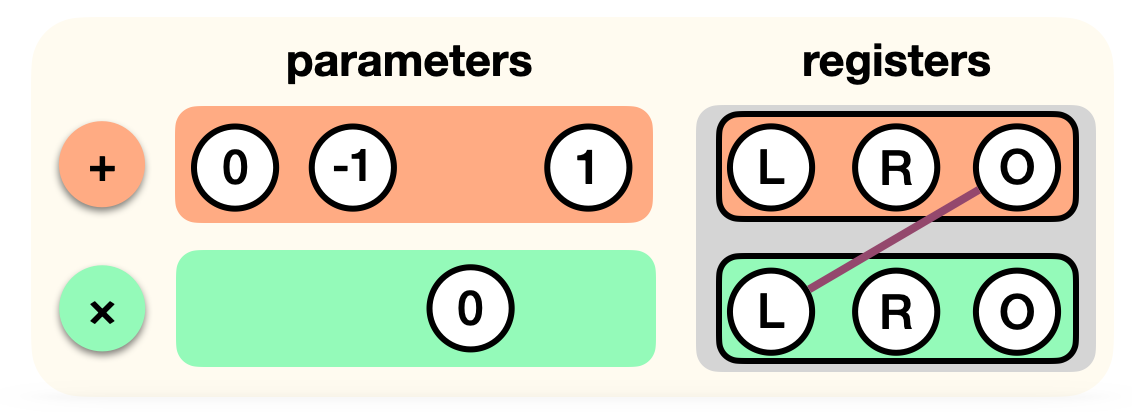
And this is how we represent a circuit in PLONK! We just list all the gates (and their parameters) as well as the wiring between the registers they act on.
Now, when a prover wants to produce a proof, they will run the program and record the values of each registers in an execution trace. For example, here is one that takes x = 0.
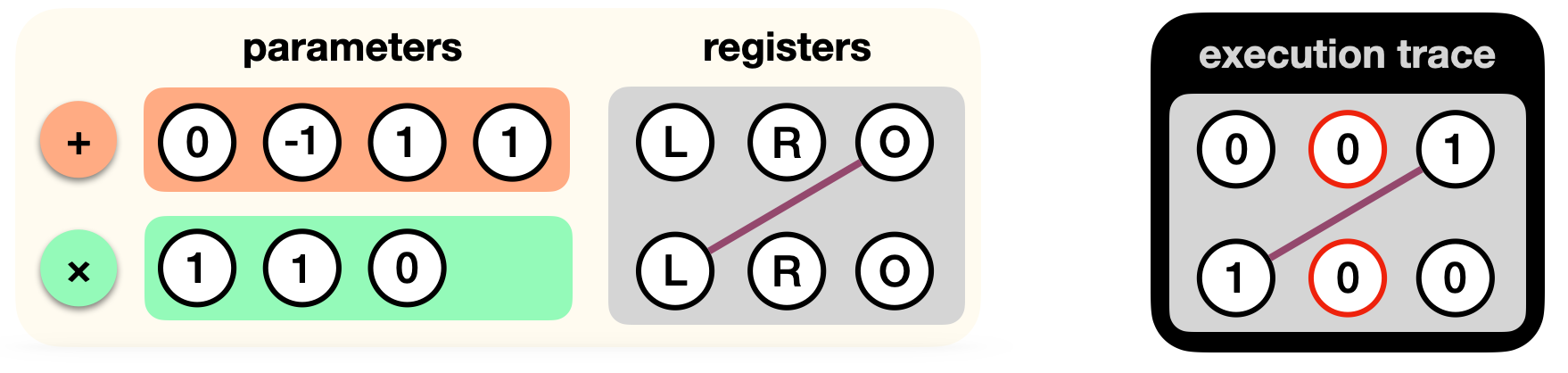
Note: the values in the left register of the first gate, and the output register of the second gate, can be anything as they are not used by the gates.
One simplification I made, is that we don't know where x comes from here. In a real circuit, the right registers of this execution trace are wired to another register containing the value x (or perhaps it is given as private or public input to the circuit, but I will avoid explaining how this works here).
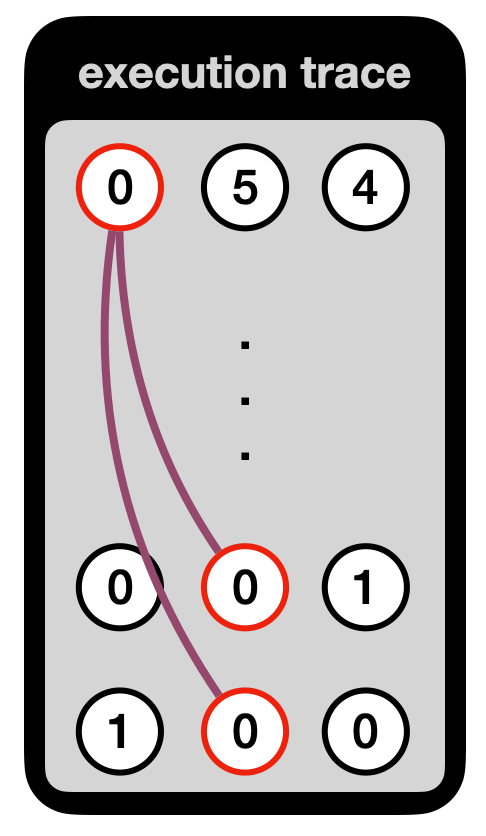
Another simplification I made, is that in reality the addition and multiplication gates are implemented as a single tweakable gate that we call the generic gate in Kimchi:
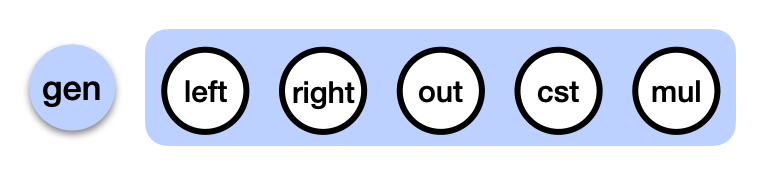
Tweaking the parameters of the generic gate essentially turns it into different gates (addition, multiplication, addition with constant, subtraction, etc.)

From PLONK to Kimchi
Kimchi is a collection of improvements, optimizations, and alterations made on top of PLONK. For example, it overcomes the trusted setup limitation of PLONK by using a bulletproof-style polynomial commitment inside of the protocol. This way, there is no need to trust that the participants of the trusted setup were honest (if they were not, they could break the protocol). Talking about circuits, since we're talking about circuits here, Kimchi adds 12 registers to the 3 registers PLONK already had:

These registers are split into two types of registers: the IO registers, which can be wired to one another, and temporary registers (sometimes called advice wires) that can be used only by the associated gate.
More registers means that we now can have gates that take multiple inputs instead of just one:
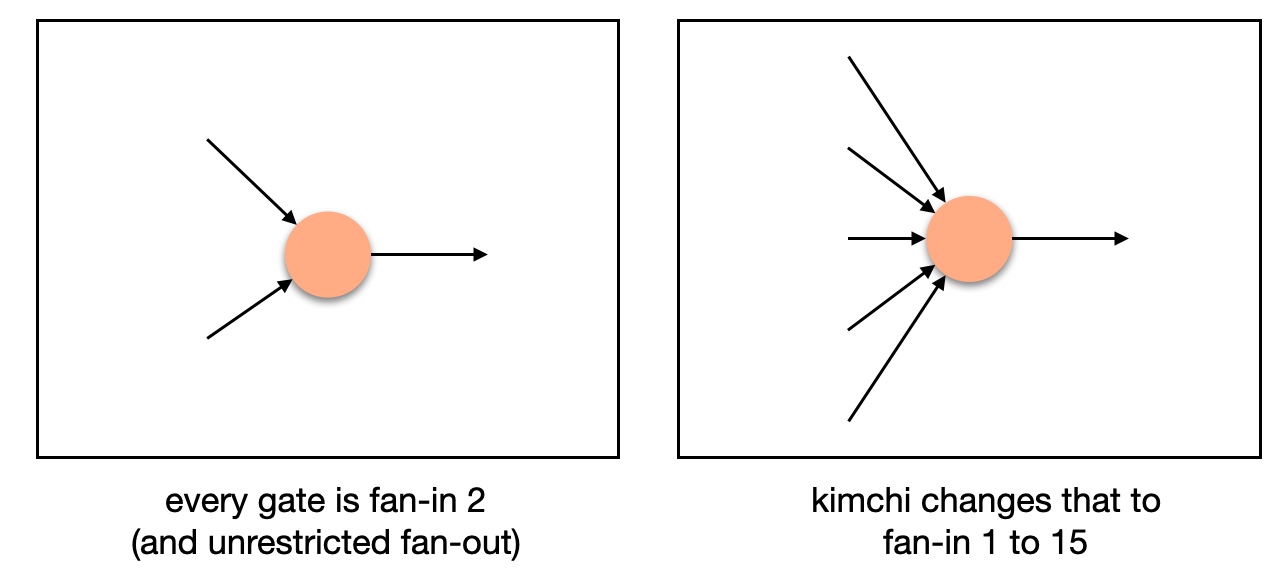
This opens new possibilities. For example, a scalar multiplication gate would require at least three inputs (a scalar, and two coordinates for the curve point). As some operations happen more often than others, they can be rewritten more efficiently as new gates. Kimchi offers 9 new gates at the moment of this writing:

Another concept in Kimchi is that a gate can directly write its output on the registers used by the next gate. This is useful in gates like "poseidon", which need to be used several times in a row (11 times, specifically) to represent the poseidon hash function:

Another performance improvement implemented in Kimchi are lookups. Sometimes, some operations can be written as a table. For example, an XOR table:
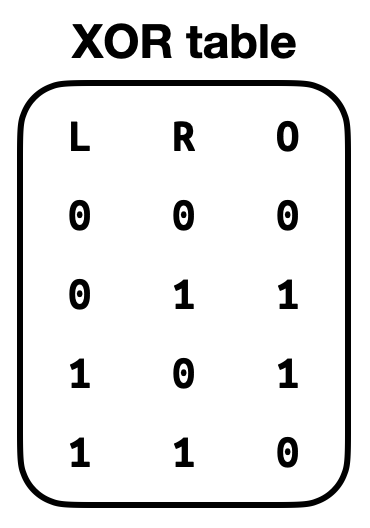
An XOR table for values of 4 bits is of size 28. Implementing this with generic gates would be hard and lengthy, so instead Kimchi builds the table and allows gates (so far only Chacha uses it) to simply perform a lookup into the table to fetch for the result of the operation.
There's much more to Kimchi, but this is for another time. You can check out the implementation here and if you're curious opening the other blackboxes you can check our our in-depth explanations here.
To summarize
Pickles now uses an upgraded proof system: Kimchi. Kimchi brings several optimizations and quality-of-life improvements to circuit builders. This should allow for faster provers, larger circuits, and potentially shorter proof sizes!































