Small RSA private key problem posted April 2015

/!\ this page uses LaTeX, if you do not see this: \( \LaTeX \)

then refresh the page

Plaid CTF

The third crypto challenge of the Plaid CTF was a bunch of RSA triplet \( N : e : c \) with \( N \) the modulus, \( e \) the public exponent and \( c \) the ciphertext.

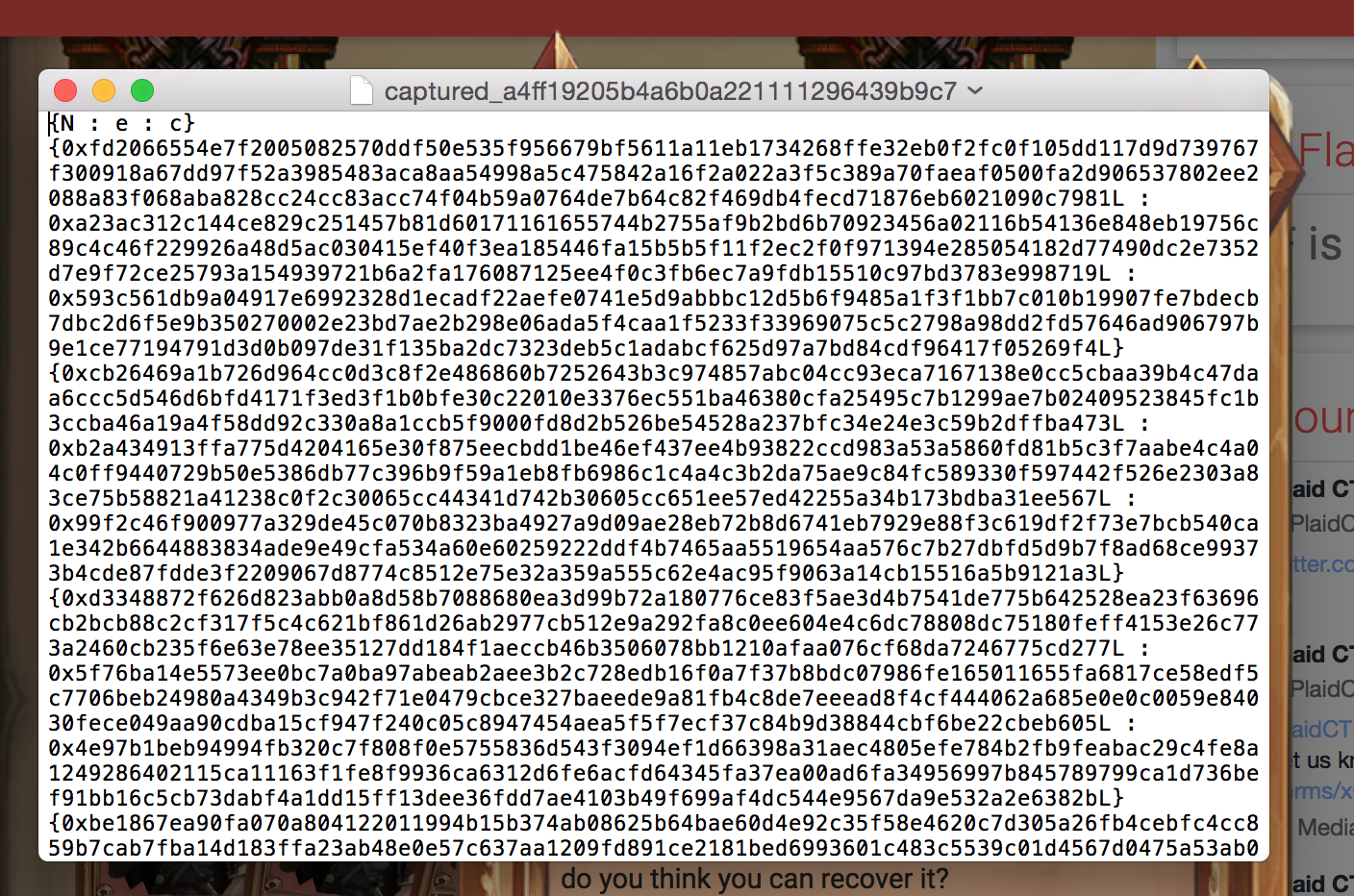
The public exponents \( e \) are all pretty big, which doesn't mean anything in particular. If you look at RSA's implementation you often see \( 3 \), \( 17 \) or other Fermat primes (\( 2^m + 1 \)) because it speeds up calculations. But such small exponents are not forced on you and it's really up to you to decide how big you want your public exponent to be.

But the hint here is that the public exponents are chosen at random. This is not good. When you choose a public exponent you should be careful, it has to be coprime with \( \varphi(N) \) so that it is invertible (that's why it is always odd) and its related private exponent \( d \) shouldn't be too small.

Maybe one of these public keys are associated to a small private key?

I quickly try my code on a small VM but it takes too much time and I give up.

Wiener

A few days after the CTF is over, I check some write-ups and I see that it was indeed a small private key problem. The funny thing is that they all used Wiener to solve the challenge.

Since Wiener's algorithm is pretty old, it only solves for private exponents \( d < N^{0.25} \). I thought I could give my code a second try but this time using a more powerful machine. I use this implementation of Boneh and Durfee, which is pretty much Wiener's method but with Lattices and it works on higher values of \( d \). That means that if the private key was bigger, these folks would not have found the solution. Boneh and Durfee's method allows to find values of private key up to \( d < N^{0.292} \)!

After running the code (on my new work machine) for 188 seconds (~ 3 minutes) I found the solution :)

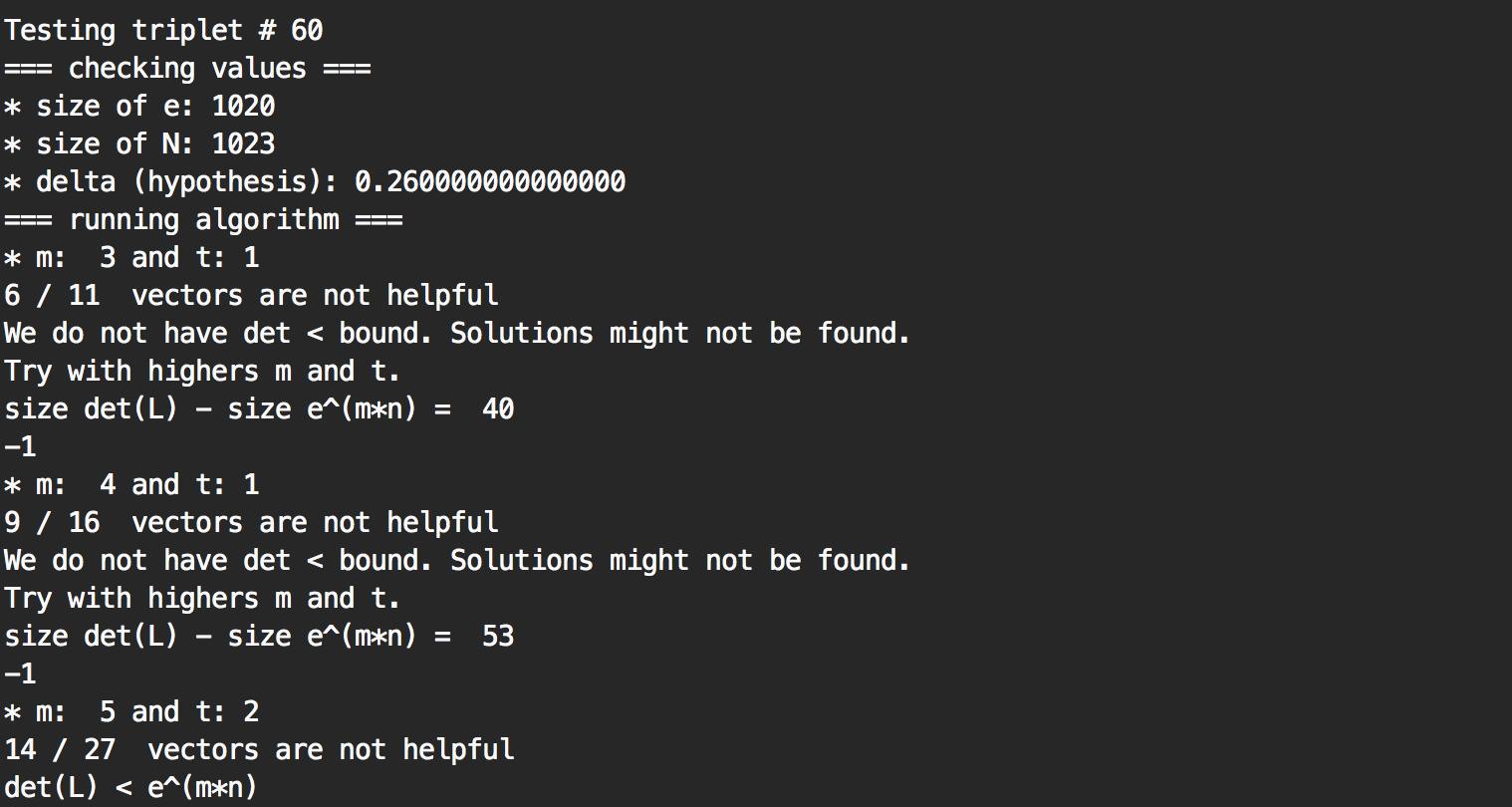
Here we can see that a solution was found at the triplet #60, and that it took several time to figure out the correct size of lattice (the values of \( m \) and \( t \)) so that if there was a private exponent \( d < N^{0.26} \) a solution could be found.

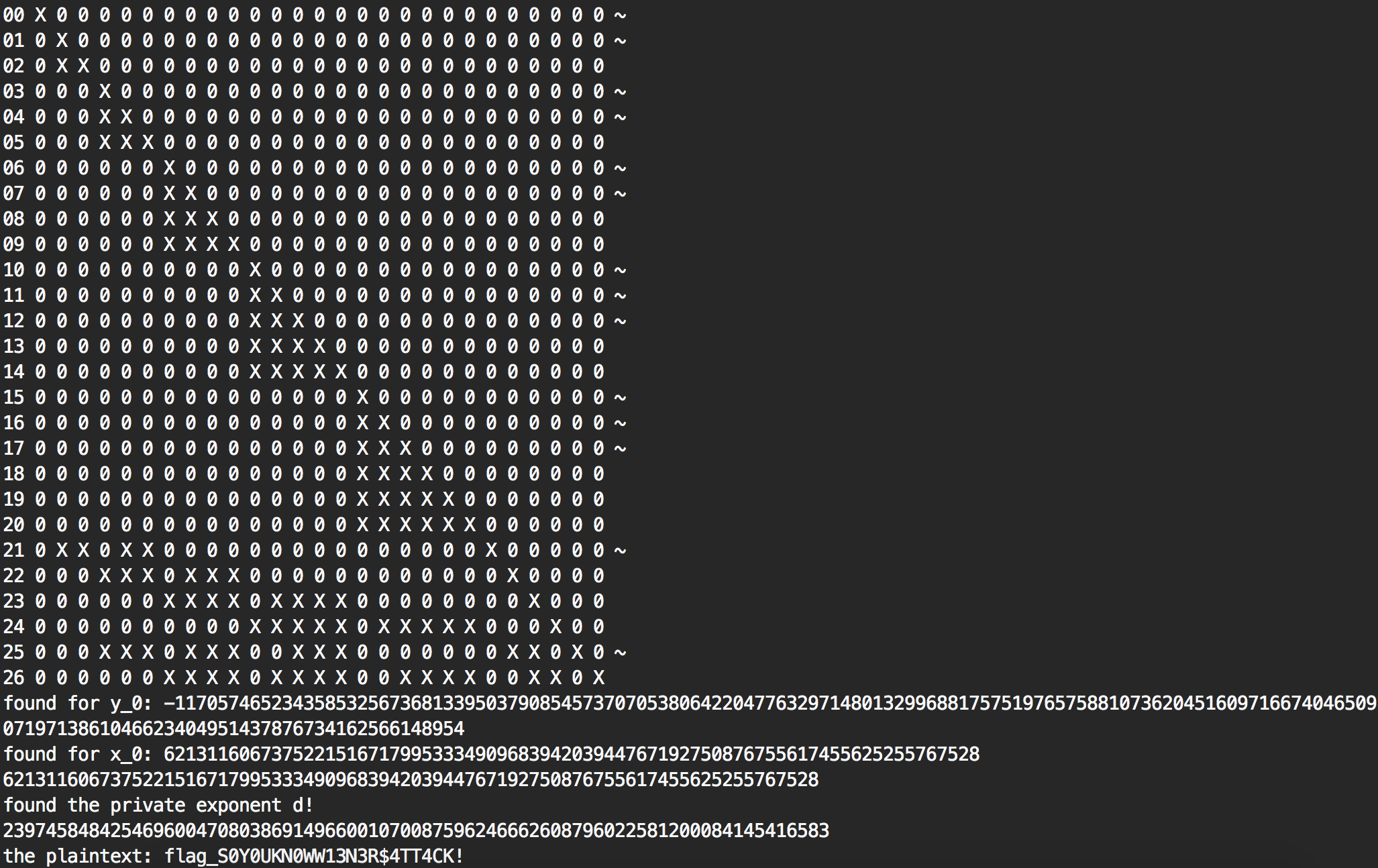
The lattice basis is shown as a matrix (the ~ represents an unhelpful vector, to try getting rid of them you can use the research branch), and the solution is displayed.

Boneh and Durfee

Here is the code if you want to try it. What I did is that I started with an hypothesis \( delta = 0.26 \) which tested for every RSA triplets if there was a private key \( d < N^{0.26 } \). It worked, but if it didn't I would have had to re-run the code for \(delta = 0.27\), \(0.28\), etc...

I setup the problem:

# data is our set of RSA triplets
for index, triplet in enumerate(data):

    print "Testing triplet #", index

    N = triplet[0]
    e = triplet[1]

    # Problem put in equation
    P.<x,y> = PolynomialRing(ZZ)
    A = int((N+1)/2)
    pol = 1 + x * (A + y)

I leave the default values and set my hypothesis:

delta = 0.26
X = 2*floor(N^delta)
Y = floor(N^(1/2))

I use strict = true so that if the algorithm will stop if a solution is not sure to be found. Then I increase the values of \( m \) and \( t \) (which increases the size of our lattice) and try again:

solx = -1
m = 2
while solx == -1:
    m += 1
    t = int((1-2*delta) * m)  # optimization from Herrmann and May
    print "* m: ", m, "and t:", t
    solx, soly = boneh_durfee(pol, e, m, t, X, Y)

If no private key lesser than \(N^{delta}\) exists, I try the next triplet. However, if a solution is found, I stop everything and display it.

Remember our initial equation:

\[ e \cdot d = f(x, y) \]

And what we found are \(x\) and \(y\)

if solx != 0:
    d = int(pol(solx, soly) / e)
    print "found the private exponent d!"
    print d

    m = power_mod(triplet[2], d, N)
    hex_string = "%x" % m
    import binascii
    print "the plaintext:", binascii.unhexlify(hex_string)

    break

And that's it!

More?

If you don't really know about lattices, I bet it was hard to follow. But do not fear! I made a video explaining the basics and a survey of Coppersmith and Boneh & Durfee

Also go here and click on the follow button.