Some research on recovering small RSA private keys posted April 2015

To make it short, I did some research on the Boneh and Durfee bound, made some code and it worked. (The bound that allows you to find private keys if they are lesser than \(N^{0.292}\))

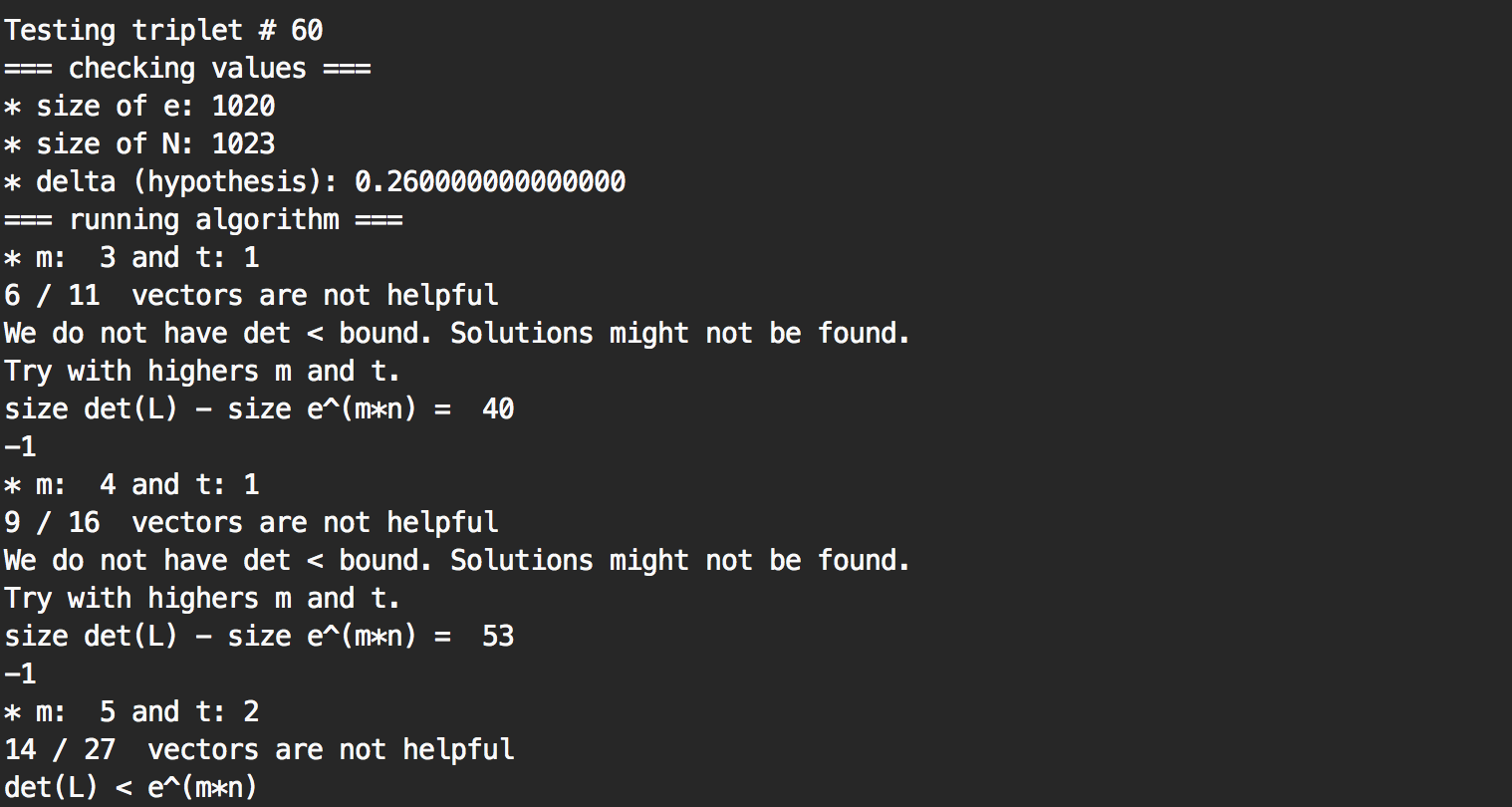
I noticed that many times, the lattice was imperfect as many vectors were unhelpful. I figured I could try to remove those and preserve a triangular basis, and I went even further, I removed some helpful vectors when they were annoying. The code is pretty straightforward (compare to the boneh and durfee algorithm here)

So what happens is that I make the lattice smaller, so when I feed it to the lattice reduction algorithm LLL it takes less time, and since the complexity of the whole attack is dominated by LLL, the whole attack takes less time.

It was all just theoric until I had to try the code on the plaid ctf challenge. There I used the normal code and solved it in ~3 minutes. Then I wondered, why not try running the same program but with the research branch?

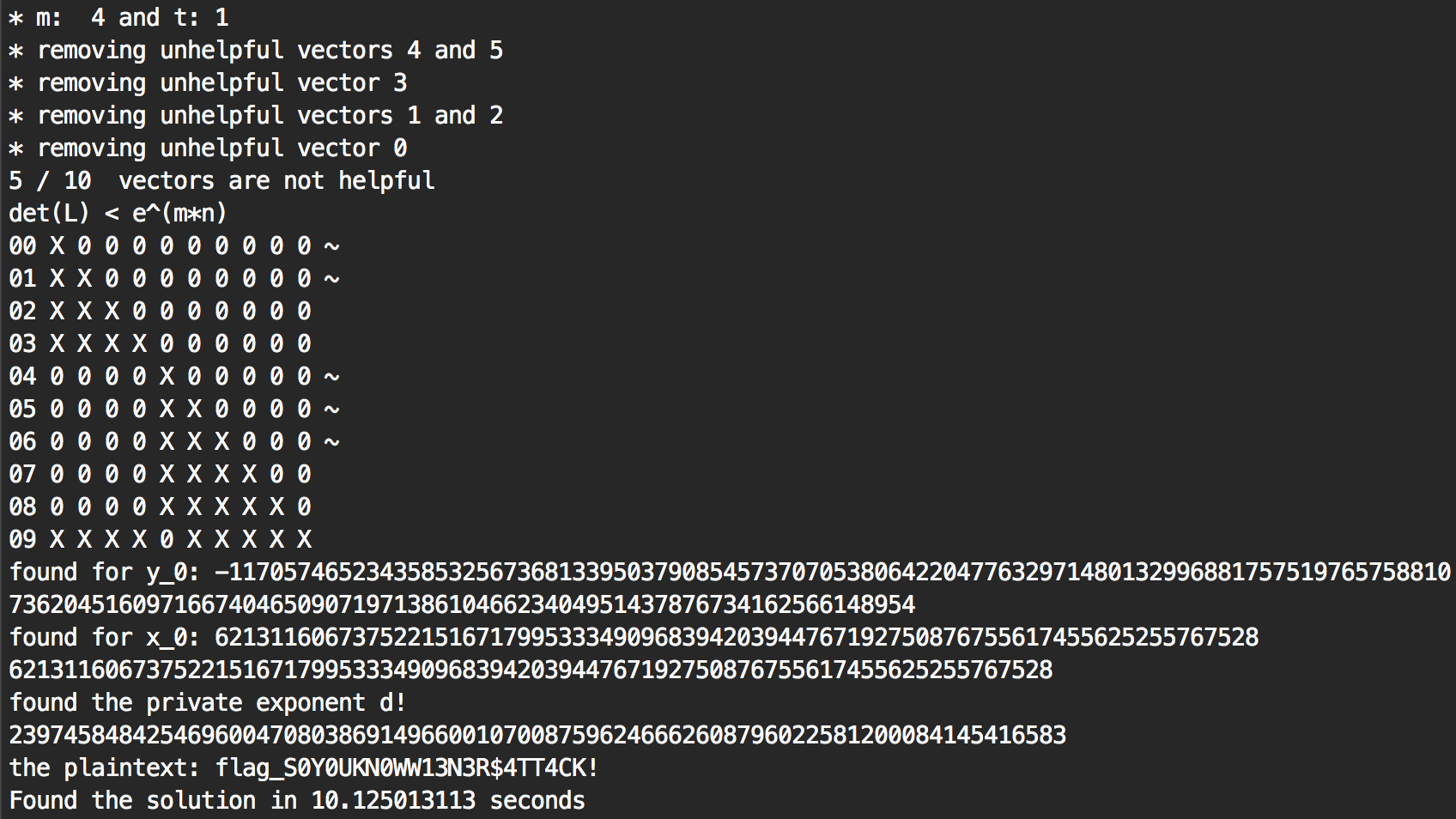
That’s right, only 10 seconds. Because I removed some unhelpful vectors, I could use the value m=4 and it worked. The original algorithm needed m=5 and needed a lattice of dimension 27 when I successfully found a lattice of dimension 10 that worked out. I guess the same thing happened to the 59 triplets before that and that’s why the program ran way faster. 3 minutes to 10 seconds, I think we can call that a success!

The original code: