A journey into zero-knowledge proofs posted October 2023

My journey into zero-knowledge proofs (ZKPs) began in university, with me slouching in an amphitheater chair attending a cryptography course. "Zero-knowledge proofs", said the professor, "allow a prover to convince a verifier that they know something without revealing the something". Intriguing, I thought. At the end of the course I had learned that you could prove simple statements, like the knowledge of the discrete logarithm of a field element (e.g. that you know $x$ in $y = g^x \mod p$ for some $g$ and prime $p$) or of an isomorphism between two graphs. Things like that.

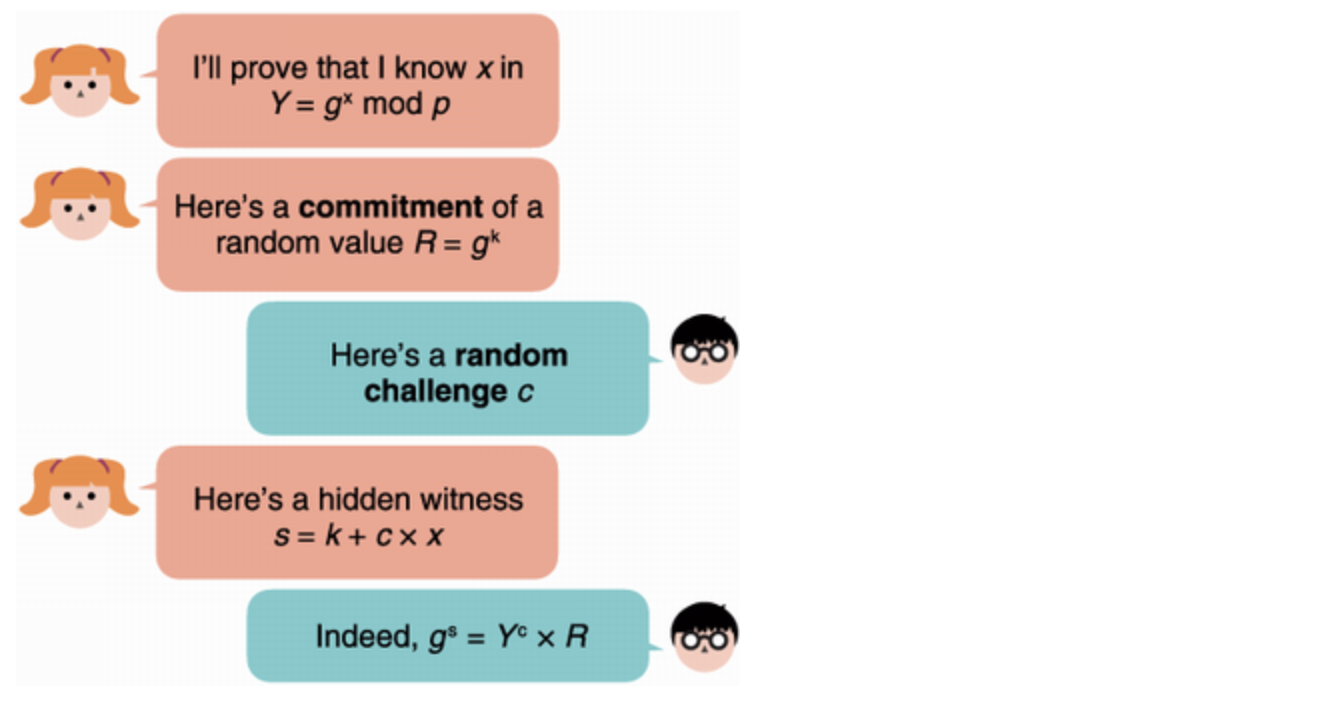
The protocols we learned about were often referred to as "sigma protocols" due to the Σ-like shape the interaction between the prover and the verifier looked like. The statements proven were quite limited and simple and I remember thinking "this is interesting but where is this used?"

It took me some time to realize that the cryptographic signature schemes used all over the place were actually zero-knowledge proofs. Non-interactive zero-knowledge proofs specifically. As in, no back-and-forth had to happen between a prover and a verifier. The prover could instead create the proof by themselves, publish it, and then anyone could act as a verifier and verify it. I wrote about this first discovery of mine in 2014 here.

Anyone familiar with these ZK proofs would tell you that the non-interactivity is usually achieved using a transformation called "Fiat-Shamir", where the messages of the verifier are replaced by hashing any messages sent previously. If the hash function acts random enough, it seems to work. Although, this technique can only be applied when the verifier messages are not structured, and are just random values. Sigma protocols that have verifiers who only send random values as part of the protocol are referred to as "public-coin".

In 2015 I moved to Chicago and joined NCC Group as the first intern in a new team called Crypto Services. It was a small team of cryptographers led by the fantastic Tom Ritter, and we mostly focused on auditing cryptographic applications. From TLS/SSL to secure messaging, we did it all. These were transformative years for me, as I got a crash course in applied cryptography, and got to work with truly amazing people (like the Thomas Pornin!)

At some point cryptocurrencies started booming and we switched to auditing cryptocurrencies almost exclusively. The second time I encountered zero-knowledge proofs was during an audit of ZCash, a fork of Bitcoin that used ZKPs to hide who sent how much to who. This was mind-blowing to me, as the statements proven were not "simple" anymore. What was proven was actual program logic.

This new kind of "general-purpose" zero-knowledge proofs seemed like a game changer to me. It took me some time to understand the interface behind these ZKPs, but let me try to give you the gist using sudokus. I believe that if you understand this simple example, you can then understand any type of application that makes use of ZKPs by abstracting the zero-knowledge proofs as black boxes.

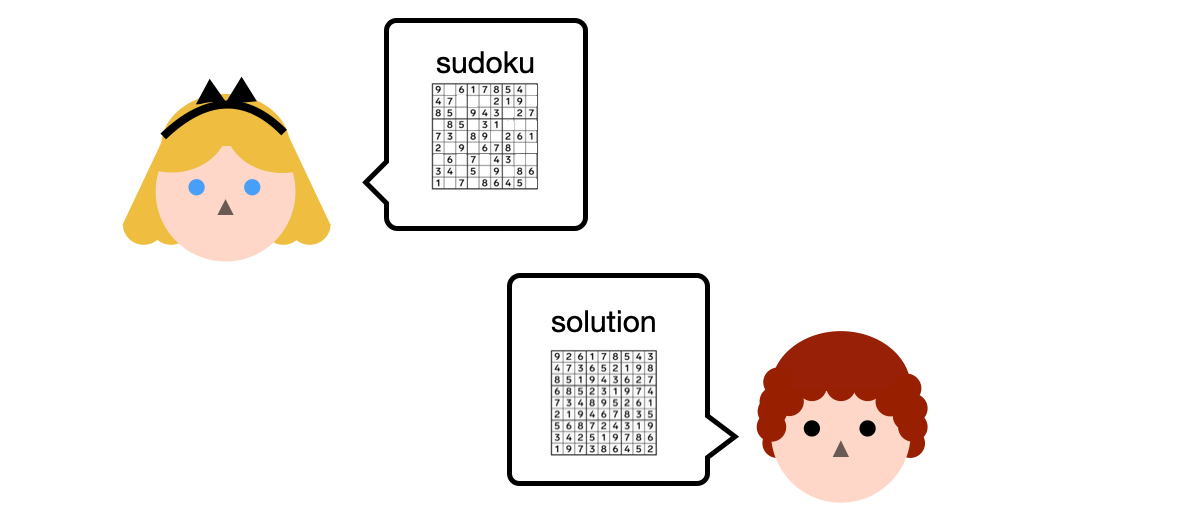
In this scenario, Alice has a sudoku grid and Bob has a solution. Also, they both have access to some Python program on Github that they can use to verify that the solution solves Alice's grid.

Bob could send the solution to Alice, and she could then run that program, but Bob does not want to share his solution. So Bob runs the program himself and tells Alice "I ran it with your grid and my solution as inputs, and it output true". Is this enough to convince Alice?

Of course not! Why would Alice trust that Bob actually ran the software? For all she knows he could have done nothing, and just lied to her. This is what general-purpose zero-knowledge proofs solve: they allow Bob to create a proof of correct execution given some public inputs (Alice's grid) and some private inputs (Bob's solution).

More specifically, both of them can take the "verify solution" program and compile it to two asymmetric parts: a prover index and a verifier index (also called prover key and verifier key, although they're not really keys). Bob can then use a proving algorithm with the correct arguments to produce a proof, and Alice can use another algorithm (a verifier algorithm) to verify that proof. To do that she of course needs to use the verifier index (which is basically a short description of the program) as well as pass the sudoku grid as public input (otherwise who knows what sudoku grid Bob used to create the execution proof).

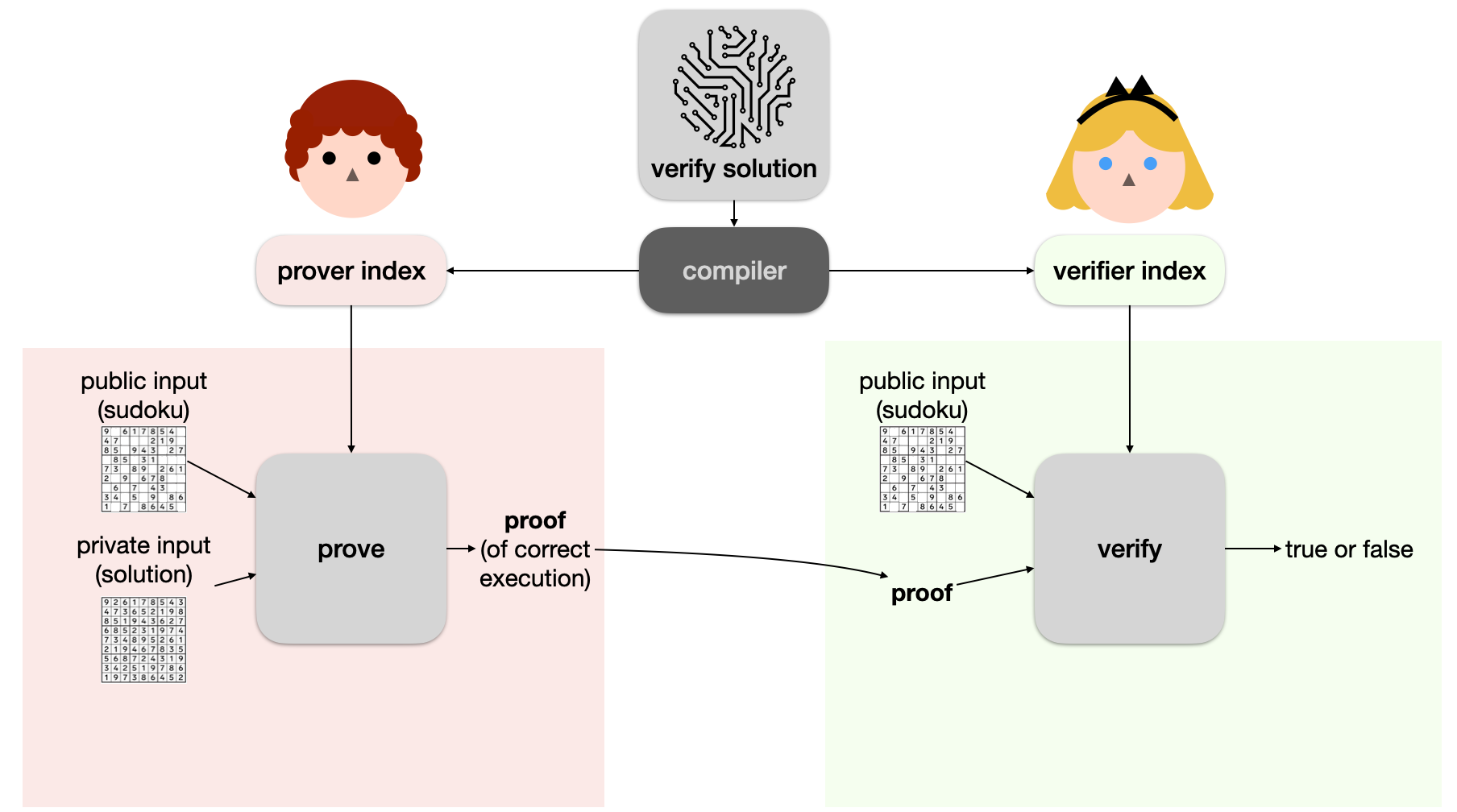
Python programs are of course not really something that we can prove using math, and so you'll have to believe me when I say that we can translate all sorts of logic using just the multiplication and addition gates. Using just these, we form arithmetic circuits.

I'll give you some examples that come up all the time in circuits people write:

• here's how you constraint some value to be a bit: $x ( x - 1 ) = 0$
• here's how you unpack a value into bits: $x = x_0 + x_1 \cdot 2 + x_2 \cdot 4 + \cdots$
• here's how you do an XOR between two bits (this one is cute): $a + b - 2ab = 0$
• here's how you do an if else condition to encode something like r = if cond { a } else { b }: $r = \text{cond} \cdot a + (\text{cond} - 1) b$.

And so, you can imagine that what people end up proving are lists of such equations where the variables are "wired" between different equations (for example, an XOR would use variables that are also constrained to be bits).

To prove that a list of equations is correct given some values, you would then record all of the values used to fill the equations during execution (an execution trace if you will) and apply some math magic on it.

That's all I'll say about that but you can check my series of videos on plonk (a proof system) to learn more about that part.

But let's go back to the project I was looking at at the time. Zcash used a proof system called Groth16. Groth16 was, as the name indicates, created in 2016 by a Mr. Groth. 2016, in the world of zero-knowledge proofs, sounds like centuries ago. Things go really fast and new schemes and breakthroughs are published every year. Yet, one can say that Groth16 is still competitive today as it remains the proving scheme with some of the smallest proofs (hundreds of bytes). In addition it is still used all over the place. Most ZK apps that I've seen being built, or that have been built, on top of Ethereum are using Groth16.

The reason might be that some of the tooling available has dominated the space: Circom and snarkjs. Circom allows you to write circuits in a format Groth16 can understand, and snarkjs allows you to prove and verify these on your laptop, as well as verify proofs on Ethereum (via a verifier implemented in Solidity).

In the following screenshot you can see what Circom code looks like on the left, and how the code is converted down to equations (called constraints) on the right. This is obtained via circomscribe. Take some time to understand what the code does, and how the compiled constraints end up enforcing the same logic.

You might have noticed that none of the equations/constraints have a higher degree than 2. This is a limitation of the arithmetization that Groth16 supports, which is called R1CS. The term arithmetization here is used as to refer to the format that your constraints or equations have to be in for them to be provable by the proof system. This is important as not all proof systems enforce the same "encoding" for your circuit, some allow more complex equations to be packed, while others force you to break down your equations into smaller ones (which increases the list of equations, and thus is more expensive).

Briefly, the way R1CS works is that each equation/constraint has the ability to perform the multiplication of two linear combinations of any of your witness values (the values in the execution trace) and enforce that the result is equal to another linear combination. If that doesn't make sense think of it this way, what you do in R1CS is to encode your circuits as a number of variables $a_i$, $b_i$, and $c_i$ such that if your execution trace is the vector of values $\vec{w} = (w_0, w_1, \cdots)$ then each of your constraints will look like this:

$$ (a_0 w_0 + a_1 w_1 + \cdots)(b_0 w_0 + b_1 w_1 + \cdots) = c_0 w_0 + c_1 w_1 + \cdots $$

Imagine that we wanted to constrain that $w_1$ is a bit (it's equal to 0 or 1), then we'd try to hardcode a new set of values $a_i, b_i, c_i$ such that we get $w_1 (w_1 - 1) = 0$.

We could set $a_i = b_i = c_i = 0$ except for: $a_1 = 1$ and $b_1 = 1$ which would get us to $(1 \cdot w_1)(1 \cdot w_1) = 0$ which is close but not exactly what we want. How do we get the $-1$ in there?

The solution to encode constants in your circuit is to require that one of the witness values is fixed to a known value. This is done via the proof system (and not by R1CS itself), and usually we set $w_0 = 1$. This way by setting $b_0 = -1$ we get what we want. Right?

Note: additionally, we usually enforce the following witness values $w_1, w_2, \cdots$ to contain the public input values, and then everything after that are private variables that will be used to store the prover's execution trace.

Now, let me say one last thing about Groth16 before moving on. The scheme sort of sucks massively in other ways, because it requires a trusted setup. I've explained what trusted setups are here, but I'll briefly repeat it here: Alice, Bob, or whoever wants to use Groth16 has to generate a set of parameters first. This generation of parameters is unfortunately dangerous, as the person who performs it will be in possession of some values that will let them forge proofs. So-called toxic waste.

We're not crazy, so the way we deal with this is to have someone we trust run the generation of parameters and then destroy the toxic waste they produced during that. This explains the "trusted" part in "trusted setup". Relying on the goodness of a single person is usually not enough to convince people, and so the trusted setup is normally ran by many people in a multi-party computation kind of protocol (called a ceremony). This ensures that as long as one person is honest, the whole thing is secure.

This doesn't always work out. In 2018, Ariel, an employee of Zcash, found a bad bug. Turns out Zcash's ceremony had been run incorrectly and people could have minted money out of thin air. The fix (and a subsequent new ceremony) took a year to land.

What doubly sucks with Groth16 is that you need such a ceremony per-circuit. Every change you want to make to your circuit, or every new circuit you want to prove, will require you to go through that painful ceremony thing again. On top of that, I would say that the tooling to do such ceremonies is in quite an experimental shape.

In 2018, while still working at NCC Group, Ava brought me to the announcement party of the Coda protocol blockchain. There I learned that this project used zero-knowledge proofs in a novel way: they recursed them! Using proofs to prove other proofs, ad-infinitum.

After the meetup I went on their webpage that at the time hosted a demo that looked like that:

Zero-knowledge proofs managed to blew my mind once more. Unfortunately the demo doesn't exist anymore, but if you could experience it today you would have see that: a webpage taking seconds to synchronize to a testnet's latest state (with some cool animations) and then proceeding to verify each new block being added on top of the latest one, live.

At the time this was something I had never seen. Bitcoin or Ethereum were cryptocurrencies that got longer and longer with time. And if you wanted to synchronize your client to their network, you'd have to wait for it to verify the chain block by block, which could take days or even weeks (and perhaps months today). Coda's demo would do that in mere seconds.

ZKPs gave the whole "trust but verify" a whole new meaning.

Each new block would carry a proof, which would prove the correct validation of the entire block and its transactions, and the correct application of the transactions to the previous state resulting in the latest state. On top of that the proof contained a proof that the previous proof was correct. And the previous proof contained a proof that the previous block was correct, along with the previous previous proof. And on and on. You get the idea.

Back then I couldn't believe what I had seen. It seemed too magical, too good to be true. Later I learned how recursive proofs worked and some of the magic dissipated. Intuitively, you can think of it like this: if these zero-knowledge proofs allow you to prove any sort of programs, then why not prove a verifier? The proof verifier is just some software, like any other software, and so its execution can be proved as well!

This novel idea brought some new use cases with it: you could now prove long-running computations. Year-long computations if you wanted. It also brought some novel problems with it that are worth mentioning: recursion is expensive. The reason is that in general, while verifying is cheap (in the order of milliseconds), proving is expensive (in the order of seconds). And so, if recursing meant creating a proof at each step, it meant paying some heavy cost at each step.

In 2019, Sean from Zcash ended up coming up with some techniques called Halo to defer some of that cost to the very end. More recently, a new technique called folding was independently proposed by Srinath (via his scheme Nova) and Benedikt and Binyi (via their scheme Protostar) which allows recursion to completely bypass the expensive computation of a proof at every step. Folding allows us to directly recurse on the execution trace. I call it pre-proof recursion. Of course, folding comes with its different set of challenges and limitations but this is for another article.

In 2018 I decided to move from the service industry to work on a product: Libra (later renamed Diem). I served as the security lead there for two years, in which I ended up writing a book: Real-World Cryptography. This was the culmination of two years of work, and you can read more about why I decided to write yet another cryptography book here. The book contains a chapter on zero-knowledge proofs (and MPC and FHE), as well as a chapter on cryptocurrencies which I believe makes it the first (and perhaps still the only) book with a chapter on cryptocurrencies. Believe it or not.

If you're enjoying my writing thus far, and you don't have a copy yet, you should buy the book and leave me a good review on Amazon. Obviously!

Not much happened ZK-wise in my life during my time at Facebook. The only thing I can remember was learning about Celo's Plumo protocol and pushing for similar ideas internally. The idea behind Plumo was similar to Coda protocol, but instead of using recursive zero-knowledge proofs to prove the whole blockchain, it relied on the consensus protocol of the Celo blockchain to do most of the work. Left to the zero-knowledge proof was to verify a number of signatures. Sometimes a number of signatures so large that Plumo used a very big proof as well as beefy computers in the cloud to compute it.

it is possible create proofs that span half a year worth of epochs for 100 validators in about 2 hours. We evaluated the performance of our verifier on a Motorola Moto G (2nd Gen), a 2014 mobile phone with 1GB RAM and a Quad-core 1.2 GHz Cortex-A7 processor. We used an unoptimized implementation, directly cross-compiled from [GS19]. The results show it is possible to verify such a proof in about 6 seconds.

I'm not sure why the proof takes so long to verify, but the proving time says a lot about the performance of zero-knowledge proofs in 2020. Since then, a LOT has happened (including folding) and it is probable that the proving time is much more reasonable now.

Unlike AI, which has opened the way to so many applications, it is always hard for me to think of interesting applications for zero-knowledge proofs. My current mental model is the following: the privacy features of ZKPs (provided by the "ZK") seem to mostly be useful when they impact end-users directly. Privacy has been very useful in cryptocurrencies, where everything is public by design, and the word public mixed with money leads to obvious issues. But outside of cryptocurrencies, I have a hard time seeing a large adoption of ZK thanks to its privacy features.

People don't care about privacy. Users want something that's fast and that has a good user experience. If they have to choose between two applications where one is a better experience, but the other provides privacy, they will choose the one with a better experience over the privacy-enhanced one. I've seen this happen again and again (encrypted emails, encrypted messages, cryptographic algorithms, etc.)

People also generally don't care about the "verifiable computation" aspect. Every day we agree to trust many establishments and other human beings. This is how society works, and nothing would work without this kind of network of trust. As such, the high-degree of assurance that ZKPs provide are often unnecessary, and if more trust is needed signatures are often enough.

Between machines though? When no users are involved, the compression and verifiable computation aspects of zero-knowledge proofs are totally a game changer, and I believe that these are going to be the two aspects of ZKPs that are going to impact the non-blockchain world.

I said that signing is often enough, and ZKPs are overkill in a number of scenarios, but verifying signatures in a ZKP is something that actually leads to interesting and useful applications. Both Coda protocol and Plumo did exactly this (verifying consensus and transaction signatures for nodes/light clients). More recently, Sui came out with zkLogin which allows you to prove that a platform (e.g. Google) signed over your username/mail without leaking that information, and Aayush and Sampriti came up with zkEmail which allows you to verify that your email provider signed on the fact that you received some email without leaking the content or your email.

At some point in 2021, the writing was on the wall that Libra was not going to launch. I was still thinking about ZK a lot, and also about the lack of progress I had made in this field. I decided to join the project that had blown my mind a few years prior: Coda Protocol. Their name was now Mina protocol (apparently they had been sued into changing name). I ended up joining and working there for two years on their proof system as a cryptography architect.

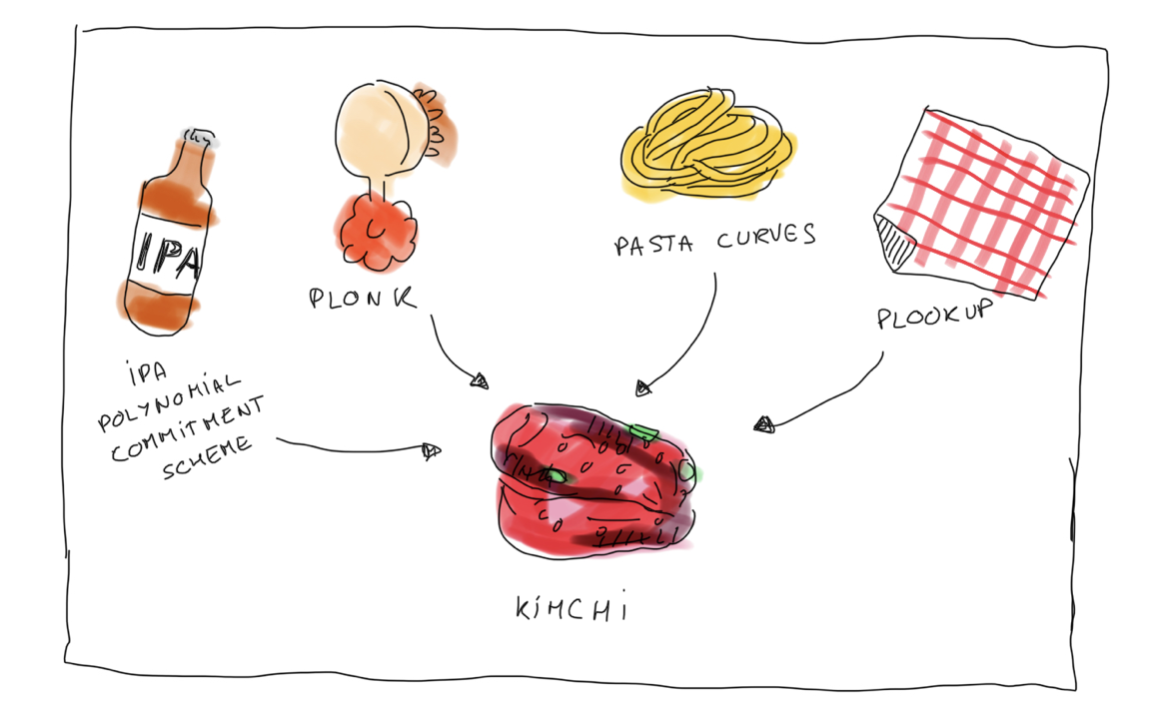
The proof system was called Kimchi, which was a variant of PlonK. PlonK had been released in 2019, and had been a game changer in the field, introducing an efficient universal scheme which got rid of Groth16's ugly per-circuit trusted setup. Now a single trusted setup was enough to last for a lifetime of circuits (as long as the circuits didn't reach some upper bound size).

PlonK also brought a different arithmetization, moving us from R1CS to something more flexible (that people often refer to as the "plonkish arithmetization"). No more quadratic constraints, now you could come up with higher degree equations for your constraints as long as they were limited to act on a small part of the execution trace (if that doesn't make sense don't worry). The R1CS tooling was lost though, and PlonK implementations were often incompatible with one another.

Around the same time, Marlin, a universal scheme for R1CS was also released. PlonK won the popular contest though, and a long line of papers started forming around the construction: turboplonk, plookup & ultraplonk, fflonk, shlonk, hyperplonk, honk, etc.

I wouldn't do the space justice without mentioning transparent schemes. Transparent schemes are proof systems that completely bypass the trusted setup: you can generate the parameters to use them without having to do a ceremony! (In other words, Alice, Bob, and anyone can generate them by themselves.)

So-called STARKs (where the T is for transparent) formed a bubble at the same time as the Plonk and Groth16 bubble. These schemes had much faster provers at the cost of larger proofs. If Groth16 had proofs of hundreds of bytes, STARKs looked like hundreds of kilobytes. In addition, due to their use of hash functions they boasted resistance against hypothetical quantum-computers. More seriously they have been criticized for using lower security parameters compared to other schemes.

Another notable line of work of transparent ZKP based on the discrete logarithm problem are inner product arguments (IPAs). Most people know the bulletproof scheme for its use in the Monero cryptocurrency. Unlike other schemes, IPAs have slower verifiers (although still in the order of ms), which can be an issue in practice, but unlike STARKs can still claim to have small proofs.

Interestingly, people have mixed PlonK with the two previously discussed schemes. Plonky mixes PlonK with STARKs, and Zcash's Halo 2 mixes PlonK with IPAs (which is what we used at Mina).

During my time at Mina, most of the company was focused on shipping zero-knowledge smart contracts (or zkapps). The idea was pretty simple: smart contracts in Ethereum (and similar cryptocurrencies) were inefficient in parts due to everyone having to re-execute transactions over and over.

This was the perfect problem to solve for zero-knowledge proofs as one could just execute a smart contract once and then provide an execution proof for others to verify. Avoiding the cost of recomputing the same thing over and over.

One issue when smart contracts are executed locally, on people's laptops, is that they might prove conflicting state transitions. Imagine that someone's transaction takes a smart contract from state A to state B, and someone else's transaction takes the same smart contract from state A to state C, then whoever's transaction gets in first will invalidate the other one. The two transactions are racing.

The problem is that each execution proof has the precondition that the state must be A for it to be valid. In practice this means that the network verifies the proof using the state as public input, and so if the state is no longer "A" then the proof won't verify.

Preconditions can be more relaxed than "this public input MUST be equal to this specific value for the proof to be valid". You can, for example, enforce that the a public input has to be higher than some value, or something like that. But this relaxation also limits the number of applications one can build.

To solve this problem of resource contention, Mina separates the logic of smart contracts into two parts: a private part that doesn't lead to conflicts (and is thus highly parallelizable), and an optional final intent. Final intents are ordered by the network (consensus specifically) and queued up for some time. Other parts of the smart contract can then be used to process that queue. That "post-ordering" execution is lagging behind, and who performs it is a choice of the application.

Aleo, another cryptocurrency similar to Mina, has a similar approach except that their final intent is an actual logic that is executed by the network. The network does that right after processing the transaction (and verifying its ZKP). While both solutions have the network order transactions, Aleo decides to provide a smoother developer experience (at a cost for the network) by taking the burden of executing the final intent in the same fashion Ethereum does.

Note: another worthy contender is Starknet, who decides to bypass this issue by not allowing users to create the proofs at all, and by letting the network sequentially create proofs after some ordering/sequencing of the transactions. The whole purpose of Starknet is to create proofs of execution that Ethereum can verify (making Starknet a "zkrollup", the best kind of "layer 2").

Another issue to solve, if one wants to emulate Ethereum-style smart contracts, is to support contracts calling other contracts. Both projects do this by having each nested call be its own proof, and by having the verifier (the network) glue the calls (but really the proofs) together.

More specifically, one can imagine that at the moment of calling another smart contract's function, a circuit can simply advertise (we also say "witness publicly") what arguments it is using to call the function with, and then advertise the resulting value of the call. It is up to the verifier to verify that the call was correctly encoded by plugging the input and output values as public inputs in the verification of both the caller and callee circuits.

There's something I've sort of shied away from talking about so far: writing circuits. If proof systems can be thought of as backends, then circuit writing is the frontend.

Mina's solution is to provide a library in Typescript (called o1js). That's the "embedded-DSL (Domain Specific Language)" approach. With such a library people can keep using their favorite language, at the cost of writing code that might not produce constraints (and thus produce vulnerabilities). Here's what a Mina zkapp looks like written with o1js:

Several projects have followed this approach. For example, there's arkworks-r1cs for writing R1CS circuits in Rust, and there's gnark for writing circuits in Golang.

Another approach is to invent a new programming language. That's the approach taken by Circom which I've mentioned before. More recently Noir (by Aztec Network) and Leo (by Aleo) were introduced as Rust-like languages. Interestingly Aleo also has a VM that can be compiled into a circuit (so a more low-level-looking language in some way).

Finally, there's the approach of letting developers use their favorite language without having to write code in a specific "circuit way". By that I mean that we can compile the Rust/Golang/C/etc. code they write into a circuit directly. This is the approach of zkLLVM which supports any language that uses the LLVM toolchain/compiler, and translates the LLVM intermediate representation (IR) directly into a circuit.

But wait, I lied, I'm actually not done. There's another completely different proposition: zkVMs. If the previous approach was about "encoding your logic into a circuit", the zkVM approach is about "encoding a Virtual Machine into a circuit".

A VM is essentially just a loop, that at every iteration loads the next instruction and executes it. This is logic in itself that can be converted in a circuit, which would load another program and run it to its course. This is the idea behind the concept of zkVM. It is a very attractive idea because it removes a number of bugs that only happen when you're writing circuits directly (as long as the VM circuit itself doesn't have bugs of course). It also makes loops, branching, etc. much more efficient.

In zkVM-land, there's two branches of philosophy: targeting existing VMs and inventing your own VM.

For example, Risc0 and Jolt both target the RiscV VM. There's also been some ZKWASM projects (like this one). In crypto-land, there are dozens of zkEVMs which all attempt to target the Ethereum VM.

Why would anyone invent new VMs? The idea is that the other VMs I've mentioned are not optimized for being encoded as circuits. And so there's been a line of work to invent optimal zkVMs. For example, there was Cairo (which has an amazing whitepaper) and Miden (which has amazing doc), and more recently Valida (productionized by Lita).

I recently quit my job to launch zkSecurity with two of my ex-coworkers Gregor and Brandon. The idea being that zero-knowledge proofs are going to change the world, and I'll be the first to move into the security for ZK space (hence the great choice of name).

We've been booked non-stop, and have released some interesting blogposts, interesting tools, as well as some interesting public reports. Check it out!

We're also helping organize Zprize, the largest competition in ZK. The idea of ZPrize is to accelerate what is today a technology that's practical for applications that remain relatively simple, but that could be practical for a much larger number of applications if the technology were to gain some efficiency boost.

ZKPs are not FHEs (in that they're practical today), but they still have a number of speed issues to overcome. Mostly, not all operations are practical to encode in circuits. Circuits are encoded over a field (think numbers modulo a large prime number), and don't play nice with anything that requires a lot of bitwise operations (impacting basically all of symmetric cryptography) or bigint arithmetic (impacting basically all of asymmetric cryptography). This means that in general, simple things like doing XORs and checking if values are within a certain range easily blow up the size of our circuits. This leads to provers being slow and using a lot of memory.

There's been three ways to tackle these issues:

1. screw it, we'll run things on beefy machines in the cloud
2. let's figure out how to accelerate these operations in order to reduce the circuit size
3. screw it, let's break up a circuit into multiple smaller circuits

The first solution works somewhat well for machine-to-machine applications that provide mostly compression of computation. For privacy applications targeting end-users? It's often more tricky as users don't want to share their private inputs to some untrusted machine in the cloud. For this, there's been some interesting lines of work that decentralize the prover using multi-party computation protocols, so that delegating a proof doesn't mean losing privacy. The latest work that I know of is zkSAAS from Sanjam.

Still, finding better proof systems and accelerating awkward operations has been one of the most successful ways to solve the efficiency problem. The major breakthrough was to use lookups. For example, integrating an XOR table to your proof system so that you can quickly get the XOR of 4-bit variables, or integrating a table with all the numbers from 0 to $2^{12}$ to allow you to quickly check if a number is within a certain range. Ariel was the first one to introduce a lookup scheme (called plookup) in 2020, which was followed by a stream of improvements, up to the more recent Lasso which basically claims that lookups are so efficient that we can now implement a zkVM using lookups only (isn't that crazy?)

Finally, breaking a circuit into smaller circuits is something I've already almost mentioned (but you might have missed that): using recursion and/or folding one can break a circuit into smaller circuits! Nova Scotia does exactly that by upgrading Circom to use the Nova folding scheme.

There's so much more I could say, but I've now reached 5,000 words and it's getting late. I hope you appreciated the wall of text, and if you have your own ZK journey I encourage you to write about it as well :)