Juniper's backdoor posted December 2015

A few days ago, Juniper made an announcement on 2 backdoors in their ScreenOS application.

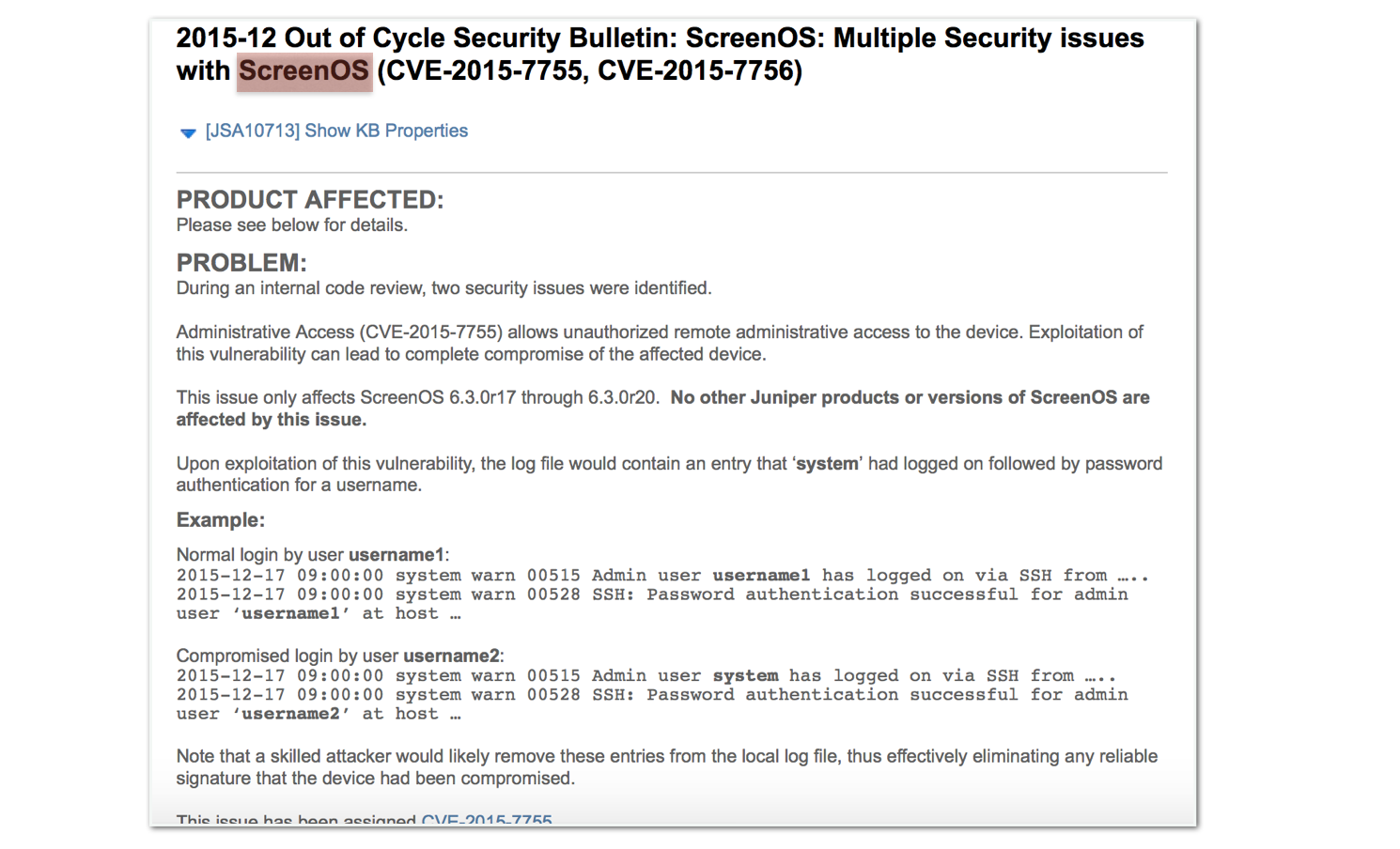
But no details were to be found in this advisory. Researchers from the twitter-sphere started digging, and finally the two flaws were found. The first vulnerability is rather crypto-y and this is what I will explain here.

First, some people realized by diffing strings of the patched and vulnerable binaries that some numbers were changed

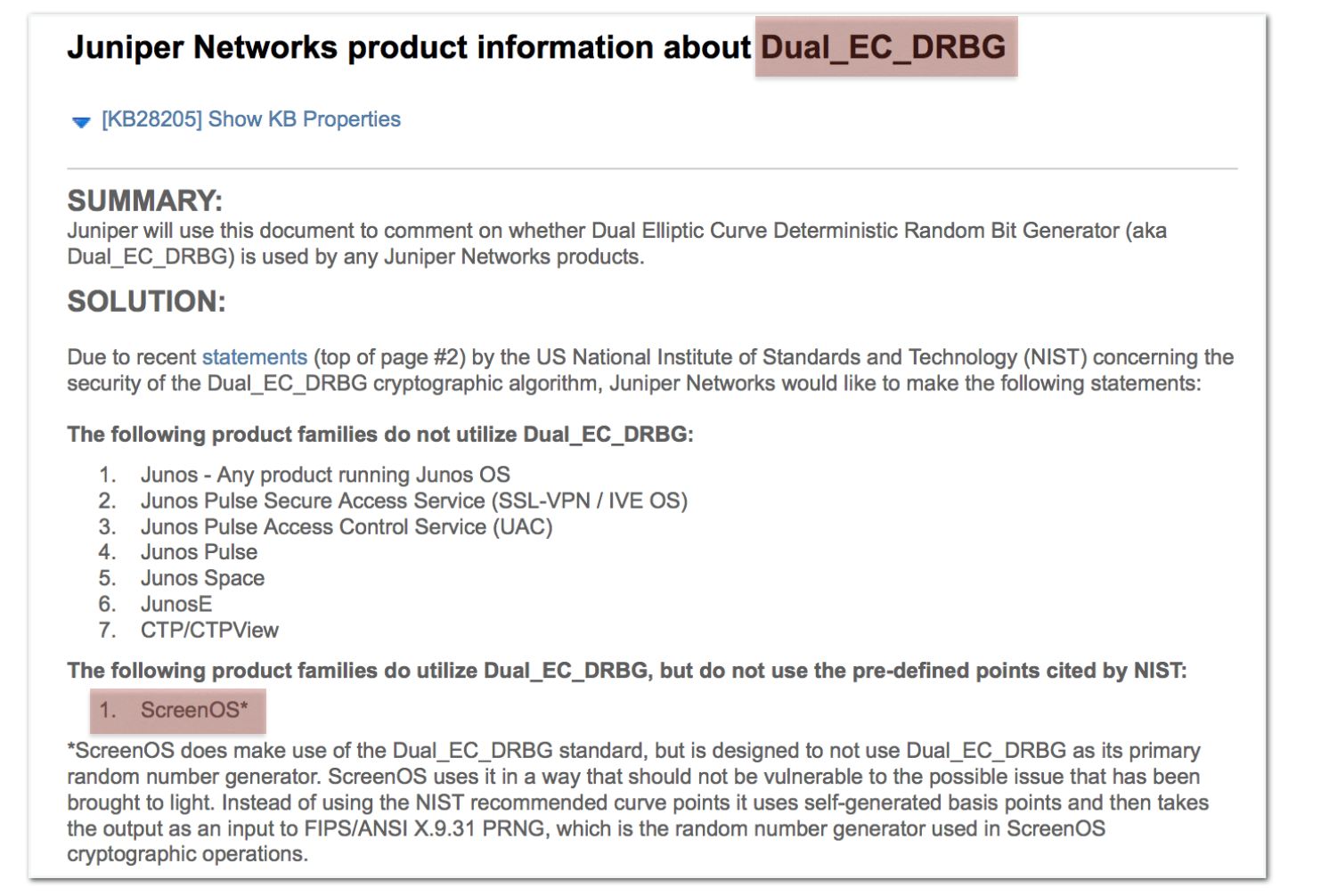
Then they realized that these numbers were next to the parameters of the P-256 NIST ECC curve. Worse, they realized that the modified values were these of the Dual EC PRNG: from a Juniper's product information page you could read that Dual EC had been removed from most of their products except ScreenOS. Why's that? No one knows, but they assured that the implementation was not visible from the outside, and thus the NSA's backdoor would be unusable.

Actually, reading the values in their clean binaries, it looks like they had changed the NSA's values introducing their own \(Q\) point and thus canceling NSA's backdoor. But at the same time, maybe, introducing their own backdoor. Below the NSA's values for the point \(P\) and \(Q\) from the cached NIST publications:

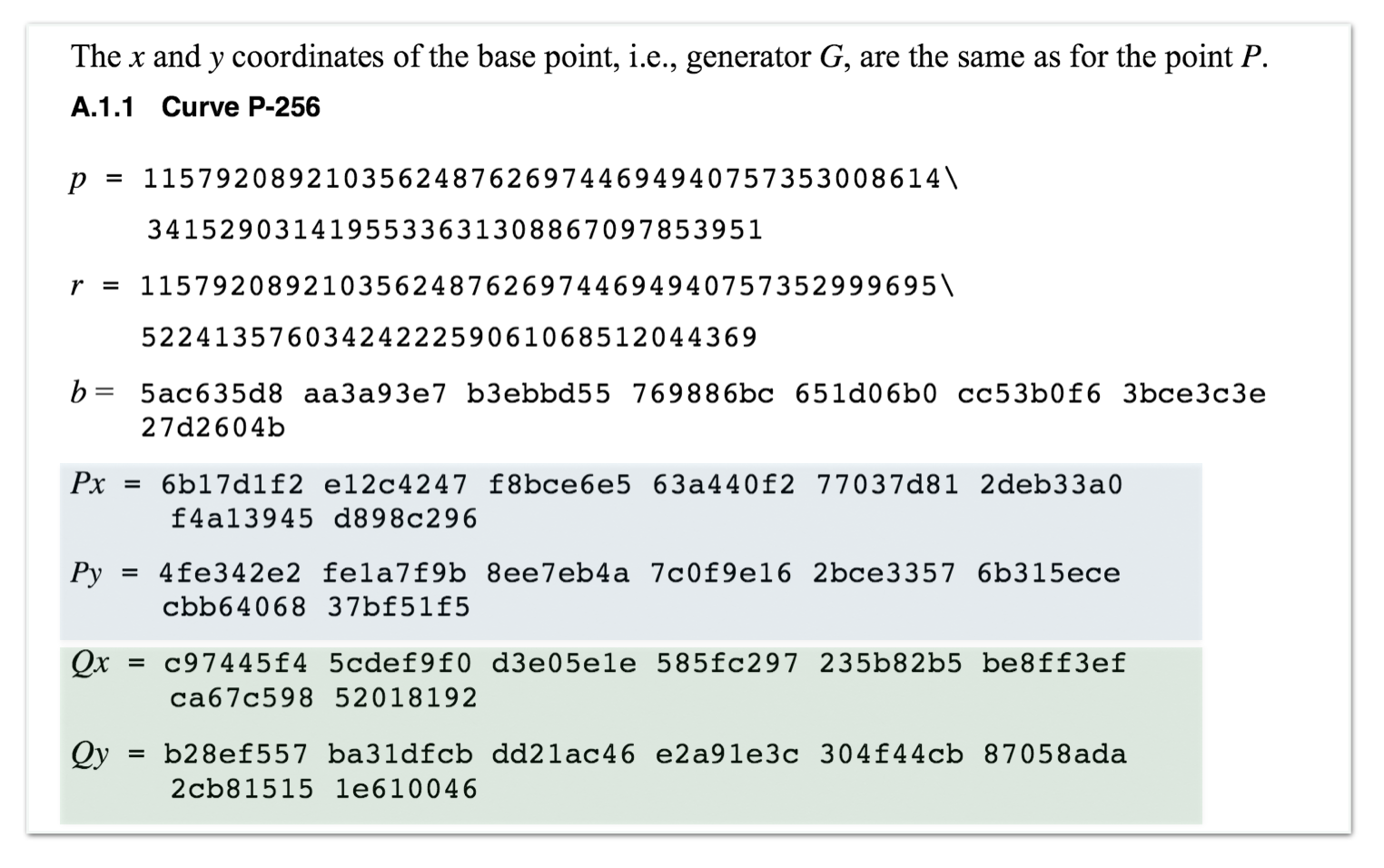
Reading the previous blog post, you can see how they could have easily modified \(Q\) to introduce their own backdoor. This doesn't mean that it is what they did. But at the time of the implementation, it was not really known that Dual EC was a backdoor, and thus there was no real reason to change these values.

According to them, and the code, a second PRNG was used and Dual EC's only purpose was to help seeding it. Thus no real Dual EC output would see the surface of the program. The second PRNG was a FIPS approved one based on 3DES and is -- as far as I know -- deemed secure.

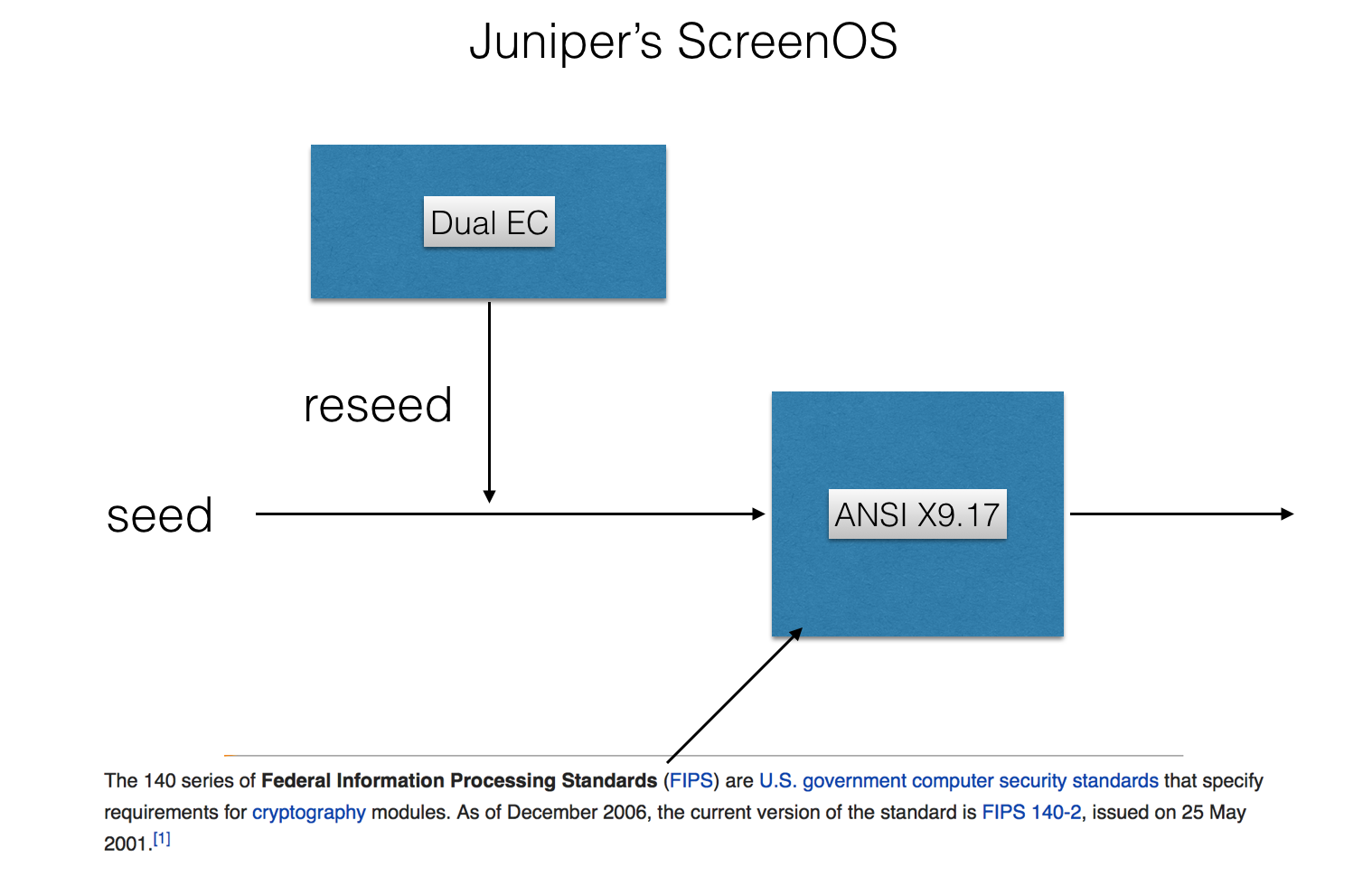
Another development came along and some others noticed that the call for the second PRNG was never made, this was because a global variable pnrg_output_index was always set to 32 through the prng_reseed() function.

Excerpt of the full code:

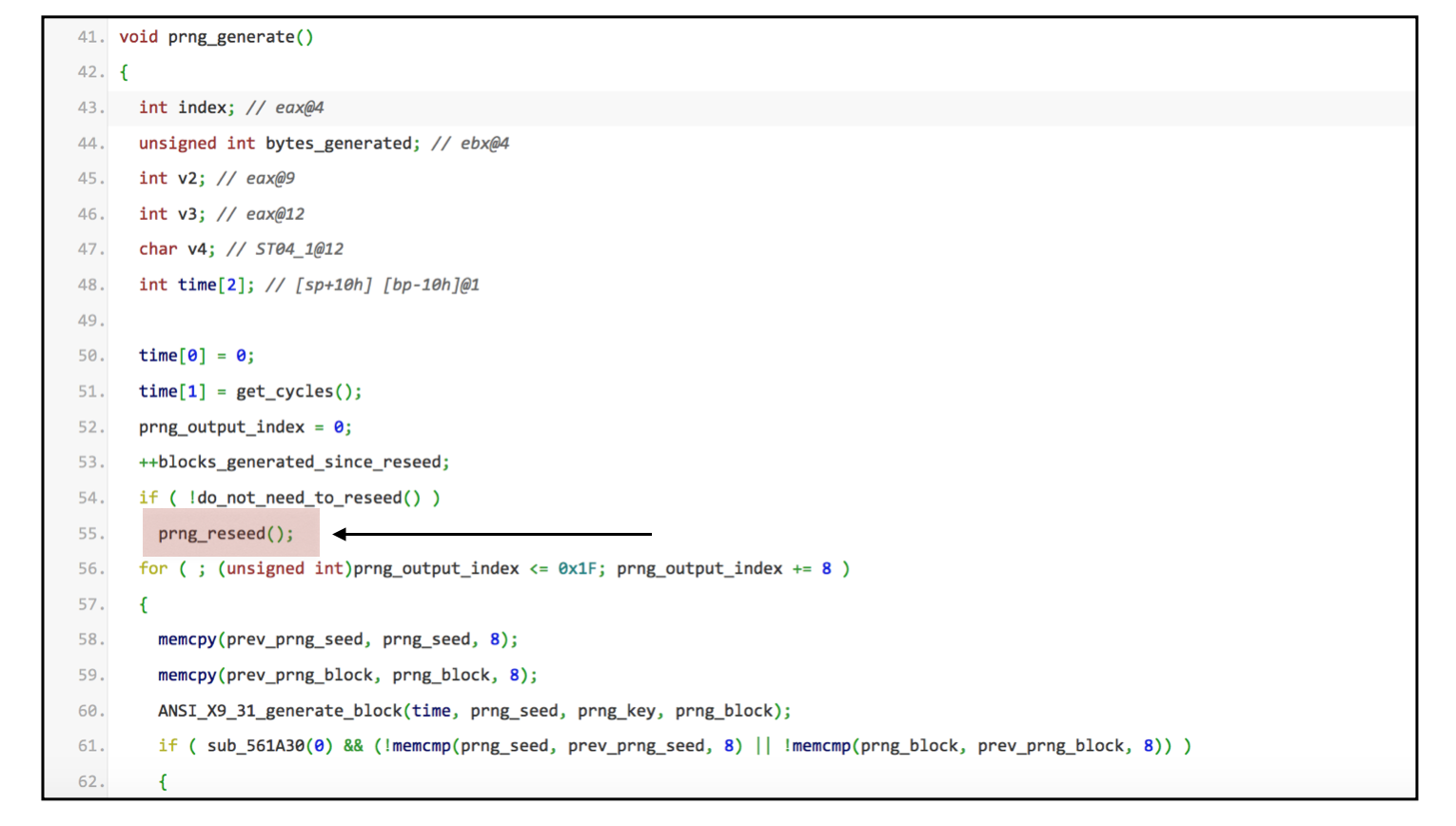
This advance was made because of Juniper's initial announcement that there were indeed two vulnerabilities. It seems like they were aware of the fact that Dual EC was the only PRNG being used in their code.

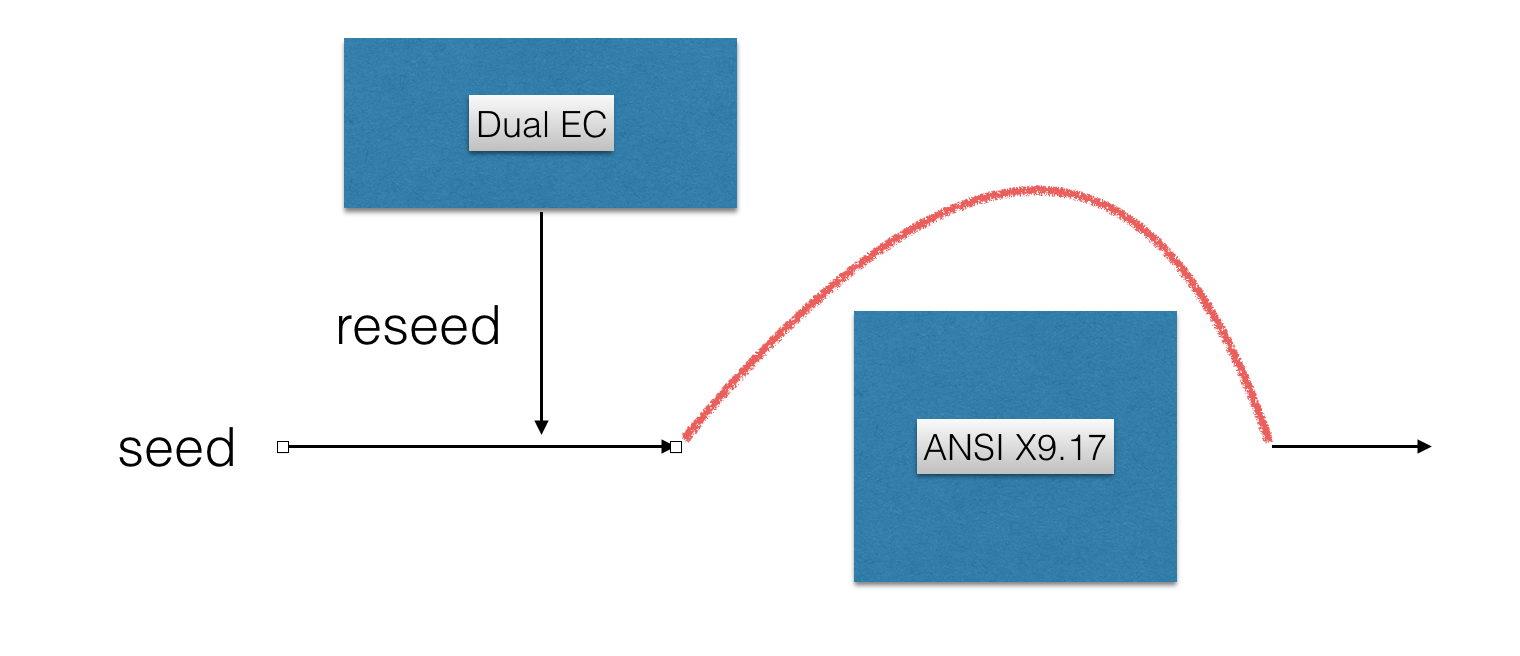
Now, how is the Dual EC backdoor controlled by the hackers? You could stop reading this post right now and just watch the video I made about Dual EC, but here are some more explanations anyway:

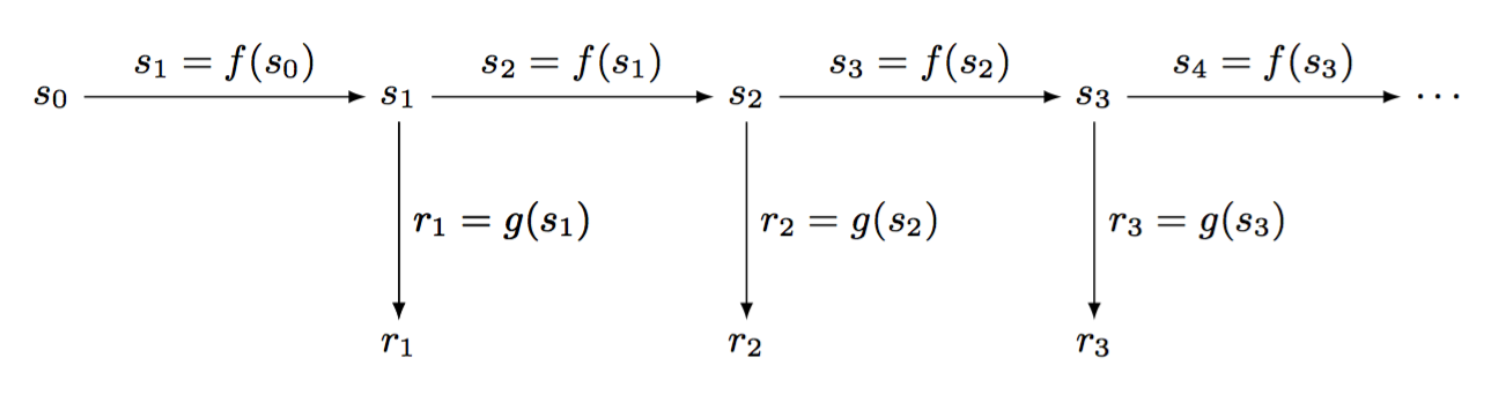
This above is the basis of a PRNG. You start it with a seed \(s_0\) and every time you need a random number you first create a new state from the current one (here with the function \(f\)), then you output a transformation of the state (here with the function \(g\)).

If the function \(g\) is one-way, the output doesn't allow you to retrieve the internal state and thus you can't predict future random numbers, neither retrieve past ones.

If the function \(f\) is one-way as well, retrieving the internal state doesn't allow you to retrieve past state and thus past random numbers generated by the PRNG. This makes the PRNG forward-secure.

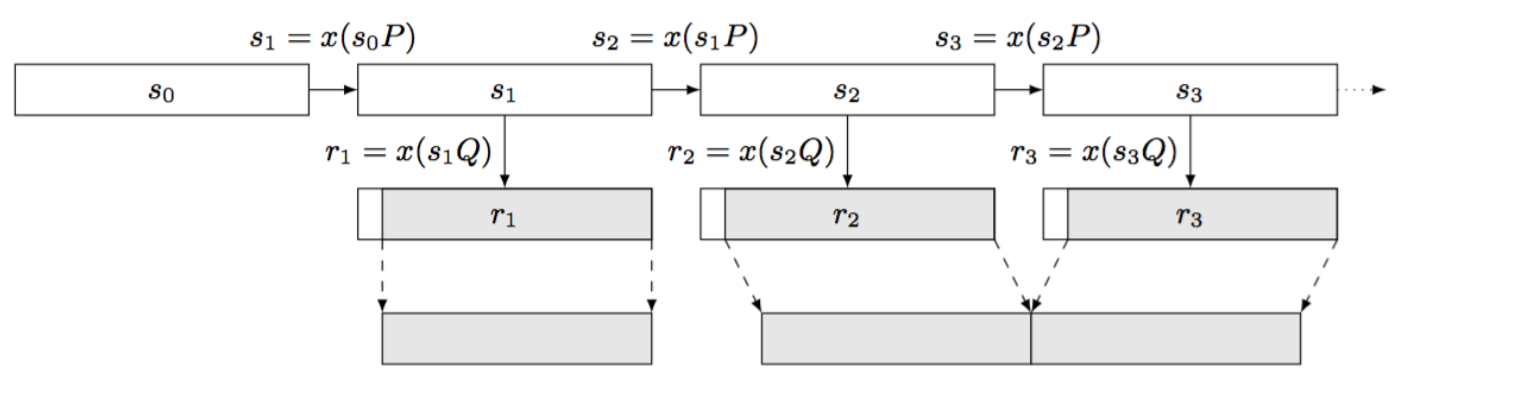
This is Dual EC. Iterating the state is done by multiplying the current state with the point \(P\) and then taking it's \(x\)-th coordinate. The point \(P\) is a point on a curve, with \(x\) and \(y\) coordinates, multiplying it with an integer gives us a new point on the curve. This is a one-way function because of the elliptic curve discrete logarithm problem and thus our PRNG is forward-secure (the ECDLP states that if you know \(P\) and \(Q\) in \(P = dQ\), it's really hard to find \(d\)).

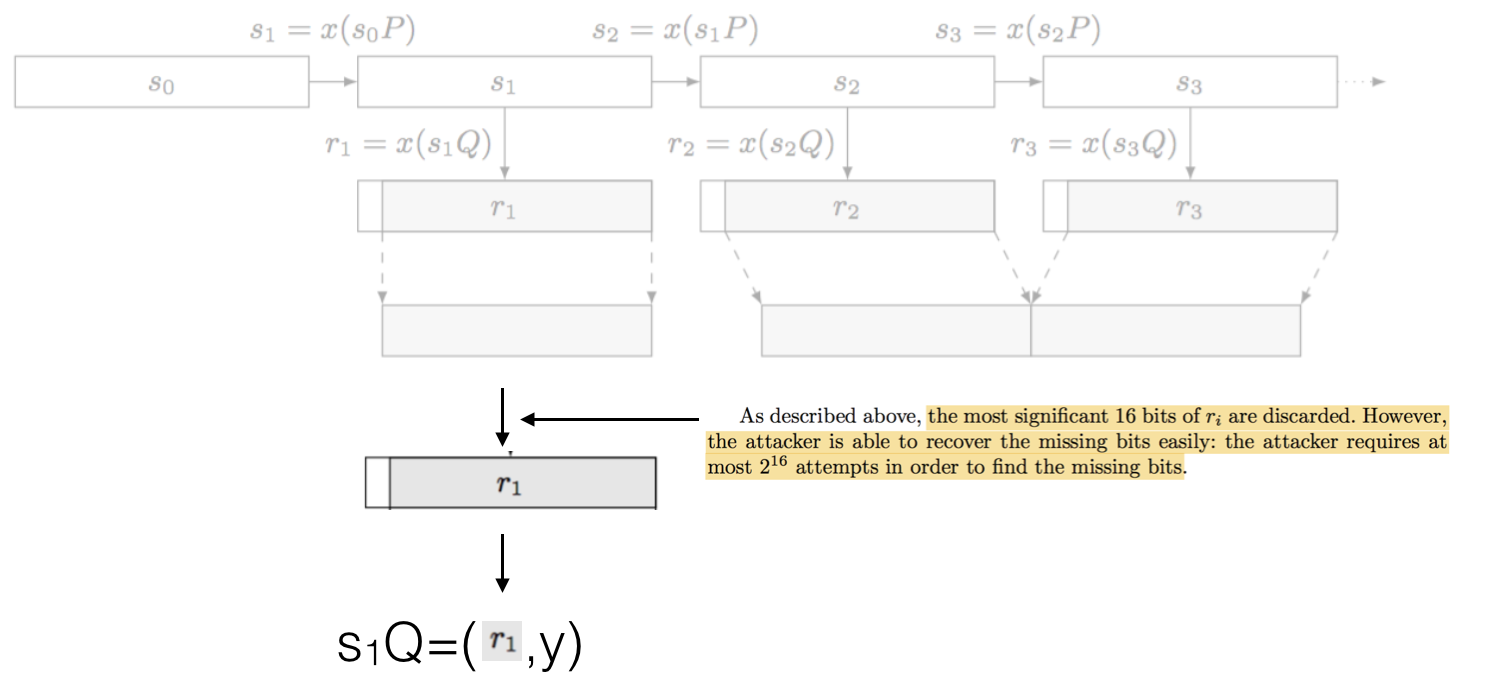
The interesting thing is that, in the attacker knows the secret integer \(d\) he can recover the next internal state of the PRNG. First, as seen above, the attacker recovers one random output, and then tries to get the full output: the real random output is done by truncating the first 16 bits of the full output. This is done in \(2^16\) iterations. Easy.

With our random number \(r_1\) (in our example), which is the \(x\) coordinate of our point \(s_1 Q\), we can easily recover the \(y\) coordinate and thus the entire point \(s_1 Q\). This is because of how elliptic curves are shaped.

Multiplying this point with our secret value \(d\) we obtain the next internal state as highlighted at the top of this picture:

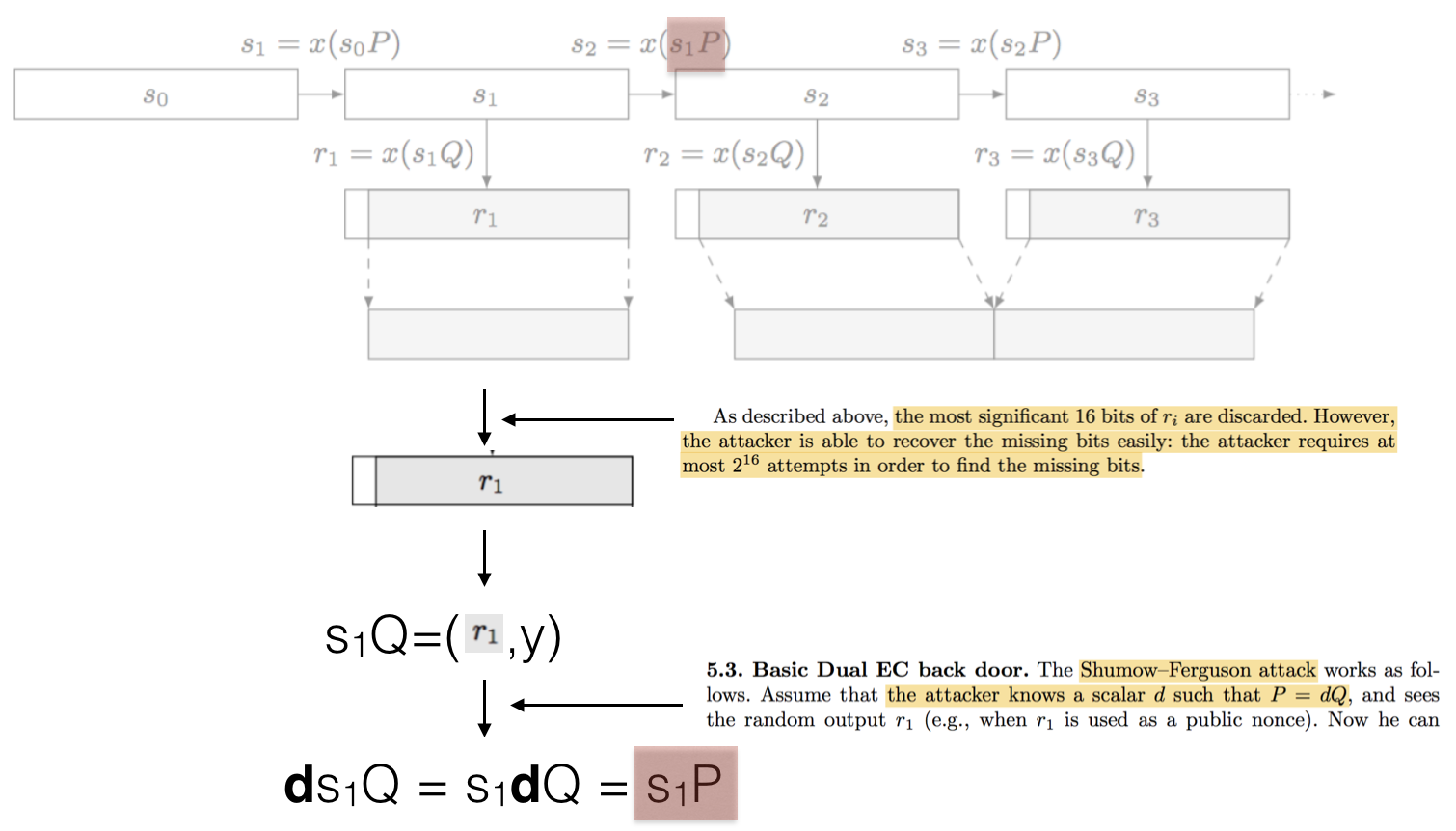
This attack is pretty destructive and in the order of mere minutes according to Dan Bernstein et al

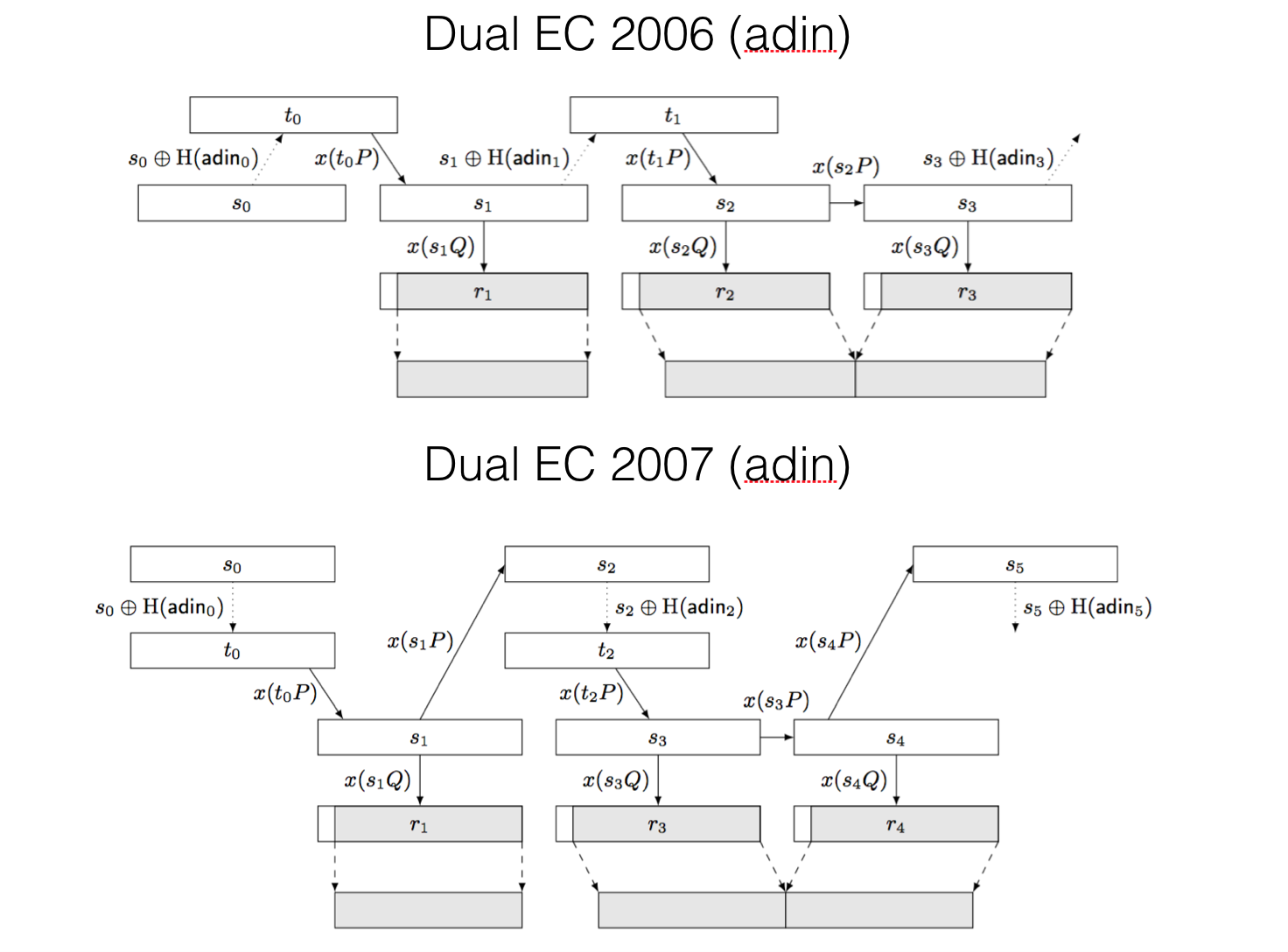
For completeness, it is important to know that there were two other constructions of the Dual EC PRNG with additional inputs, that allowed to add entropy to the internal state and thus provide backward secrecy: retrieving the internal state doesn't allow you to retrieve future states.

The first construction in 2006 broke the backdoor, the second in 2007 re-introduced it. Go figure...