Difference between shamir secret sharing (SSS) vs Multisig vs aggregated signatures (BLS) vs distributed key generation (dkg) vs threshold signatures posted December 2019

That title is a mouthful! But so is the field.

Let me introduce the problem: Alice owns a private key which can sign transactions. The problem is that she has a lot of money, and she is scared that someone will target her to steal all of her funds.

Cryptography offers some solutions to avoid this being a key management problem.

The first one is called Shamir Secret Sharing (SSS), which is simply about splitting the signing private key into n shares. Alice can then split the shares among her friends. When Alice wants to sign a transaction, she would then have to ask her friends to give her back the shares, that she can use to recreate the signing private key. Note that SSS has many many variants, for example VSSS allows participants to verify that malicious shares are not being used, and PSSS allows participants to proactively rotate their shares.

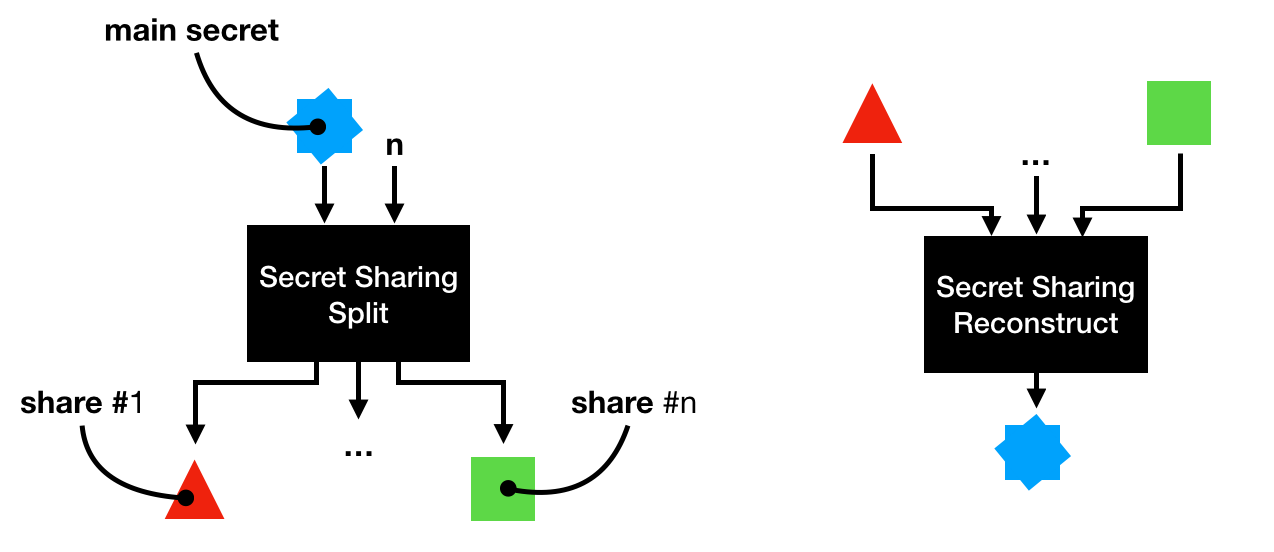
This is not great though, as there is a small timeframe in which Alice is the single point of failure again (the moment she holds all the shares).

A logical next step is to change the system, so that Alice cannot sign a transaction by herself. A multi-signature system (or multisig) would require n participants to sign the same transaction and send the n signatures to the system. This is much better, except for the fact that n signatures means that the transaction size increases linearly with the number of signers required.

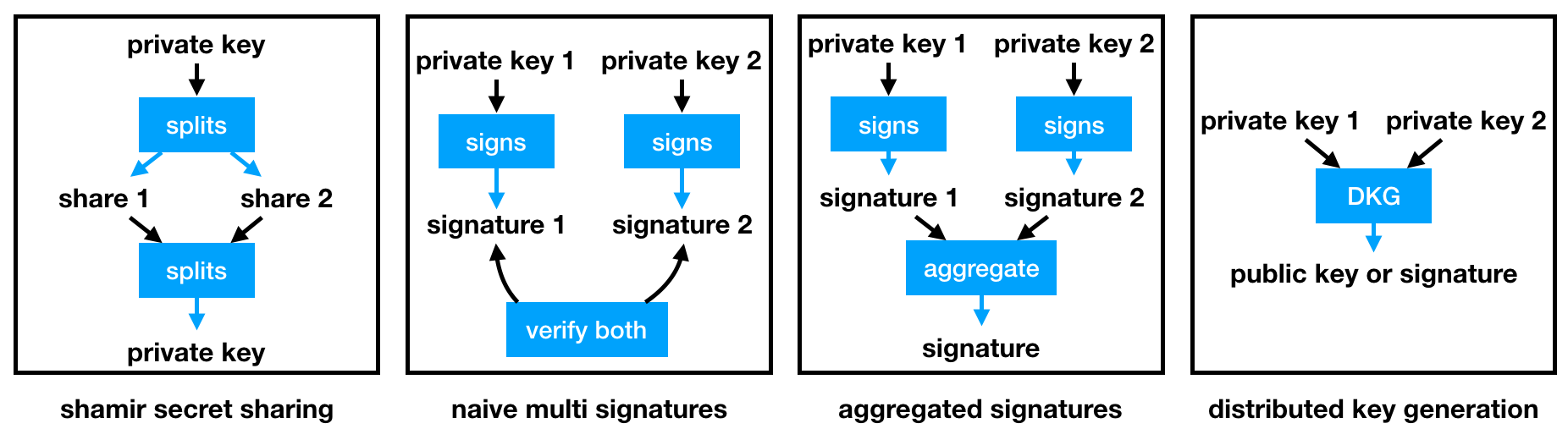
We can do better: a multi-signature system with aggregated signatures. Signature schemes like BLS allow you to compress the n signatures in a single signature. Note that it is currently much slower than popular signature schemes like ECDSA and EdDSA, so there must be a trade off between speed and size.

We can do even better though!

So far one still has to maintain a set of n public keys so that a signature can be verified. Distributed Key Generation (DKG) allows a set of participant to collaborate on the construction of a key pair, and on signing operations. This is very similar to SSS, except that there is never a single point of failure. This makes DKG a Multi-Party Computation (MPC) algorithm.

The BLS signature scheme can also aggregate public keys into a single key that will verify their aggregated signatures, which allows the construction of a DKG scheme as well.

Interestingly, you can do this with schnorr signatures too! The following diagram explains a simplified version of the scheme:

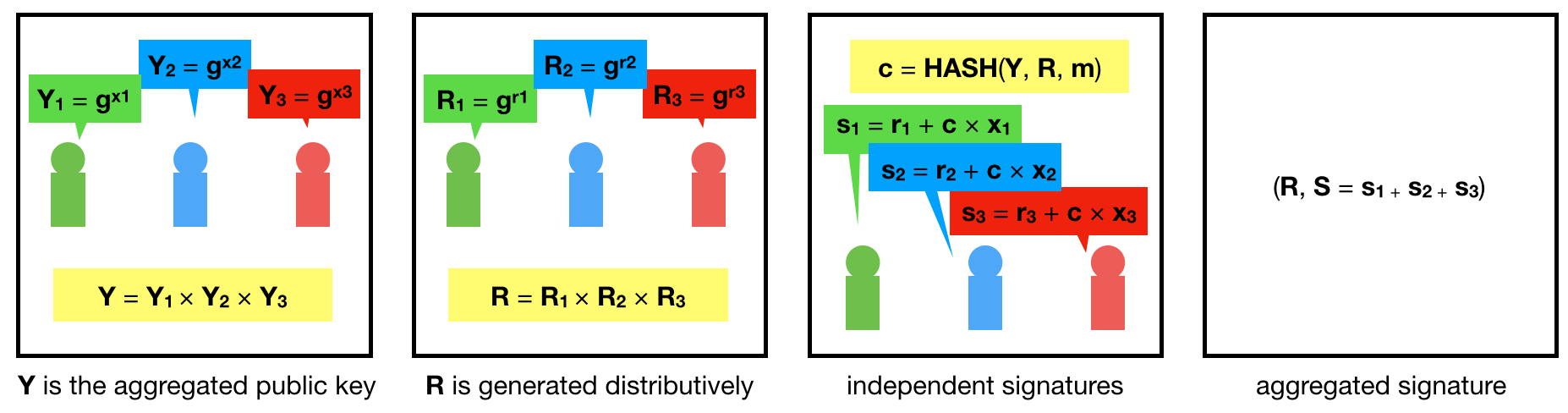
Note two things:

• All these schemes can be augmented to become threshold schemes: we don't need n signatures from the n signers anymore, but only a threshold m of n. (Having said that, when people talk about threshold signatures, they often mean the threshold version of DKG.) This way if someone loses their keys, or is on holiday, we can still sign.
• Most of these schemes assume that all participants are honest and by default don't tolerate malicious participants. More complicated schemes made to tolerate malicious participants exist.

Unfortunately all of this is pretty new, and as an active field of study no standard has been decided on one algorithm so far.

That's the difference!

One last thing: there's been some recent ideas to use zero knowledge proofs (ZKP) to do what aggregated signatures do but for multiple messages (because all the previous solutions all signed the same message). The idea is to release a proof that you have verified all the signatures associated to a set of messages. If the zero knowledge proof is shorter than all the signatures, it did its job!

did you like this? This will part of a book on cryptography! Check it out here.

EDIT: thanks to Dowhile and bascule for pointing errors in the post.