What's a symmetric password-authenticated key exchange (sPAKE) and how does SPAKE2 work? posted February 2020
have you heard of sPAKE (or bPAKE)?
a sPAKE is first and foremost a PAKE, which stands for Password-Authenticated Key Exchange. This simply means that authentication in the key exchange is provided via the knowledge of a password. The s (resp. b) in front means symmetric (resp. balanced). This indicates that both sides know the password.

Other PAKEs where only one side knows the password exist, these are called aPAKE for asymmetric (or augmented) PAKEs. Yes I know the nomenclature is a bit confusing :)
The most promising sPAKE scheme currently seems to be SPAKE2, which is in the process of being standardized here. There are other sPAKEs, like Dragonfly which is used in WPA3, but they don't seem to provide as strong properties as SPAKE2.
The trick to a symmetric PAKE is to use the password to blind the key exchange's ephemeral keypairs.
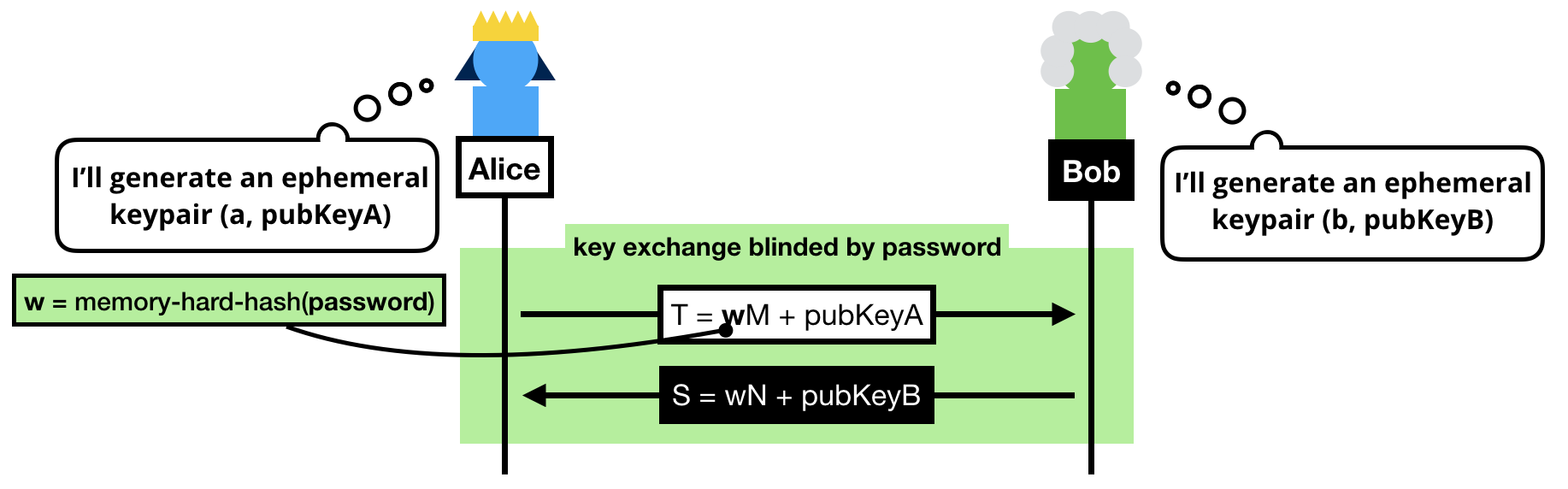
Note that we can't use the password as is, instead we:
- Pass the password into a memory-hard hash function like Argon2 to obtain
w. Can you guess why we do this? (leave a comment if you do!) - Convert it to a group element. To do this we simply consider
wa scalar and do a scalar multiplication with a generator of our subgroup (MorNdepending if you're the client or the server, can you guess why we use different generators?)
NOTE: If you know BLS or OPAQUE, you might be wondering why we don't use a "hash-to-curve" algorithm, this is because we don't need to obtain a group element with an unknown discrete logarithm in SPAKE2.
Once the blinded (with the password) public keys have been exchanged, both sides can compute a shared group element:
- Alice computes
K = h × alice_private_key × (S - w × N) - Bob computes
K = h × bob_private_key × (T - w × M)
Spend a bit of your time to understand these equations.
What happens is that both Alice and Bob first unblind the public key they've received, then perform a key exchange with it, then multiply it with the value h. What's this value h? The cofactor, or simply put: the other annoying subgroup.
Finally Alice and Bob hash the whole transcript, which is the concatenation of:
- Alice's identity.
- Bob's identity.
- The message Bob sent
S. - The message Alice sent
T. - The shared group element
K. - The hardened password
w.
The hash of this transcript gives us two things:
- A shared secret !
- A key that is further expanded (via a KDF) to obtain two authentication keys.
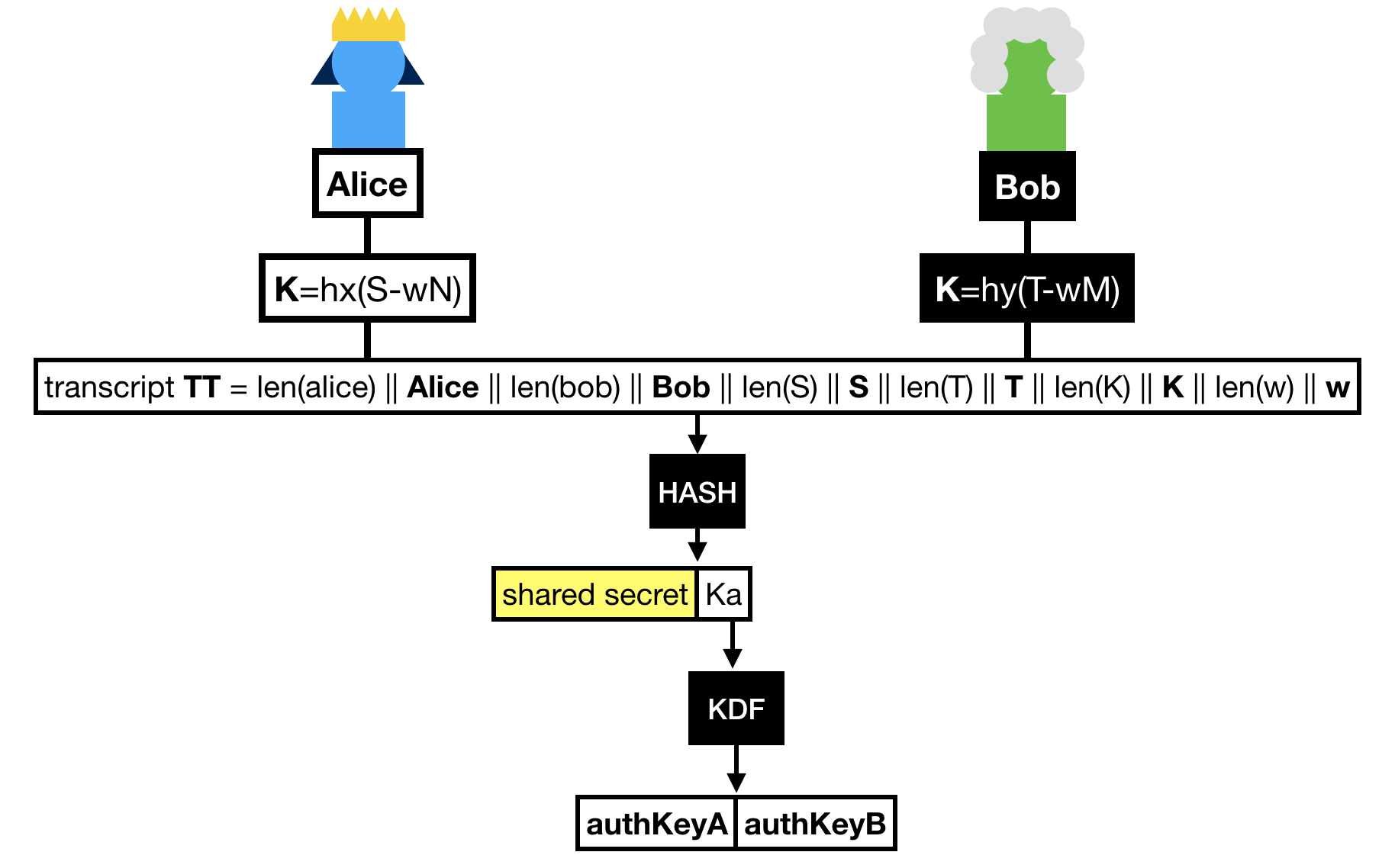
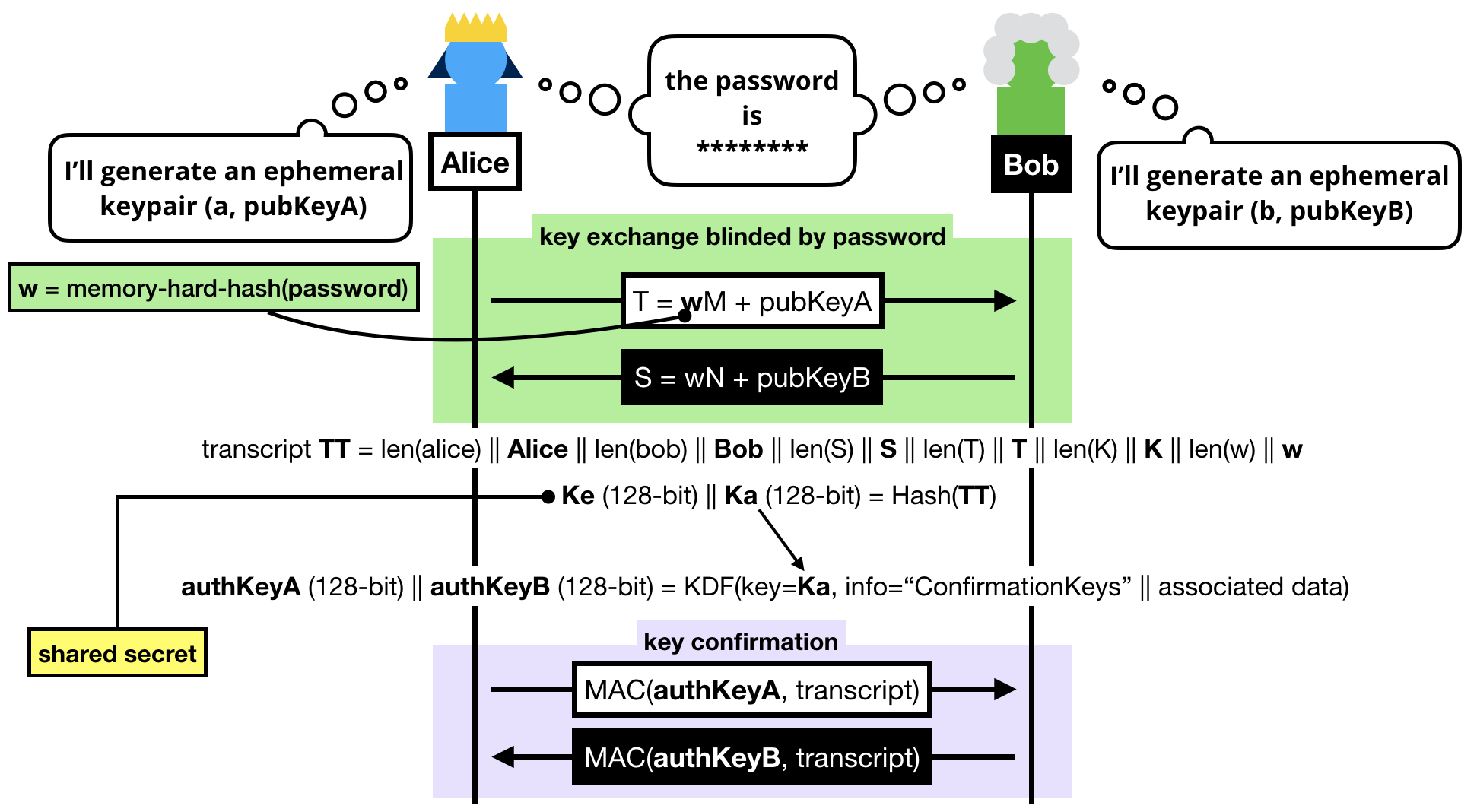
These authentication keys sole purpose is to provide key confirmation in the last round-trip of messages. That is to say at this point, if we don't do anything, we don't know if either Alice or Bob truly managed to compute the shared secret.
Key confirmation is pretty simple, both sides just have to compute an authentication tag with one of the authentication key produced over the transcript.
The final protocol looks a bit dense, but you should be able to decipher it if you've read this far.


Comments
dhg
Thank you for sharing, very concise.
Michael R.
Nice post! This is a surprisingly understandable protocol. Here are my answers to you questions to the audience:
1. We use a memory-hard hash function on the blinding factor because that's one way of stopping a brute force attack. The attack works by initiating a bunch of sessions with the server, trying a new w for each session. As soon as a session succeeds, the attacker learns that that's the password. Another way to prevent this is by instituting rate limiting on the server side, although that comes with its own downsides. Notably, this does not translate into an offline attack for a passive adversary, because a passive adversary would have no way of verifying their guess at the password if they don't know either side's secret key.
2. I was stumped on this one so I cheated. This is subtle. The current scheme relies on the Gap-Diffie-Hellman assumption: given (g^x, g^y) (with x,y chosen randomly) it is hard to compute g^(xy), even with access to an oracle that tells you if a triple (a,b,c) is a Diffie-Hellman triple. So if we set M=N in the above scheme, then the problem we have to rely on is the (weaker) Square-Gap-Diffie-Hellman assumption: given g^x (with x chosen randomly), it is hard to compute g^(x^2), even with access to an oracle that tells you if a triple (a,b,c) is a Diffie-Hellman triple. I don't know of any instances where the latter problem is noticeably easier than the former. Are there any out there?
Hajeur
Well explained!
Thanks
leave a comment...