The Let's Encrypt duplicate signature key selection attack posted March 2021

On August 11th, 2015, Andrew Ayer sent an email to the IETF mailing list starting with the following words:

I recently reviewed draft-barnes-acme-04 and found vulnerabilities in the DNS, DVSNI, and Simple HTTP challenges that would allow an attacker to fraudulently complete these challenges.

The draft-barnes-acme-04 mentioned by Andrew Ayer is a document specifying ACME, one of the protocols behind the Let's Encrypt certificate authority. A certificate authority is the thing that your browser trusts and that signs the public keys of websites you visit. It is called a "certificate" authority due to the fact that it does not sign public keys, but certificates. A certificate is just a blob of data bundling a website's public key, its domain name, and some other relevant metadata.

The attack was found merely 6 weeks before major browsers were supposed to start trusting Let's Encrypt's public key. The draft has since become RFC 8555: Automatic Certificate Management Environment (ACME), mitigating the issues. Since then no cryptographic attacks are known on the protocol.

This blog post will go over the accident, and explain why it happened, why it was a surprising bug, and what you should watch for when using signatures in cryptography.

How Let's Encrypt used signatures

Let's Encrypt is a pretty big deal. Created in 2014, it is a certificate authority run as a nonprofit, providing trust to hundreds of millions of websites.

The key to Let's Encrypt's success are twofold:

• It is free. Before Let's Encrypt most certificate authorities charged fees from webmasters who wanted to obtain certificates.
• It is automated. If you follow their standardized protocol, you can request, renew and even revoke certificates via a web interface. Contrast that to other certificate authorities who did most processing manually, and took time to issue certificates.

If a webmaster wants her website example.com to provide a secure connection to her users (via HTTPS), she can request a certificate from Let's Encrypt (essentially a signature over its domain name and public key), and after proving that she owns the domain example.com and getting her certificate issued, she will be able to use it to negotiate a secure connection with any browser trusting Let's Encrypt.

That's the theory.

In practice the flow goes like this:

1. Alice registers on Let's Encrypt with an RSA public key.
2. Alice asks Let's Encrypt for a certificate for example.com.
3. Let's Encrypt asks Alice to prove that she owns example.com, for this she has to sign some data and upload it to example.com/.well-known/acme-challenge/some_file.
4. Once Alice has signed and uploaded the signature, she asks Let's Encrypt to go check it.
5. Let's Encrypt checks if it can access the file on example.com, if it successfully downloaded the signature and the signature is valid then Let's Encrypt issues a certificate to Alice.

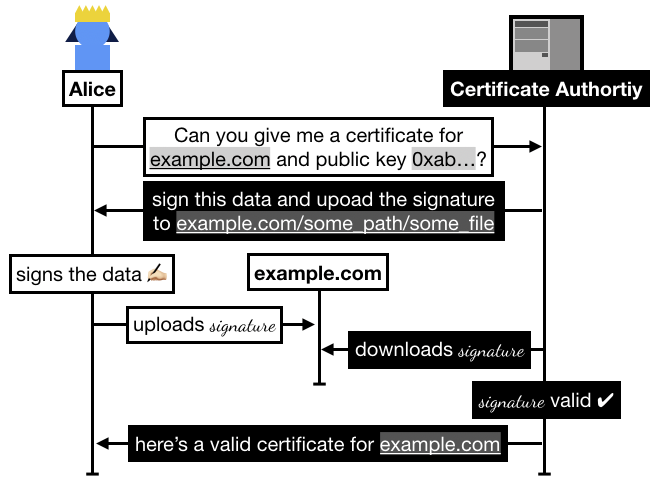
In 2015, Alice could request a signed certificate from Let's Encrypt by uploading a signature (from the key she registered with) on her domain. The certificate authority verifies that Alice owns the domain by downloading the signature from the domain and verifying it. If it is valid, the authority signs a certificate (which contains the domain's public key, the domain name example.com, and some other metadata) and sends it to Alice who can then use it to secure her website in a protocol called TLS.

Let's see next how the attack worked.

How did the Let's Encrypt attack work?

In the attack that Andrew Ayer found in 2015, Andrew proposes a way to gain control of a Let's Encrypt account that has already validated a domain (let's pick example.com as an example)

The attack goes something like this (keep in mind that I'm simplifying):

1. Alice registers and goes through the process of verifying her domain example.com by uploading some signature over some data on example.com/.well-known/acme-challenge/some_file. She then successfully manages to obtain a certificate from Let's Encrypt.
2. Later, Eve signs up to Let's Encrypt with a new account and an RSA public key, and request to recover the example.com domain
3. Let's Encrypt asks Eve to sign some new data, and upload it to example.com/.well-known/acme-challenge/some_file (note that the file is still lingering there from Alice's previous domain validation)
4. Eve crafts a new malicious keypair, and updates her public key on Let's Encrypt. She then asks Let's Encrypt to check the signature
5. Let's Encrypt obtains the signature file from example.com, the signature matches, Eve is granted ownership of the domain example.com. She can then ask Let's Encrypt to issue valid certificates for this domain and any public key.

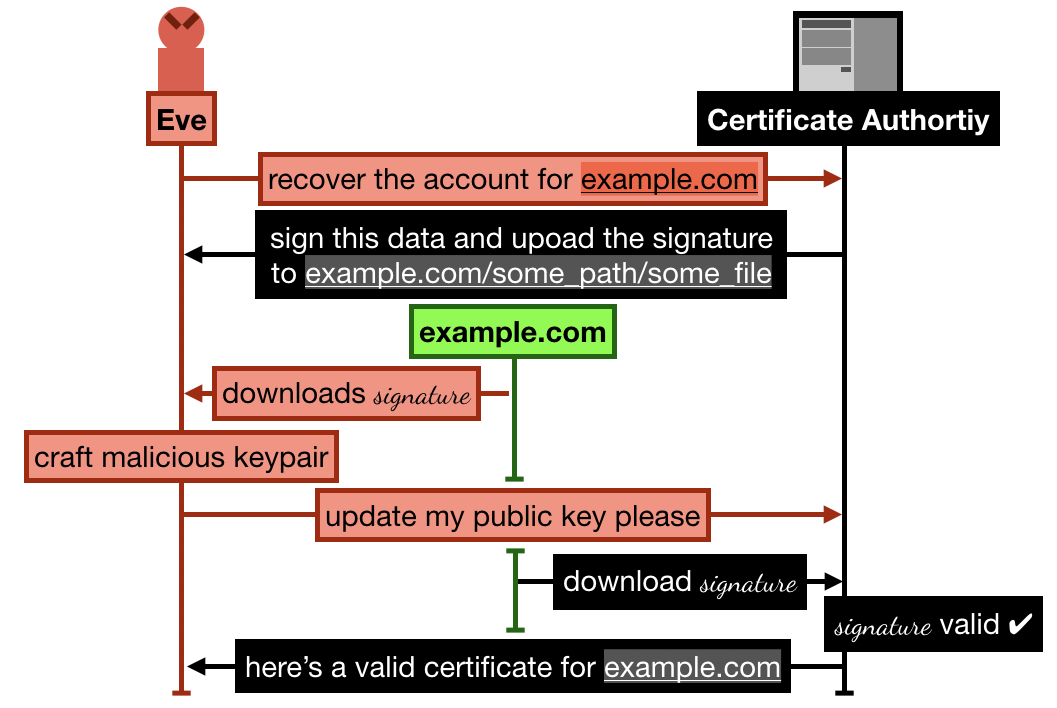
The 2015 Let's Encrypt attack allowed an attacker (here Eve) to successfully recover an already approved account on the certificate authority. To do this, she simply forges a new keypair that can validate the already existing signature and data from the previous valid flow.

Take a few minutes to understand the attack. It should be quite surprising to you. Next, let's see how Eve could craft a new keypair that worked like the original one did.

Key substitution attacks on RSA

In the previously discussed attack, Eve managed to create a valid public key that validates a given signature and message. This is quite a surprising property of RSA, so let's see how this works.

A digital signature does not uniquely identify a key or a message. -- Andrew Ayer, Duplicate Signature Key Selection Attack in Let's Encrypt (2015)

Here is the problem given to the attacker: for a fixed signature and (PKCS#1 v1.5 padded) message, a public key $(e, N)$ must satisfy the following equation to validate the signature:

$$signature = message^e \pmod{N}$$

One can easily craft a key pair that will (most of the time) satisfy the equation:

• a public exponent $e = 1$
• a private exponent $d = 1$
• a public modulus $N = \text{signature} - \text{message}$

You can easily verify that the validation works with this keypair:

$$\begin{align} &\text{signature} = \text{message}^e \mod{N} \\ \iff &\text{signature} = \text{message} \mod{\text{signature} - \text{message}} \\ \iff &\text{signature} - \text{message} = 0 \mod{\text{signature} - \text{message}} \end{align}$$

Is this issue surprising?

It should be.

This property called "key substitution" comes from the fact that there exists a gap between the theoretical cryptography world and the applied cryptography world, between the security proofs and the implemented protocols.

Signatures in cryptography are usually analyzed with the EUF-CMA model, which stands for Existential Unforgeability under Adaptive Chosen Message Attack.

In this model YOU generate a key pair, and then I request YOU to sign a number of arbitrary messages. While I observe the signatures you produce, I win if I can at some point in time produce a valid signature over a message I hadn't requested.

Unfortunately, even though our modern signature schemes seem to pass the EUF-CMA test fine, they tend to exhibit some surprising properties like the key substitution one.

To learn more about key substitution attack and other signature shenanigans, take a look at my book Real-World Cryptography.