Quick access to articles on this page:
more on the next page...
I read a Why Not Rust? article the other day that was quite good but dismissed the most important reason to use a language to me: security. After having worked on a Rust codebase for almost two years now, I thought I would chime in, even though I'll preface the post by saying that Rust is totally the right language you should use if you know what you're doing and are aiming for performance and security, yet I still have some pain points that will make me recommend Golang over Rust sometimes. Keep in mind that I have also spent my whole career looking for bugs in applications written in dozens of different languages, so my post might be highly controversial but it has to be looked from these lenses.
Shallow standard library
Working with Rust is like working with Javascript in many ways. While the package manager Cargo is truly awesome, the fact that the standard library misses most features will have you import many third-party dependencies. These dependencies in turn import other third-party dependencies, that import other third-party dependencies, and so on. This blow up of dependencies can quickly become a nightmare, and this is of course a perfect vector of attack for backdoors, like we've seen happen before in javascript land (https://www.infoq.com/news/2018/05/npm-getcookies-backdoor/, https://www.zdnet.com/article/hacker-backdoors-popular-javascript-library-to-steal-bitcoin-funds/).
Not only this, but if you're a newcomer to Rust, how do you even pick the right library? I can't even fathom how anyone writing a project in Rust gets to pick a good library for generating cryptographic random numbers, or for doing any type of crypto like encrypting or hashing, or for decoding hex strings, or for decoding JSON, or for using TCP, or even for using TLS! On the other hand Golang has all of that in its standard library, that means that when you use Golang you:
- can't pick the wrong algorithm (e.g. DES instead of AES)
- can't pick a bad implementation (the standard library is known to be high quality)
- can't pick a dependency that ends up importing plenty of other third-party dependencies (unlike Rust, the Golang standard library never imports third-party libraries)
- don't have to worry about version updates (you're just updating your version of Golang instead of the versions of many dependencies)
- don't have to worry about transitive dependencies that you can't update (again, Golang standard library doesn't rely on third-party dependencies)
For Libra we've used a number of techniques in order to reduce the number of third-party dependencies we use. This included figuring out when we used different dependencies that did the same thing, or figuring out what obscure dependencies we should avoid, we even re-wrote a large number of dependencies to avoid dependencies that ended up exploding the number of transitive third-party dependencies we imported. One useful tool we used for some of that is dephell which is built on top of guppy.
Rustfmt is imperfect
rustfmt is great, but rustfmt sucks. Why does it suck? Two reasons:
- it's not mandatory
- it's configurable
On the other hand, Golang's compiler is very strict and will yell at you early on if you have dead code, unused dependencies, badly formatted code, and so on. It doesn't replace gofmt, but it's much more opinionated and is much more effective at making Golang's codebases more readable (especially if they forget to run gofmt). In addition, if you do use gofmt, you can't configure it! This is very apparent when you read Golang code, it always looks the same! And it is pretty fucking fantastic if you ask me, because not only Golang is easy to learn, but you can quickly get used to any Golang codebase due to the consistent formatting of the language.
Too many ways to do things
Rust has a somewhat different syntax from other languages of its genre, and you sometimes see things that you might not be used to see (statement as expression, match statements, lifetimes, etc.) I couldn't care less about these, these are things you can learn, and you end up getting used to them. What I can't get used to is the sheer number of ways to do something. There are so many keywords in Rust, and there's so many ways to end up bike shedding on the best way to write the exact same statement, that I consider it a waste of time. It's a waste of time for the developers, but also for the reviewers who will often run into keywords that they've never seen before. For example, there are too many ways to panic on purpose: panic!(), unwrap(), except(), unreachable!(), todo!(), unimplemented!(), assert!(), and so on.
Generics and macros
Rust is too expressive. This is of course great for some use-cases, but holy shit if a developer wants to be too clever, they can create the most unintelligible codebase that you'll ever seen. This is probably the most controversial point, but security is not just safety, it's also readability. As we say "complexity is the enemy of security", and generics undeniably add complexity. This is of course up to the developers to abuse them, but the great thing about Golang is that there aren't many things to abuse, codebases are often straight forward and you can quickly understand what is happening.
Ok, you're being unreasonable David
Sure, I'm omitting a lot of good Rust things in here, but this is a post about the security downsides of Rust, not the upsides, which let's be clear still make Rust the perfect language to write a sensitive application in. You just need to know what you're doing. This also means that Rust has a lot of room to mature, while generics are here to stay, there is no excuse to keep slipping the shallow stdlib under the rug.
I’ve now been writing a book on applied cryptography for a year and a half.
I’m nearing the end of my journey, as I have one last ambitious chapter left to write: next-generation cryptography (a chapter that I’ll use to talk about cryptography that will become more and more practical: post-quantum cryptography, homomorphic encryption, multi-party computation, and zk-SNARKs).
I’ve been asked multiple times why write a new book about cryptography? and why should I read your book?.
To answer this, you have to understand when it all started…
A picture is worth a thousand words
Today if you want to learn about almost anything, you just google it.
Yet, for cryptography, and depending on what you're looking for, resources can be quite lacking.
It all started a long time ago.
For a class, I had to implement a differential power analysis attack, a breakthrough in cryptanalysis as it was the first side-channel attack to be published.
A differential power analysis uses the power consumption of a device during an encryption to leak its private key.
At the time, I realized that great papers could convey great ideas with very little emphasis on understanding.
I remember banging my head against the wall trying to figure out what the author of the white paper was trying to say.
Worse, I couldn’t find a good resource that explained the paper.
So I banged my head a bit more, and finally I got it.
And then I thought I would help others.
So I drew some diagrams, animated them, and recorded myself going over them.
That was my first screencast.
This first step in education was enough to make me want to do more.
I started making more of these videos, and started writing more articles about cryptography on this blog (today totaling more than 500 articles).
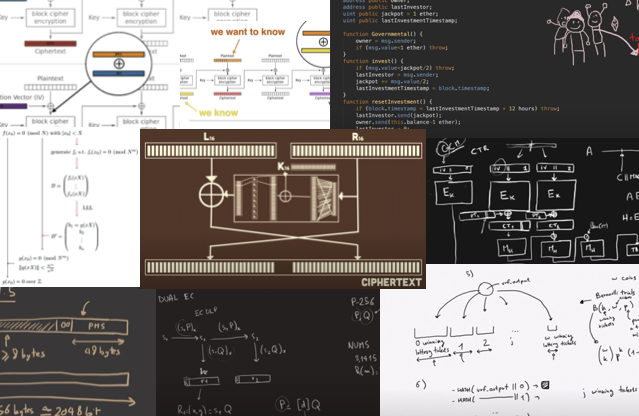
I realized early that diagrams were extremely helpful to understand complicated concepts, and that strangely most resources in the field shied away from them.
For example, anyone in cryptography who thinks about AES-CBC would immediately think about the following wikipedia diagram:
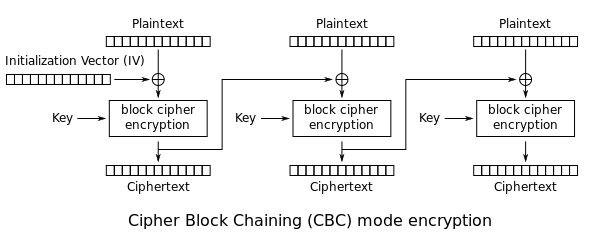
So here I was, trying to explain everything I learned, and thinking hard about what sorts of simple diagrams could easily convey these complex ideas.
That’s when I started thinking about a book, years and years before Manning Publications would reach out to me with a book deal.
The applied cryptographer curriculum
I hadn’t started cryptography due to a long-life passion.
I had finished a bachelor in theoretical mathematics and didn’t know what was next for me.
I had also been programming my whole life, and I wanted to reconcile the two.
Naturally, I got curious about cryptography, which seemed to have the best of both world, and started reading the different books at my disposal.
I quickly discovered my life's calling.
Some things were annoying me though. In particular, the long introductions that would start with history.
I was only interested in the technicalities, and always had been.
I swore to myself, if I ever wrote a book about cryptography, I would not write a single line on Vigenère ciphers, Caesar ciphers, and others.
And so after applying to the masters of Cryptography at the university of Bordeaux, and obtaining a degree in the subject, I thought I was ready for the world.
Little did I know.
What I thought was a very applied degree actually lacked a lot on the real world protocols I was about to attack.
I had spent a lot of time learning about the mathematics of elliptic curves, but nothing about how they were used in cryptographic algorithms.
I had learned about LFSRs, and ElGamal, and DES, and a series of other cryptographic primitives that I would never see again.
When I started working in the industry at Matasano, which then became NCC Group, my first gig was to audit OpenSSL (the most popular TLS implementation).
Oh boy, did it hurt my brain.
I remember coming back home every day with a strong headache.
What a clusterfuck of a library.
I had no idea at the time that I would years later become a co-author of TLS 1.3.

But at that point I was already thinking: this is what I should have learned in school.
The knowledge I’m getting now is what would have been useful to prepare me for the real world.
After all, I was now a security practitioner specialized in cryptography.
I was reviewing real-world cryptographic applications.
I was doing the job that one would wish they had after finishing a cryptography degree.
I implemented, verified, used, and advised on what cryptographic algorithms to use.
This is the reason I’m the first reader of the book I’m writing.
This is what I would have written to my past self in order to prepare me for the real world.
The use of cryptography is where most of the bugs are
My consulting job led me to audit many real world cryptographic applications like the OpenSSL, the encrypted backup system of Google, the TLS 1.3 implementation of Cloudflare, the certificate authority protocol of Let’s Encrypt, the sapling protocol of Zcash, the threshold proxy re-encryption scheme of NuCypher and dozens and dozens of other real-world cryptographic applications that I unfortunately cannot mention publicly.
Early in my job, I was tasked to audit the custom protocol a big corporation (that I can’t name) had written to encrypt their communications.
It turns out that, they were signing everything but the ephemeral keys, which completely broke the whole protocol (as one could have easily replaced the ephemeral keys).
A rookie mistake from anyone with some experience with secure transport protocols, but something that was missed by people who thought they were experienced enough to roll their own crypto.
I remember explaining the vulnerability at the end of the engagement, and a room full of engineers turning silent for a good 30 seconds.
This story repeated itself many times during my career.
There was this time where while auditing a cryptocurrency for another client, I found a way to forge transactions from already existing ones (due to some ambiguity of what was being signed).
Looking at TLS implementations for another client, I found some subtle ways to break an RSA implementation, which in turned transformed into a white paper (with one of the inventor of RSA) leading to a number of Common Vulnerabilities and Exposures (CVEs) reported to a dozen of open source projects.
More recently, reading about Matrix as part of writing my book, I realized that their authentication protocol was broken, leading to a break of their end-to-end encryption.

There’s so many details that can unfortunately collapse under you, when making use of cryptography.
At that point, I knew I had to write something about it.
This is why my book contains many of these anecdotes.
As part of the job, I would review cryptography libraries and applications in a multitude of programming languages.
I discovered bugs (for example CVE-2016-3959 in Golang’s standard library), I researched ways that libraries could fool you into misusing them (for example see my paper How to Backdoor Diffie-Hellman), and I advised on what libraries to use.
Developers never knew what library to use, and I always found the answer to be tricky.
I went on to invent the disco protocol, and wrote a fully-featured cryptographic library in less than 1,000 lines of code in several languages.
Disco only relied on two cryptographic primitives: the permutation of SHA-3 and curve25519.
Yes, from only these two things in 1,000 lines of code a developer could do any type of authenticated key exchange, signatures, encryption, MACs, hashing, key derivation, etc.
This gave me a unique perspective as to what a good cryptographic library was supposed to be.
I wanted my book to contain these kind of practical insights.
So naturally, the different chapters contain examples on how to do crypto in different programming languages, using well-respected cryptographic libraries.
A need for a new book?
As I was giving one of my annual cryptography training at Black Hat, one student came to me and asked if I could recommend a good book or online course on cryptography.
I remember advising the student to read the book from Boneh & Shoup and Cryptography I from Boneh on Coursera.
The student told me “Ah, I tried, it’s too theoretical!”.
This answer stayed with me.
I disagreed at first, but slowly realized that they were right.
Most of these resources were pretty heavy in math, and most developers interacting with cryptography don’t want to deal with math.
What else was there for them?
The other two somewhat respected resources at the time were Applied Cryptography and Cryptography Engineering (both from Schneier).
But these books were starting to be quite outdated.
Applied Cryptography spent 4 chapters on block ciphers, with a whole chapter on cipher modes of operation but none on authenticated encryption.
Cryptography Engineering had a single mention of elliptic curve cryptography (in a footnote).
On the other hand, many of my videos or blog posts were becoming good primary references for some cryptographic concepts.
I knew I could do something special.
Gradually, many of my students started becoming interested in cryptocurrencies, asking more and more questions on the subject.
At the same time, I started to audit more and more cryptocurrency applications.
I finally moved to a job at Facebook to work on Libra.
Cryptocurrency was now one of the hottest field to work on, mixing a multitude of extremely interesting cryptographic primitives that so far had seen no real-world use case (zero knowledge proofs, aggregated signatures, threshold cryptography, multi-party computations, consensus protocols, cryptographic accumulators, verifiable random functions, verifiable delay functions, ... the list goes on)
I was now in a unique position.
I knew I could write something that would tell students, developers, consultants, security engineers, and others, what modern applied cryptography was all about.

This was going to be a book with very little formulas, but filled with many diagrams.
This was going to be a book with little history, but filled with modern stories about cryptographic failures that I had witnessed for real.
This was going to be a book with little about legacy algorithms, but filled with cryptography that I've personally seen being used at scale: TLS, the Noise protocol framework, Wireguard, the Signal protocol, cryptocurrencies, HSMs, threshold cryptography, and so on.
This was going to be a book with little theoretical cryptography, but filled with what could become relevant: password-authentication key exchanges, zero-knowledge proofs, post-quantum cryptography, and so on.
Real-World Cryptography
When Manning Publications reached out to me in 2018, asking if I wanted to write a book on cryptography for them, I already knew the answer.
I already knew what I wanted to write about.
I had just been waiting for someone to give me the opportunity, the excuse to spend my time writting the book I had in mind.
Coincidentally, they had a series of "real-world" book, and so naturally I suggested that my book extend it.

Real-World Cryptography is available for free in early-access.
I want this to be the best book on applied cryptography.
For this reason, if you have any feedback to give, please send it my way :)
The book should be ready in print for the end of the year.
The Secure Remote Password (SRP) protocol is first and foremost a Password Authenticated Key Exchange (PAKE).
Specifically, SRP is an asymmetric or augmented PAKE: it’s a key exchange where only one side is authenticated thanks to a password. This is usually useful for user authentication protocols. Theoretically any client-server protocol that relies on passwords (like SSH) could be doing it, but instead such protocols often have the password directly sent to the server (hopefully on a secure connection). As such, asymmetric PAKEs offer an interesting way to augment user authentication protocols to avoid the server learning about the user’s password.
Note that the other type of PAKE is called a symmetric or balanced PAKE. In a symmetric PAKE two sides are authenticated thanks to the same password. This is usually useful in user-aided authentication protocols where a user attempts to pair two physical devices together, for example a mobile phone or laptop to a WiFi router. (Note that the recent WiFi protocol WPA3 uses the DragonFly symmetric PAKE for this.)
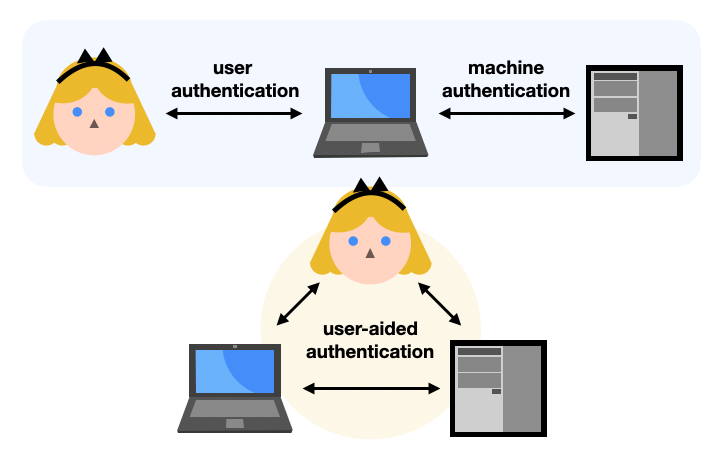
In this blog post I will answer the following questions:
- What is SRP?
- How does SRP work?
- Should I use SRP today?
What is SRP?
The stanford SRP homepage puts it in these words:
The Secure Remote Password protocol performs secure remote authentication of short human-memorizable passwords and resists both passive and active network attacks. Because SRP offers this unique combination of password security, user convenience, and freedom from restrictive licenses, it is the most widely standardized protocol of its type, and as a result is being used by organizations both large and small, commercial and open-source, to secure nearly every type of human-authenticated network traffic on a variety of computing platforms.
and goes on to say:
The SRP ciphersuites have become established as the solution for secure mutual password authentication in SSL/TLS, solving the common problem of establishing a secure communications session based on a human-memorized password in a way that is crytographically sound, standardized, peer-reviewed, and has multiple interoperating implementations. As with any crypto primitive, it is almost always better to reuse an existing well-tested package than to start from scratch.
But the Stanford SRP homepage seems to date from the late 90s.
SRP was standardized for the first time in 2000 in RFC 2944 - Telnet Authentication: SRP.
Nowadays, most people refer to SRP as the implementation used in TLS. This one was specified in 2007 in RFC 5054 - Using the Secure Remote Password (SRP) Protocol for TLS Authentication.
How does SRP work?
The Stanford SRP homage lists 4 different versions of SRP, with the last one being SRP 6. Not sure where version 4 and 5 are, but version 6 is the version that is standardized and implemented in TLS. There is also the revision SRP 6a, but I’m also not sure if it’s in use anywhere today.
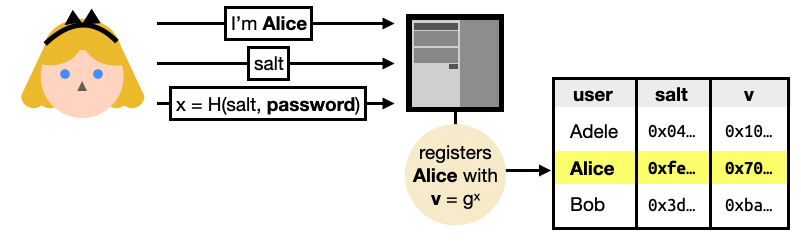
To register, Alice sends her identity, a random $salt$, and a salted hash $x$ of her password.
Right from the start, you can see that a hash function is used (instead of a password hash function like Argon2) and thus anyone who sees this message can efficiently brute-force the hashed password. Not great. The use of the user-generated salt though, manage to prevent brute-force attacks that would impact all users.
The server can then register Alice by exponentiating a generator of a pre-determined ring (an additive group with a multiplicative operation) with the hashed password. This is an important step as you will see that anyone with the knowledge of $x$ can impersonate Alice.
What follows is the login protocol:
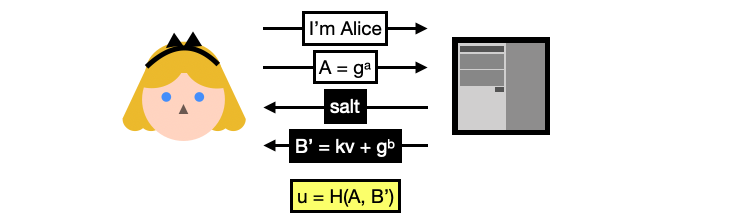
You can now see why this is called a password authenticated key exchange, the login flow includes the standard ephemeral key exchange with a twist: the server’s public key $B’$ is blinded or hidden with $v$, a random value derived from Alice’s password. (Note here $k$ is a constant fixed by the protocol so we will just ignore it.)
Alice can only unblinds the server’s ephemeral key by deriving $v$ herself. To do this, she needs the $salt$ she registered with (and this is why the server sends it back to Alice as part of the flow).
For Alice, the SRP login flow goes like this:
- Alice re-computes $x = H(salt, password)$ using her password and the salt received from the server.
- Alice unblinds the server’s ephemeral key by doing $B=B’- kg^x = g^b$
- Alice then computes the shared secret $S$ by multiplying the results of two key exchanges:
- $B^a$, the ephemeral key exchange
- $B^{ux}$, a key exchange between the server’s public key and a value combining the hashed password and the two ephemeral public keys
Interestingly, the second key exchange makes sure that the hashed password and the transcript gets involved in the computation of the shared secret. But strangely, only the public keys and not the full transcript are used.
The server can then compute the shared secret $S$ as well, using the multiplication of the same two key exchanges:
- $A^b$, the ephemeral key exchange
- $v^{ub}$, the other key exchange involving the hashed password and the two ephemeral public keys
The final step is for both sides to hash the shared secret and use it as the session key $K = H(S)$.
Key confirmation can then happen after both sides make successful use of this session key. (Without key confirmation, you’re not sure if the other side managed to perform the PAKE.)
Should I use SRP today?
The SRP scheme is a much better way to handle user passwords, but it has a number of flaws that make the PAKE protocol less than ideal. For example, someone who intercepts the registration process can then easily impersonate Alice as the password is never directly used in the protocol, but instead the salted hash of the password which is communicated during the registration process.
This was noticed by multiple security researchers along the years. Matthew Green in 2018 wrote Should you use SRP?, in which he says:
Lest you think these positive results are all by design, I would note that there are [five prior versions] of the SRP protocol, each of which contains vulnerabilities. So the current status seems to have arrived through a process of attrition, more than design.
After noting that the combination of multiplication and addition makes it impossible to implement in elliptic curve groups, Matthew Green concludes with:
In summary, SRP is just weird. It was created in 1998 and bears all the marks of a protocol invented in the prehistoric days of crypto. It’s been repeatedly broken in various ways, though the most recent [v6] revision doesn’t seem obviously busted — as long as you implement it carefully and use the right parameters. It has no security proof worth a damn, though some will say this doesn’t matter (I disagree with them.)
Furthermore, SRP is not available in the last version of TLS (TLS 1.3).
Since then, many schemes have been proposed, and even standardized and productionized (for example PAK was standardized by Google in 2010)
The IETF 104, March 2019 - Overview of existing PAKEs and PAKE selection criteria has a list:

In the summer of 2019, the Crypto Forum Research Group (CFRG) of the IETF started a PAKE selection process, with goal to pick one algorithm to standardize for each category of PAKEs (symmetric/balanced and asymmetric/augmented):

Two months ago (March 20th, 2020) the CFRG announced the end of the PAKE selection process, selecting:
- CPace as the symmetric/balanced PAKE (from Björn Haase and Benoît Labrique)
- OPAQUE as the asymmetric/augmented PAKE (from Stanislaw Jarecki, Hugo Krawczyk, and Jiayu Xu)
Thus, my recommendation is simple, today you should use OPAQUE!
If you want to learn more about OPAQUE, check out chapter 11 of my book real world cryptography.
As part of my book's chapter on end-to-end encryption I've been writing about the horrors of PGP.
As a recap of what's bad with PGP:
- No authenticated encryption. This is my biggest issue with PGP personally.
- Receiving a signed message means nothing about who sent it to you (see picture below).
- Usability issues with GnuPG (the main implementation).
- Discoverability of public keys issue.
- Bad integration with emails.
- No forward secrecy.
For more, see my post on a history of end-to-end encryption and the death of PGP.
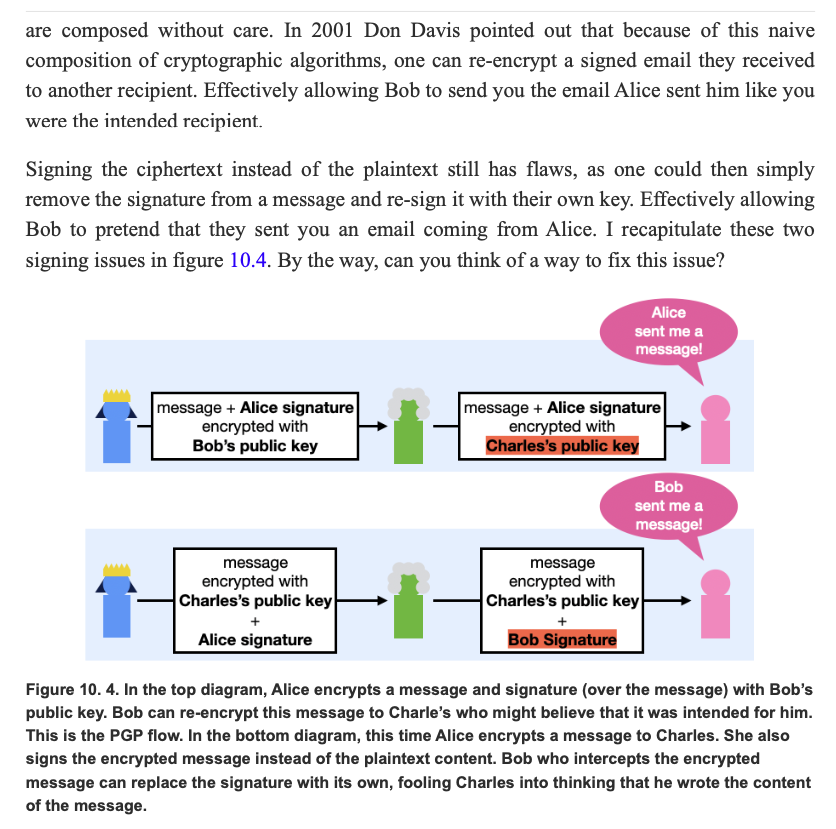
(excerpt from the book Real World Cryptography)
The latter two I don't care that much. Integration with email is doomed from my point of view. And there's just not way to have forward secrecy if we want a near-stateless system.
Email is insecure. Even with PGP, it’s default-plaintext, which means that even if you do everything right, some totally reasonable person you mail, doing totally reasonable things, will invariably CC the quoted plaintext of your encrypted message to someone else (we don’t know a PGP email user who hasn’t seen this happen). PGP email is forward-insecure. Email metadata, including the subject (which is literally message content), are always plaintext. (Thomas Ptatcek)
OK so what can I advise to my readers? What are the alternatives out there?
For file signing, Frank Denis wrote minisign which looks great.
For file encryption, I wrote eureka which does the job.
There's also magic wormhole which is often mentioned, and does some really interesting cryptography, but does not seem to address a real use-case (in my opinion) for the following reason: it's synchronous. We already have a multitude of asynchronous ways to transfer files nowadays (dropbox, google drive, email, messaging, etc.) so the problem is not there. Actually there's really no problem... we just all need to agree on one way of encrypting a file and eureka does just that in a hundred lines of code.
(There is a use-case for synchronous file transfer though, and that's when we're near by. Apple's airdrop is for that.)
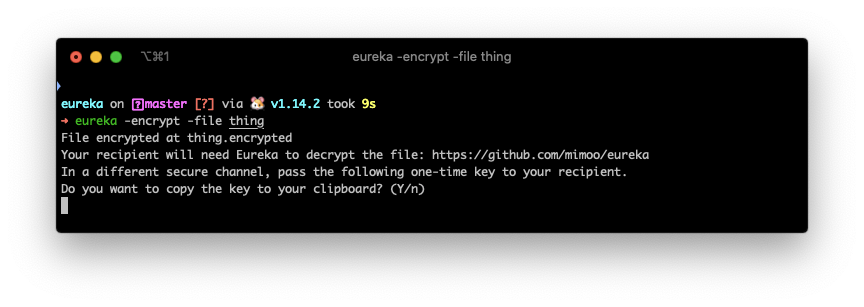
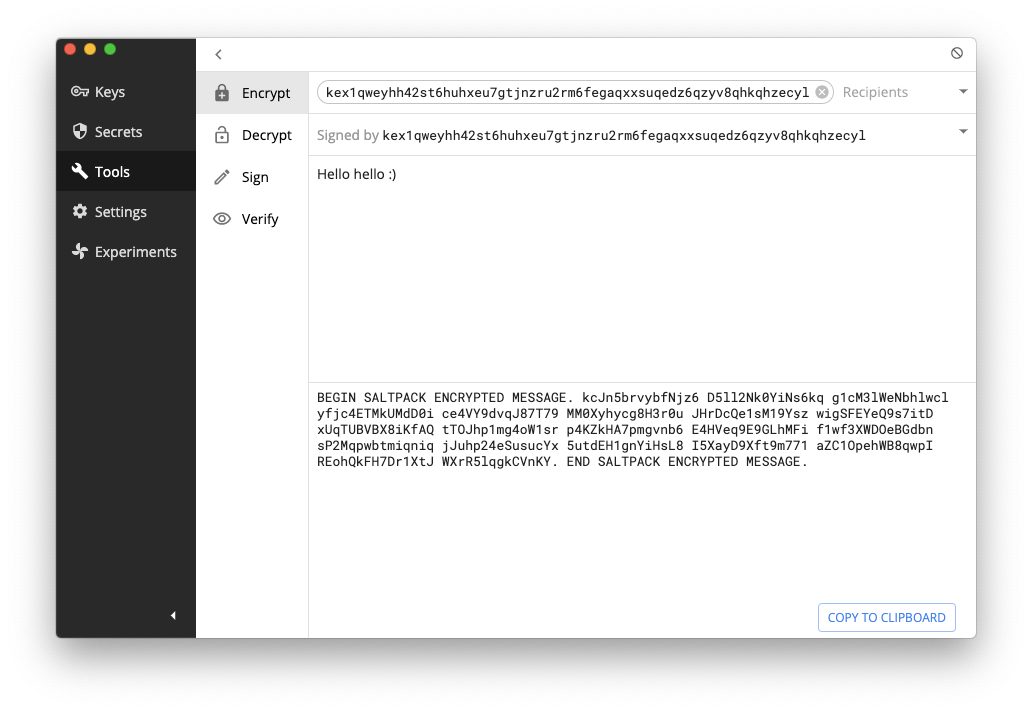
For one-time authenticated messaging (some people call that signcryption) which is pretty much the whole use-case of PGP, there seems to be only one contender so far: saltpack. The format looks pretty great and seems to address all the issues that PGP had (except for forward secrecy, but again I don't consider this a deal breaker). It seems to only have two serious implementations: keybase and keys.pub. Keybase a bit more involved, and keys.pub is dead simple and super well put.
Note that age and rage (which are excellent engineering work) seem to try to address this use case. Unfortunately they do not provide signing as Adam Caudill pointed out. Let's keep a close eye on these tools though as they might evolve in the right direction.
To obtain public keys, the web of trust (signing other people keys) hasn't been proven to really scale, instead we are now in a different key distribution model where people broadcast their public keys on various social networks in order to instill their identity to a specific public key. I don't think there's a name for it... but I like to call it broadcast of trust.
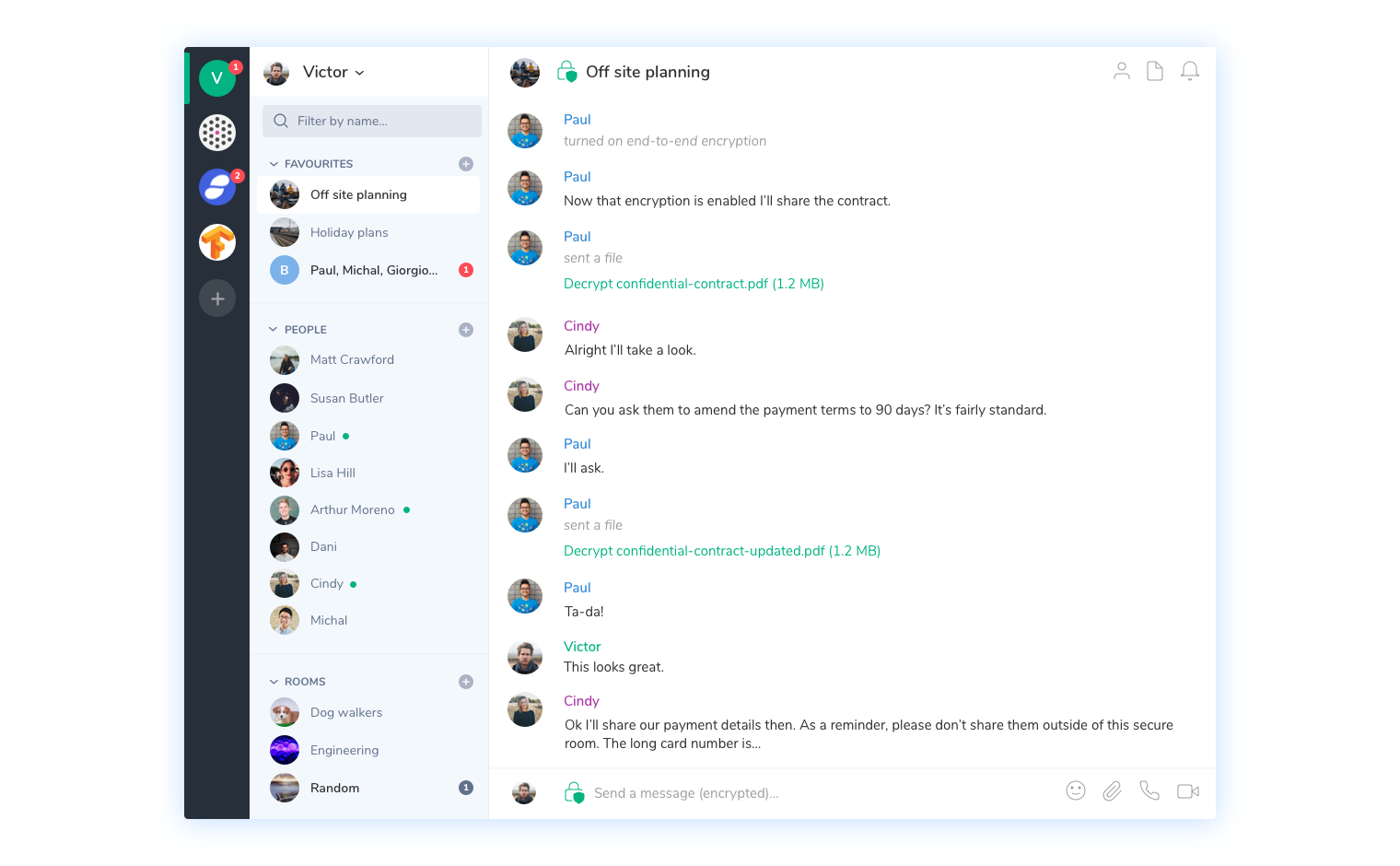
For encrypted communications, Signal has clearly succeeded as a proprietary solution, but everyone can benefit from it by using other messaging apps like WhatsApp and Wire or even federated protocols like Matrix. Matrix' main implementation seems to be Riot which I've been using and really digging so far. It also looks like the French government agrees with me.
Same thing here, the web of trust doesn't seem to work, and instead what seems to be working is relying on centralized key distribution servers and TOFU but verify (trust the first public key you see, but check the fingerprint out-of-band later).
This is end of my blog post series on cryptography with hardware.
I’ve written about smart cards and secure elements in part 1 and about HSMs and TPMs in part 2.
Trusted Execution Environment (TEE)
So far, all of the hardware solutions we’ve talked about have been standalone secure hardware solutions (with the exceptions of smart cards which can be seen as tiny computers).
Secure elements, HSMs, and TPMs can be seen as an additional computer.

(picture taken from The right secure hardware for your IoT deployment)
Let’s now talk about integrated secure hardware!
Trusted Execution Environment (TEE) is a concept that extends the instruction set of a processor to allow for programs to run in a separate secure environment. The separation between this secure environment and the ones we are used to deal with already (often called “rich” execution environment) is done via hardware. So what ends up happening is that modern CPUs run both a normal OS as well as a secure OS simultaneously. Both have their own set of registers but share most of the rest of the CPU architecture (and of course system). By using clever CPU-enforced logic, data from the secure world cannot be accessed from the normal world.
Due to TEE being implemented directly on the main processor, not only does it mean a TEE is a faster and cheaper product than a TPM or secure element, it also comes for free in a lot of modern CPUs.
TEE like all other hardware solutions has been a concept developed independently by different vendors, and then a standard trying to play catch up (by Global Platform).
The most known TEEs are Intel’s Software Guard Extensions (SGX) and ARM’s TrustZone. But there are many more like AMD PSP, RISC-V MultiZone and IBM Secure Service Container.
By design, since a TEE runs on the main CPU and can run any code given to it (in a separate environment called an “enclave”), it offers more functionality than secure elements, HSMs, TPMs (and TPM-like chips).
For this reason TEEs are used in a wilder range of applications. We see it being used in clouds when clients don’t trust servers with their own data, multi-party computation (see CCF), to run smart contracts.
TEE’s goal is to first and foremost thwart software attacks. While the claimed software security seems to be really attractive, it is in practice hard to segregate execution while on the same chip as can attest the many software attacks against SGX:
Trustzone is not much better, Quarkslab has a list of paper successfully attacking it as well.
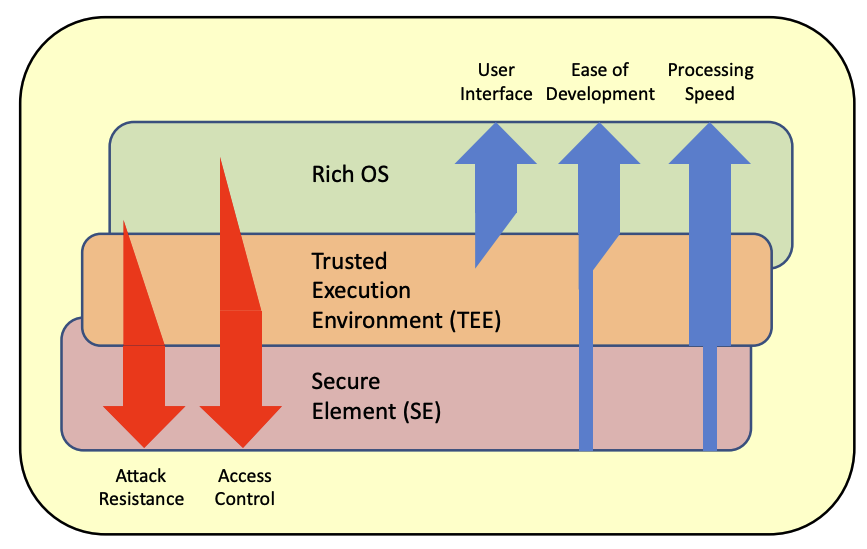
(picture taken from Certification of the Trusted Execution Environment – one step ahead for secure mobile devices)
In theory a TPM can be re-implemented in software only via a TEE (which was done by Microsoft) but one must be careful as again, TEE as a concept provides no resistance against hardware attacks besides the fact that things at this microscopic level are way too tiny and tightly packaged together to analyze without expensive equipment. But by default a TEE does not mean you’ll have a secure internal storage (you need to have a fused key that can’t be read to encrypt what you want to store), or a hardware random number generator, and other wished hardware features. But every manufacturers sure has different offers with different levels of physical security and tamper resistance when it comes to chip that supports TEE.
Hardware Security Tokens
Finally, hardware security tokens are keys that you can usually plug into your machine and that can do some cryptographic operations. For example yubikeys are small dongles that you can plug in the USB port of a laptop, and that will perform some cryptographic operations if you touch its yellow ring.

The word “token” in hardware security token comes from the fact that using it produces a “token” per-authentication request instead of sending the same credentials over and over again.
Yubikeys started as a way to provide 2nd factor authentication, usually in addition to a password, which an attacker can’t exploit in a phishing attack. The idea is that if an attacker calls your grandmother, and asks her to spell out the yubikey output, she won’t be able to. There is no output. Furthermore, modern yubikeys implement the FIDO 2 protocol which will not produce the correct response unless you are on the right webpage (if we are talking about usage for the web). The reason is that the protocol signs metadata that is linked to what’s in the url bar of your browser.
More recently laptops and mobile devices have started offering other ways to provide the same value as a hardware security token via their own secure module. For example Apple provides a biometric-protected (Touch ID or Face ID) authenticator via the secure enclave.
It’s not clear how much protection against hardware attacks your typical hardware security token has to implement since the compromise of one is not enough to authenticate as a user in most cases (unless you use one as single factor authentication). Yet yubikeys are known to have secure elements inside. Still, this doesn’t exclude software attacks if badly programmed.
For example in 2013, a low-cost and non-intrusive side-channel attack managed to extract keys from a yubikey.
Cryptocurrency has similar dongles that will sign transactions for a user, but the threat model is different and they will usually have to authenticate the user in some ways and provide tamper resistance. Here is a picture of a Nano ledger.

As with any hardware solutions, attacks have been found there as well (for example one the trezor).
Conclusion
As a summary, this 3-part blog series surveys different techniques that exist to deal with physical attacks:
- Smart cards are microcomputers that needs to be turned on by an external device like a payment terminal. They can run arbitrary java applications. Bank cards are smart cards for example.
- Secure elements are a generalization of smart cards, which rely on a set of Global Platform standards. SIM Cards are secure elements for example.
- TPMs are re-packaged secure elements plugged on personal and enterprise computers’ motherboards. They follow a standardized API (by the Trusted Computing Group) that are used in a multitude of ways from measured/secure boot with FDE to remote attestation.
- HSMs can be seen as external and big secure elements for servers. They’re faster and more flexible. Seen mostly in data centers to store keys.
- TEEs like TrustZone and SGX can be thought of secure elements implemented within the CPU. They are faster and cheaper but mostly provide resistance against software attacks unless augmented to be tamper-resistant. Most modern CPUs ship with TEEs and various level of defense against hardware attacks.
- Hardware Security Tokens are dongles like yubikeys that often repackage secure elements to provide a 2nd factor by implementing some authentication protocol (usually TOTP or FIDO2).
- There are many more that I haven’t talked about. In reality vendors can do whatever they want. We’ve seen a lot of TPM-like chips. Apple has the secure enclave, Google has Titan, Microsoft has Pluton, Atmel for example sells “crypto elements”.
Keep in mind that no hardware solution is the panacea, you're only increasing the attack's cost. Against a sophisticated attacker all of that is pretty much useless. For this reason design your system so that one device compromised doesn't imply all devices are compromised. Even against normal adversaries, compromising the main operating system often means that you can make arbitrary calls to the secure element. Design your protocol to make sure that the secure element doesn't have to trust the caller by either verifying queries, or relying on an external trusted part, or by relying on a trusted remote party, or by being self-contained, etc. And after all of that, you still have to worry about side channel attacks :)
PS: thanks to Gabe Pike for the many discussions around TEE!
In the previous post (part 1) you learned about:
- The threat today is not just an attacker intercepting messages over the wire, but an attacker stealing or tampering with the device that runs your cryptography. So called Internet of Things (IoT) devices often run into this type of threats and are by default unprotected against sophisticated attackers.
- Hardware can help protect cryptography applications in highly-adversarial environment. One of the idea is to provide a device with a tamper-resistant chip to store and perform crypto operations. That is, if the device falls in the hands of an attacker, extracting keys or modifying the behavior of the chip will be hard. But hardware-protected crypto is not a panacea, it is merely defense-in-depth, effectively slowing down and increasing the cost of an attack.
- smart cards were one of the first such secure microcontroller that could be used as a micro computer to store secrets and perform cryptographic operations with them. These are supposed to use a number of techniques to discourage physical attackers.
- the concept of a smart card was generalized as a secure element, which is a term employed differently in different domains, but boils down to a smart card that can be used as a coprocessor in a greater system that already has a main processor.
- Google having troubles dealing with the telecoms to host credit card information on SIM cards (which are secure elements), the concept of secure element in the cloud was born. In the payment space this is called host card emulation (HCE). It works simply by storing the credit card information (which is a 3DES symmetric key shared with the bank) in a secure element in the cloud, and only giving a single-use token to the user: if the phone is compromised, the attacker can only use it to pay once.
All good?
In this part 2 of our blog series you will learn about more hardware that supports cryptographic operations! These are all secure elements in concept, and are all doing sort of the same things but in different contexts. Let’s get started!
Hardware Security Module (HSM)
If you understood what a secure element was, well a hardware secure module (HSM) is pretty much a bigger secure element.
Not only the form factor of secure elements require specific ports, but they are also slow and low on memory. (Note that being low on memory is sometimes OK, as you can encrypt keys with a secure element master key, and then store the encrypted keys outside of the secure element.)
So HSM is a solution for a more portable, more efficient, more multi-purpose secure element. Like some secure elements, some HSMs can run arbitrary code as well.
HSMs are also subject to their own set of standards and security level. One of the most widely accepted standard is FIPS 140-2: Security Requirements for Cryptographic Modules, which defines security levels between 1 and 4, where level 1 HSMs do not provide any protection against physical attacks and level 4 HSMs will wipe their whole memory if they detect any intrusion!
Typically, you find an HSM as an external device with its own shelf on a rack (see the picture of a luna HSM below) plugged to an enterprise server in a data center.

(To go full circle, some of these HSMs can be administered using smart cards.)
Sometimes you can also find an HSM as a PCIe card plugged into a server’s motherboard, like the IBM Crypto Express in the picture below.

Or even as small dongles that you can plug via USB (if you don’t care about performance), see the picture of a YubiHSM below.

HSMs are highly used in some industries. Every time you enter your PIN in an ATM or a payment terminal, the PIN ends up being verified by an HSM somewhere. Whenever you connect to a website via HTTPS, the root of trust comes from a Certificate Authority (CA) that stores its private key in an HSM, and the TLS connection is possibly terminated by an HSM. You have an Android or iPhone? Chances are Google or Apple are keeping a backup of your phone safe with a fleet of HSMs. This last case is interesting because the threat model is reversed: the user does not trust the cloud with its data, and thus the cloud service provider claims that its service can’t see the user’s encrypted backup nor can access the keys used to encrypt it.
HSMs don’t really have a standard, but most of them will at least implement the Public-Key Cryptography Standard 11 (PKCS#11), one of these old standards that were started by the RSA company and that were progressively moved to the OASIS organization (2012) in order to facilitate adoption of the standards.
While PKCS#11 last version (2.40) was released in 2015, it is merely an update of a standard that originally started in 1994. For this reason it specifies a number of old cryptographic algorithms, or old ways of doing things. Nevertheless, it is good enough for many uses, and specifies an interface that allow different systems to easily interoperate with each other.
While HSMs’ real goals are to make sure nobody can extract key material from them, their security is not always shining.
A lot about the security of these hardware solutions really relies on their high price, the protection techniques used not being disclosed, and the certifications (like FIPS and Common Criteria) mostly focusing on the hardware side of things. In practice, devastating software bugs have been found and it is not always straight forward to know if the HSM you use is vulnerable to any of these vulnerabilities (Cryptosense has a good summary of known attacks against HSMs).
By the way, not only the price of one HSM is high (it can easily be dozens of thousands of dollars depending on the security level), in addition to an HSM you often have another HSM you use for testing, and another one you use for backup (in case your first HSM dies with its keys in it). It can add up!
Furthermore, I still haven’t touched on the elephant in the room with all of these solutions: while you might prevent most attackers from reaching your secret keys, you can't prevent attackers from compromising the system and making their own calls to the secure hardware module (be it a secure element or an HSM). Again, these hardware solutions are not a panacea and depending on the scenario they provide more or less defense-in-depth.
By the way, if it applies to your situation modern cryptography can offer better ways of reducing the consequences of key material compromise and mis-use. For example using multi-signatures! Check my blog post on the subject.
Trusted Platform Module (TPM)
A Trusted Platform Module (TPM) is first and foremost a standard (unlike HSMs) developed in the open by the non-profit Trusted Computing Group (TCG).
The latest version is TPM 2.0, published with the ISO/IEC (International Organization for Standardization and the International Electrotechnical Commission).
A TPM complying with the TPM 2.0 standard is a secure microcontroller that carries a hardware random number generator also called true random number generator (TRNG), secure memory for storing secrets, cryptographic operations, and the whole thing is tamper resistant.
If this description reminds you of smart cards, secure element, and HSMs well… I told you that everything we were going to be talking about in this chapter were going to be secure elements of some form. (And actually, it’s common to see TPMs implemented as repackaging of secure elements.)
You usually find a TPM directly soldered to the motherboard of many enterprise servers, laptops, and desktop computers (see picture below).

Unlike solutions that we’ve seen previously though, a TPM does not run arbitrary code. It offers a well-defined interface that a greater system can take advantage of. Due to these limitations, a TPM is usually pretty cheap (even cheap enough that some IoT devices will ship with one!).
Here is a non-exhaustive list of interesting applications that a TPM can enable:
- User authentication. Ever heard of the FBI iPhone fiasco? TPMs can be used to require a user PIN or password. In order to prevent low entropy credentials to be easily bruteforced, a TPM can rate limit or even count the number of failed attempts.
- Secure boot. Secure boot is about starting a system in a known trusted state in order to avoid tampering of the OS by malware or physical intrusion. This can be done by using a platform’s TPM and the Unified Extensible Firmware Interface (UEFI) which is the piece of code that launches an operating system. Whenever the image of a new boot loader or OS or driver is loaded, the TPM can store the associated expected hash and compare it before running the code, and failing if the hash of the image is different. If you hold a public key you can also verify that a piece of code has been signed before running it. This is a gross over-simplification of how secure boot works in practice, but the crypto is pretty straight forward.
- Full disk encryption (FDE). This allows to store the key (or encrypt the key) that encrypts all data on the device at rest. If the device has been proven to be in a known good state (via secure boot) and the user authenticates correctly, the key can be released to decrypt data. When the devices is locked or shut down, the key vanishes from memory and has to be released by the TPM again. This is a must feature if you lose, or get your device stolen.
- Remote attestation. This allows a device to authenticate itself or prove that it is running specific software. In other words, a TPM can sign a random challenge and/or metadata with a key that can be tied to a unique per-TPM key (and is signed by the TPM vendor). Every TPM comes with such a unique key (called an endorsement key) along with the vendor’s certificate authority signature on the public key part. For example, during employee onboarding a company can add a new employee’s laptop’s TPM endorsement key to a whitelist of approved devices. Later, if the user wants to access one of the company’s service, the service can request the TPM to sign a random challenge along with hashes of what OS was booted to authenticate the user and prove the well-being of the user’s device.
There are more functionalities that a TPM can enable (there's afterall hundreds of commands that a TPM implements) which might even benefit user applications (which should be able to call the TPM).
Note that having a standard is great for inter-operability, and for us to understand what is going on, but unfortunately not everyone use TPMs. Apple has the secure enclave, Microsoft has Pluton, Google has Titan.
Perhaps, on a darker note, it is good to note that TPMs have their own controversies and have also been subjected to devastating vulnerabilities. For example the ROCA attack found that an estimated million TPMs (and even smart cards) from the popular Infineon vendor had been wrongly generating RSA private keys for years (the prime generation was flawed).
To recap, you’ve learned about:
- HSMs. They are external, bigger and faster secure elements. They do not follow any standard interface, but usually implement the PKCS#11 standard for cryptographic operations. HSMs can be certified with different levels of security via some NIST standard (FIPS 140-2).
- TPMs. They are chips that follow the TPM standard, more specifically they are a type of secure element with a specified interface. A TPM is usually a secure chip directly linked to the motherboard and perhaps implemented using a secure element. While it does not allow to run arbitrary programs like some secure elements, smart cards, and HSMs do, it enables a number of interesting applications for devices as well as user applications.
That’s it for now, check this blog again to read part 3 which will be about TEEs!
Many thanks to Jeremy O'Donoghue, Thomas Duboucher, Charles Guillemet, and Ryan Sleevi who provided help and reviews!
If at some point you realize that doing cryptography means having to manage long-term keys, it means you’re standing in the world of key management.
Makes sense right?
In these lands, you are going to run into scenarios where attackers can be quite close to your applications.
I call these highly-adversarial environments.
Imagine using your credit card on an ATM skimmer (a doodads that a thief can place on top of the card reader of an ATM in order to copy the content of your credit card, see picture bellow); downloading an application on your mobile phone that compromises the OS; hosting a web application in a colocated server shared with a malicious customer; managing highly-sensitive secrets in a data center that gets breached; and so on.

These scenarios suck, and are very counterintuitive to most cryptographers. This is because cryptography has come a long way since the historical “Alice wants to encrypt a message to Bob without Eve intercepting it”. Nowadays, it’s often more like “Alice wants to encrypt a message to Bob, but Alice is also Eve”.
The key here is that in these scenarios, there’s not much that can be done cryptographically (unless you believe in whitebox crypto) and hardware can go a long way to help.
OK, so now we have a whole world of new doohickeys to learn about, and there’s a lot of thingamabob believe me (hence the dense title).
It can be quite confusing to learn about all of this, so here we go: my promise is that by the end of this blogpost series you’ll have a better understanding of what are all these different hardware solutions.
Keep in mind that none of these solutions are pure cryptographic solutions: they are all defense-in-depth (and sometimes dubious) solutions that serve to hide secrets and their associated sensitive cryptographic operations. They also all have a given cost, meaning that if a sophisticated attacker decides to break the bank, there’s not much we can do (besides raising the cost of an attack).
OK let's get started.
Obfuscation
By definition obfuscation has nothing to do with security: it is the act of scrambling something so that it still work but is hard to understand. So for the laugh, let’s first mention whitebox cryptography which attempts to “cryptographically” obfuscate the key inside of an algorithm. That’s right, you have the source code of some AES-based encryption algorithm with a fixed key, and it encrypts and decrypts fine, but the key is mixed so well with the implementation that it is too confusing for anyone to extract the key from the algorithm. That's the theory. Unfortunately in practice, no published whitebox crypto algorithm has been found to be secure, and most commercial solutions are closed-source due to this fact (security through obscurity kinda works in the real world). Again, it’s all about raising the cost and making it harder for attackers.
All in all, whitebox crypto is a big industry that sells dubious products to businesses in need of DRM solutions. On the more serious side, there is a branch of cryptography called Indistinguishability obfuscation (iO) that attempts to do this cryptographically (so for realz). iO is a very theoretical, impractical, and so far not-really-proven field of research. We’ll see how that one goes.
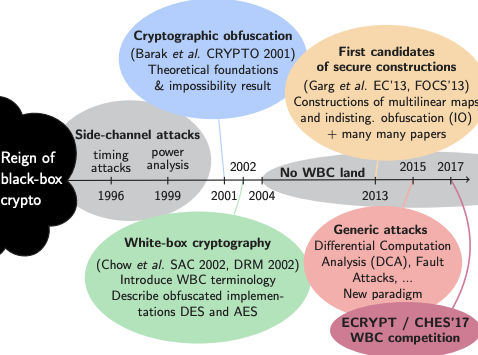
(Timeline of whitebox cryptography, taken from Matthieu Rivain’s slides)
Smart Cards
OK, whitebox crypto is not great, and worse: even if you can’t extract the key, you can still copy the program instead of trying to extract the key (and use it to do whatever cryptographic operation it features). It would be great if we could prevent people from copying secrets from sensitive devices though, or even prevent them from seeing what’s going on when the device performs cryptographic operations.
A smart card is exactly this. It’s what you commonly find in credit cards, and is activated by either inserting it into, or using Near-field Communication (NFC) by getting the smart card close enough to, a payment terminal (also called Point of Sale or PoS terminal).
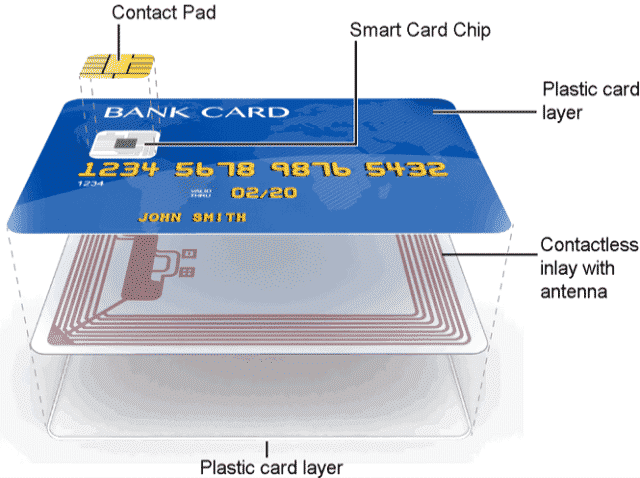
Smart cards are pretty old, and started as a practical way to get everyone a pocket computer. Indeed, a smart cart embarks a CPU, memory (RAM, ROM and EEPROM), input/output, hardware random number generator (so called TRNGs), etc.) unlike the not-so-smart cards that only had data stored in them via a magnetic stripe (which in turn can be easily copied via the skimmers I talked about previously).
Today, it seems like the same people all have a much more powerful computer in their pockets, so smart cards are probably going to die.
(Rob Wood is pointing to me that more than a quarter of the US still doesn’t have a smart phone, so there’s still some time before this prophecy come to fruition.)
Smart cards mix a number of physical and logical techniques to prevent observation, extraction, and modification of its execution environment and some of its memory (where secrets are stored). But as I said earlier, it’s all about how much money you want an attacker to be spending, and there exist many techniques that attempt at breaking these cards:
- Non-invasive attacks such as differential power analysis (DPA) analyze the power consumption of the smart card while it is doing cryptographic operations in order to extract the associated keys.
- Semi-invasive attacks require access to the chip’s surface to mount attacks such as differential fault analysis (DFA) which use heat, lasers, and other techniques to modify the execution of a program running on the smart card in order to leak the key via cryptographic attacks (see my post on RSA signature fault attacks for an example).
- Finally invasive silicon attacks can modify the circuitry in the silicon itself to alter its function and reveal secrets.
Secure Elements
Smart cards got really popular really fast, and it became obvious that having such a secure blackbox in other devices could be useful. The concept of a secure element was born: a tamper-resistant microcontroller that can be found in a pluggable form factor like UUICs (SIM cards required by carriers to access their 3G/4G/5G network) or directly bonded on chips and motherboards like the embedded SE (eSE) attached to an iPhone’s NFC chip. Really just a small separate piece of hardware meant to protect your secrets and their usage in cryptographic operations.
SEs are an evolution of the traditional chip that resides in smart cards, which have been adapted to suit the needs of an increasingly digitalized world, such as smartphones, tablets, set top boxes, wearables, connected cars, and other internet of things (IoT) devices. (GlobalPlatform)
Secure elements are a key concept to protect cryptographic operations in the Internet of Things (IoTs), a colloquial (and overloaded) term to refer to devices that can communicate with other devices (think smart cards in credit cards, SIM cards in phones, biometric data in passports, garage keys, smart home sensors, and so on).
Thus, you can see all of the solutions that will follow in this blogpost series as secure elements implemented in different form factors, using different techniques, and providing different level of defense-in-depth.
If you are required to use a secure element (to store credit card data for example), you also most likely have to get it certified. The main definition and standards around a secure element come from GlobalPlatform, but there exist more standards like Common Criteria (CC), NIST’s FIPS, EMV (for Europay, Mastercard, and Visa), and so on.
If you’re in the market of buying secure microcontrollers, you will often see claims like “FIPS 140-2 certified” and “certified CC EAL 5+” next to it. Claims that can be obtained after spending some quality time, and a lot of money, with licensed certification labs.
Host Card Emulation (HCE)
It’s 2020, most people have a computer in their pocket: a smart phone. What’s the point of a credit card anymore? Well, not much, nowadays more and more payment terminals support contactless payment via the Near-field Communication (NFC) protocol, and more and more smartphones ship with an NFC chip that can potentially act as a credit card.
NFC for payment is specified as Card Emulation. Literally: it emulates a bank card.
Banks allow you to do this only if you have a secure element.
Since Apple has full control over its hardware, it can easily add a secure element to its new iPhones to support payment, and this is what Apple did (with an embedded SE bonded to the NFC chip since the iPhone 6). iPhone users can register a bank card with the Apple wallet application, Apple can then obtain the card’s secrets from the issuing bank, and the card secrets can finally be stored in the eSE. The secure element communicates directly with the NFC chip and then to NFC readers, thus a compromise of the phone OS does not impact the secure element.
Google, on the other hand, had quite a hard time introducing payment to Android-based mobile phones due to phone vendors all doing different things. The saving technology for Google ended up being a cloud-based secure element called Host Card Emulation (HCE) introduced in 2013 in Android 4.4.
How does it work? Google stores your credit card information in a secure element in the cloud (instead of your phone), and only gives your phone access to short-lived single-use PAN (card numbers).
(Note that some Android devices do have an eSE that can be used instead of HCE, and some SIM cards can also be used as secure elements for payment.)
This concept of replacing sensitive long-term information with short-lived tokens is called tokenization.
Sending a random card number that can be linked to your real one is great for privacy: merchants can’t track you as it’ll look like you’re always using a new card number. If your phone gets compromised, the attacker only gets access to a short-lived secret that can only be used for a single payment.
Tokenization is a common concept in security: replace the sensitive data with some random stuff, and have a table secured somewhere safe that maps the random stuff to the real data.
Wikipedia has some cool diagram to show what’s going on whenever you pay with Android Pay or Apple Pay:
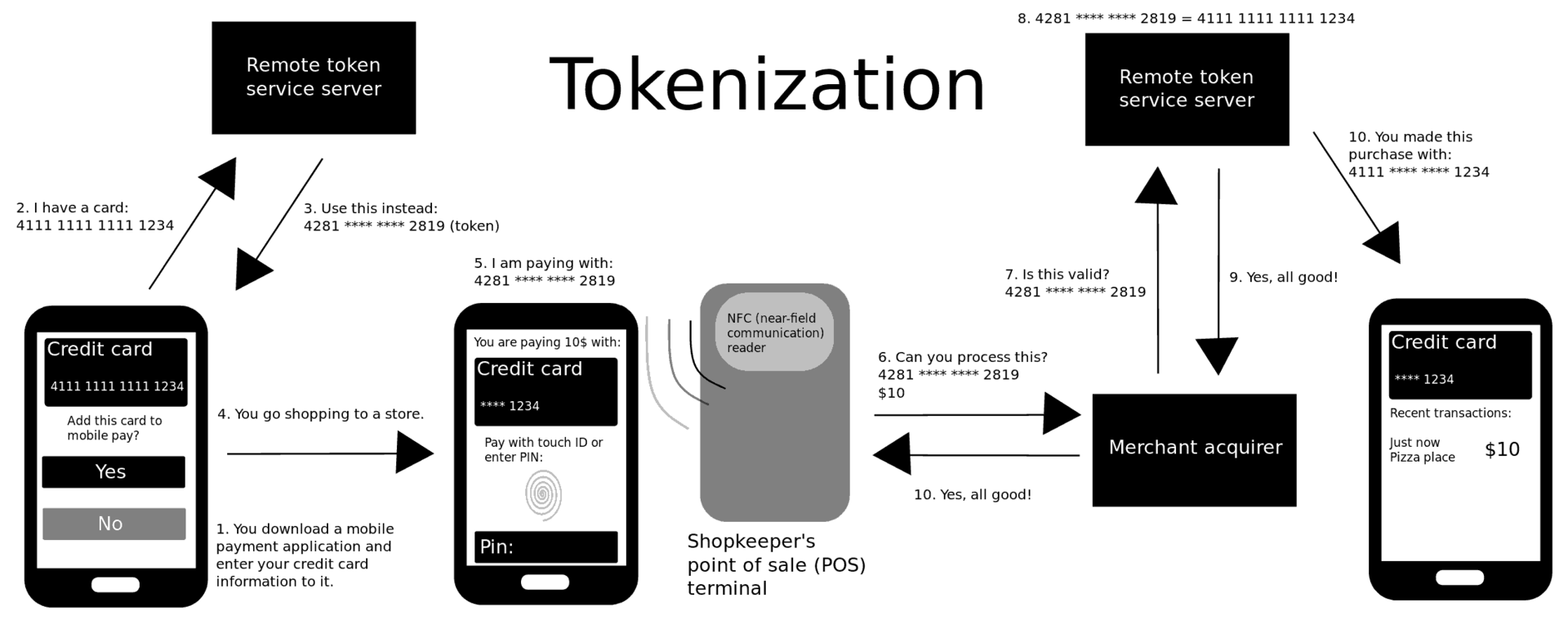
Although Apple theoretically doesn't have to use tokenization, since iPhones have secure elements that can store the real PAN, they do use it in order to gain more privacy (it's afterall their new bread and butter).
In part 2 of this blog series I’ll cover HSMs, TPMs, and much more :)
(I would like to thank Rob Wood, Thomas Duboucher, and Lionel Rivière for answering my many questions!)
PS: I'm writing a book which will contain this and much more, check it out!
The coronavirus is shaking the world, on its multiple layers, and cryptography hasn't been spared.
The IACR announced on March 14th that multiple conferences were postponed:
FSE 2020, which was supposed to be held in Athens, Greece, during 22-26 March 2020, has been postponed to 8-12 November 2020.
PKC 2020, which was supposed to be held in Edinburgh, Scotland, during 4-7 May 2020, has been postponed.
EUROCRYPT 2020, which was supposed to be held in Zagreb, Croatia, during 10-14 May 2020, has been postponed.
While some others were not:
No changes have been made at this time to the schedule of CRYPTO 2020, CHES 2020, TCC 2020, and ASIACRYPT 2020, but we will continue to closely monitor the situation and will inform members if changes are needed.
While many workplaces (including mine) are moving to a WFH (work from home) model, will conferences follow?
It seems to be the case at least for Consensus 2020, a cryptocurrency conference organized by coindesk, which is moving to an online model:
Consensus 2020 will now be a completely virtual experience, where attendees from all over the world can participate online at no charge.
On a more dramatic note it seems like several participants of EthCC, which was held in Paris almost a week ago, have contracted the virus. A google spreadsheet has been circulating in order to self-report and figure out who else could have potentially contracted the virus.
Even Vitalik Buterin is rumored to have had mild COVID-19 symptoms. Nobody is out of reach.
On a lighter note, my coworker Kostas presented on proofs of solvency at the lightning talks of Real World Crypto 2020. With his merkle tree-like construction he hopes to make governments accountable when they count the number of people who counted positive to the virus.






























