Quick access to articles on this page:
more on the next page...

At 2am this morning Libra was released.
and it seems to have broken the internet (sorry about that ^.^")
I've never worked on something this big, and I'm overwhelmed by all this reception. This is honestly pretty surreal from where I'm standing.
Libra is a cryptocurrency, which is on-par with other state-of-the-art blockchains. Meaning that it attempts to solve a lot of the problems Bitcoin originally had:
- Energy Waste. The biggest reproach that people have on Bitcoin, is that it wastes a lot of our electricity. Indeed, because of the proof of work mechanism people constantly use machines to hash useless data in order to find new blocks. Newer cryptocurrencies, including Libra, make use of Byzantine Fault Tolerance (BFT) consensus protocols, which are pretty green by definition.
- Efficiency. Bitcoin is notably slow, with a block being mined every 10 minutes, and a minimum confirmation time of one hour. BFT allows us to "mine" a new block every 3 seconds (in reality it can even go much faster).
- Safety. Another problem with Bitcoin (or proof of work-based cryptocurrencies) is that it forks, constantly, and then re-organize itself around the "main chain". This is why one must wait several blocks to confirm that their transaction has been included. This concept is not great at all, as we've seen with Ethereum Classic which was forked (not so long ago) with more than 100 block in the past! BFT protocols never fork once they commit a block. What you see on the chain, is the final chain always. This is why it is so fast (and so sexy).
- Stability. This one is pretty self-explanatory. Bitcoin's price has been anything but stable. Gamblers actually strive on that. But for a global currency to be useful, it has to keep a certain rate for people to use it safely. Libra uses a reserve of real assets to back the currency. This is the most conservative way to achieve stability, and it is probably the most contentious point about Libra, but one needs to remember that this is all in order to achieve stability. Stability is required if we want this to be useful for everyone.
- Adoption. This final point is the most important in my opinion, and this is the reason I've joined Facebook on this journey. Adoption is the largest problem to all cryptocurrencies right now, even though you hear about them in the news very few people use them to actually transact (and most people use them to speculate instead). The mere size of the association (which is planned to reach 100 members from all around the world) and the user-base of Facebook is going to be a big factor in adoption. That's the most exciting thing about the project.
On top of that, it is probably one of the most interesting projects in cryptography right now. The codebase is in Rust, it uses the Noise Protocol Framework, it will include BLS signatures and formally verified smart contracts. And there's a bunch of other exciting stuff to discover!
If you're interested you should definitely check the many papers we've published:
I've read many comments about this project, and here's how I would summarize my point of view: this is a crazy and world-scale project. There are not many projects with such an impact, and we'll have to be very careful about how we walk towards that goal. How will it change the world? Like a lot of global projects, it will have its ups and downs, but I believe that this is a positive net worth project for the world (if it works). We're in a unique position to change the status quo for the better. It's going to be exciting :)
If you're having trouble understanding why this could work, think about it this way. You currently can't transact money easily as soon as you're crossing a border, and actually, for a lot of countries (like the US) even intra-border money transfers are a pain. Currently the best banks in the world are probably Monzo and Revolut, and they're not available everywhere. Why? Because the banking system is very complex. By using a cryptocurrency, you are skipping decades of progress and setting up a interoperable network. Any banks and custody wallets can now use this network. You literally get the same thing you would get with your normal bank (same privacy, same usability, etc.) except that now banks themselves have access to a cheap and global network. The cherry on top is that normal users can bypass banks and use it directly, and you can monitor the total amount of money on the network. No more random printing of money.
A friend compared this project to nuclear energy: you can debate about it long and large, but there's no doubt it has advanced humanity. I feel the same way about this one. This is a clear improvement.
I've started writing a book on applied cryptography at the beginning of 2019, and I will soon release a pre-access version. I will talk about that soon on this blog!

(picture taken from the book)
The book's audience is for students, developers, product managers, engineers, security consultants, curious people, etc. It tries to avoid the history of cryptography (which seems to be unavoidable in any book about cryptography these days), and shy away from mathematical formulas. Instead, it relies heavily on diagrams! A lot of them! As such, it is a broad introduction to what is useful in cryptography and how one can use the different primitives if seen as black boxes. It attempts to also serve the right amount of details, to satisfy the reader's curiosity. I'm hopping for it to be a good book for quickly getting introduced to different concepts going from TLS to PAKE. It will also include more modern topics like post-quantum cryptography and cryptocurrencies.
I don't think there's anything like this yet. the classic Applied Cryptography is quite old now and did not do much to encourage best practices or discourage rolling your own. The excellent Serious Cryptography is more technical and has more depth than what I'm aiming for. My book will rather be something in between, or something that would (hopefully) look like Matthew Green's blog if it was a book (minus a lot of the humor, because I suck at making jokes).
More to come!
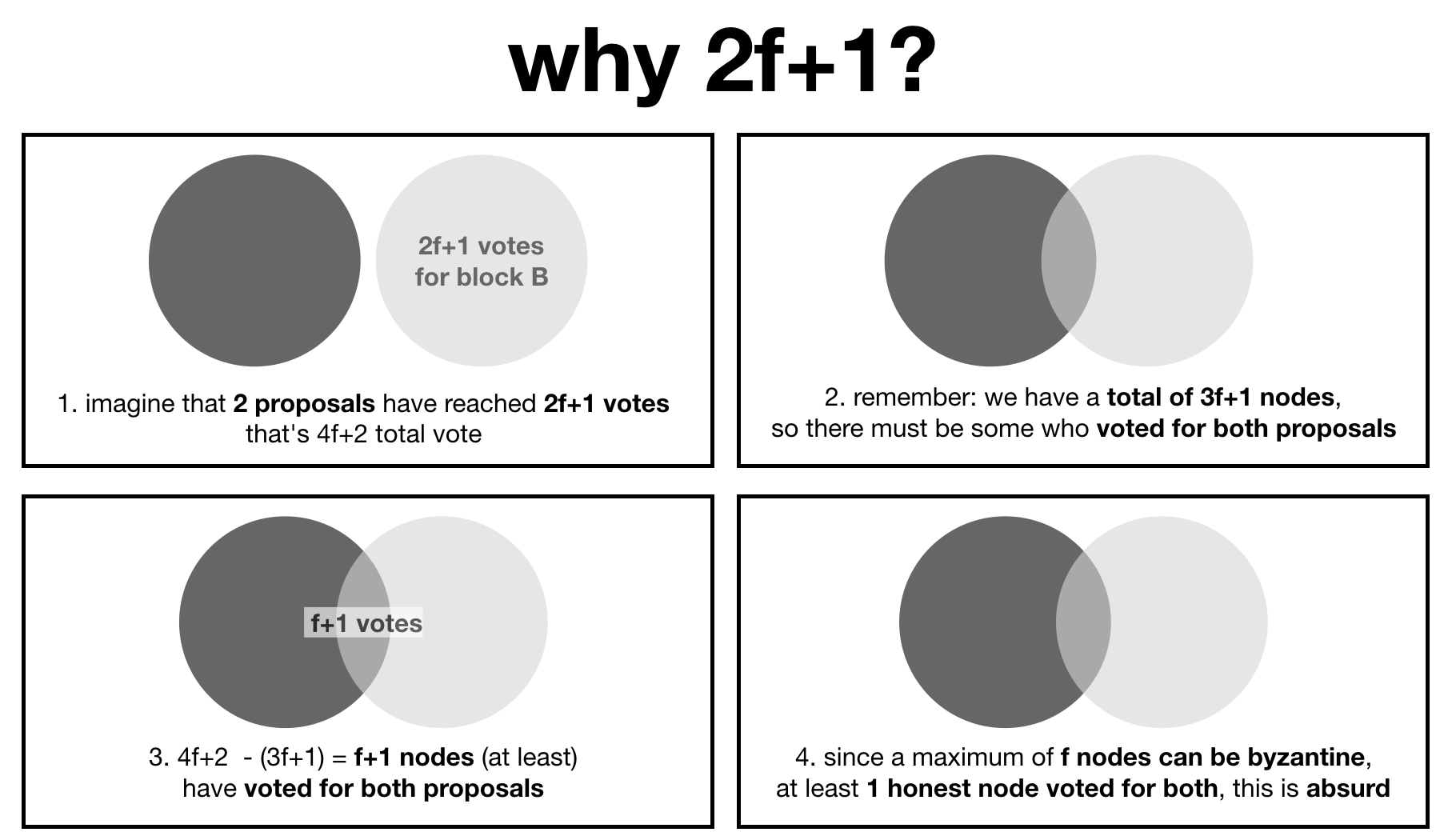
Have you ever wondered why byzantine agreement protocols seem to all start with the assumptions that less than a third of the participants can be malicious?
This axiom is useful down the line when you want to prove safety, or in other words that your protocol can't fork. I made a diagram to show that, an instance of the protocol that forks (2 proposals have been committed with 2f+1 votes from the participants) is absurd.
As I'm transitioning to the Blockchain team of Facebook, I decided it would be a good time to give this place a bit of a refresh :)
I've started blogging here in 2013:
I quickly found out a layout I liked and sticked with it. In 2014 it looked like this:
In 2018 it looked a bit different:

And finally the new re-design which should be brighter:
Hope you like it :)
I already wrote a lot about Disco:
Today, I released the white paper that introduces the construction. Check it out on ePrint.

It's a combination of everything I've talked about, plus:
- some experimental results on embedded devices done by Matteo Bocchi and Ruggero Susella
- some preliminary results on formal verification with Tamarin Prover
I unfortunately did not have the time to complete the formal verification of several important lemmas. But I am hopping that I can achieve this in a later paper. The formal verification code is on github and anybody is welcome to help :)
1. Bits and Their Encoding
Imagine that I generate a key to encrypt with AES. I use AES-128, instead of AES-256, so I need a 128-bit key.
I use whatever mechanism my OS gives me to generate a long string of bits. For example in python:
>>> import os;
>>> random_number = os.urandom(16)
>>> print(bin(int(random_number, 16))[2:])
11111010110001111100010010101111110101101111111011100001110000001000010100001000000010001001000110111000000111101101000000101011
These bits, can be interpreted as a large number in base 2. Exactly how you would interpret 18 as "eighteen" in base 10.
This is the large number in base 10:
>>> print(int(random_number, 16))
333344255304826079991460895939740225579
According to wolframalpha it reads like so in english:
333 undecillion 344 decillion 255 nonillion 304 octillion 826 septillion 79 sextillion 991 quintillion 460 quadrillion 895 trillion 939 billion 740 million 225 thousand 579.
This number can be quite large sometimes, and we can make use of letters to shorten it into something more human readable. Let's try base 16 which is hexadecimal:
>>> print(random_number.encode('hex'))
fac7c4afd6fee1c085080891b81ed02b
You often see this method of displaying binary strings to a more human readable format. Another popular one is base64 which is using, you guessed it, base 64:
>>> import base64
>>> print(base64.b64encode(random_number))
+sfEr9b+4cCFCAiRuB7QKw==
And as you can see, the bigger the base, the shorter the string we get. That is quite useful to keep something human readable and short.
2. Bytes and Bit-wise Operations
Let's go back to our bitstring
11111010110001111100010010101111110101101111111011100001110000001000010100001000000010001001000110111000000111101101000000101011
this is quite a lot of bits, and we need to find a way to store that in our computer memory.
The most common way, is to pack these bits into bytes of 8 bits (also called one octet):
11111010 11000111 11000100 10101111 11010110 11111110 11100001 11000000 10000101 00001000 00001000 10010001 10111000 00011110 11010000 00101011
As you can see, we just split things every 8 bits. In each bundle of 8 bits, we keep the bit-numbering with the most significant bit (MSB) first. We could have had the least significant bit (LSB) first instead, but since our larger binary string already had MSB first, it makes sense to keep it this way. It's also more "human" as we are used to read numbers from left to right (at least in English, French, Chinese, etc.)
Most programming languages let you access octets instead of bits directly. For example in Golang:
a := []byte{98, 99} // an array of bytes
b := a[0] // the byte represented by the base 10 number '98'
To act on a specific bit, it's a bit more effort as we need to segregate it via bitwise operations like NOT, AND, OR, XOR, SHIFTs, ROTATIONs, etc.
For example in Golang:
a := byte(98)
firstBit := a >> 7 // shifting 7 bits to the right, leaving the MSB intact and zero'ing the others
So far, all of these things can be learned and anchored in your brain by writing code for something like cryptopals for example.
3. Memory
OK. How do we store these octets in memory? Unfortunately, because of historical reasons, we have two ways of doing this:
- Big-Endian: from low memory address (00000....) to high memory address (999999...) in that order.
- Little-Endian: from high memory address (9999999...) to lower memory address (0000000...) in that order.
We call this Endianness.
I'm sorry, but to understand the rest of this article, you are going to have to parse this small snippet of C first:
#include <stdlib.h>
#include <stdio.h>
#include <stdint.h>
int main(){
uint8_t a[] = {1, 255}; // storing [1, 255]
printf("%p: x\n", a, *a); // 0x7ffdc5e78a70: 01
printf("%p: x\n", a+1, *(a+1)); // 0x7ffdc5e78a71: ff
}
As we can see, everything works as expected:
a points to an address in memory (0x7ffdc5e78a70) containing $1$- the next address (
0x7ffdc5e78a71) points to the value $255$ (displayed in hexadecimal)
The number 0x01ff (the 0x is a nice way to indicate that it is hexadecimal) represents the number $1 \times 16^2 + 15 \times 16^1 + 15 \times 16^0 = 511$ (remember, f represents the number 15 in hexadecimal).
So let's try to store that number in a different way in C:
#include <stdlib.h>
#include <stdio.h>
#include <stdint.h>
int main(){
uint16_t b = 0x01ff; // storing [1, 255] ?
//uint16_t b = 511 // these two lines are equivalent
uint8_t *a = (uint8_t*)&b; // getting octet pointer on b
printf("%p: x\n", a, *a); // 0x7ffd78106986: ff
printf("%p: x\n", a+1, *(a+1)); // 0x7ffd78106987: 01
}
Wait what? Why is the order of 01 and ff reversed?
This is because the machine I used to run this uses little-endianness to map values to memory (like most machines nowadays).
If you didn't know about this, it should freak you out.
But relax, this weirdness almost NEVER matters. Because:
- in most languages, you do not do pointer arithmetic (what I just did when I incremented
a)
- in most scenarios, you do not convert back and forth between bytestrings and number types (like
int or uint16_t).
And this is pretty much why most systems don't care too much about using little-endian instead of big-endian.
4. Network
Networking is usually the first challenge someone unfamiliar with endianness encounters.
When receiving bytes from a TCP socket, one usually stores them into an array. Here is a simple example in C where we receive a string from the network:
char *a = readFromNetwork() // [104, 101, 108, 108, 111, 0]
printf("%s\n", a); // hello
Notice that we do not necessarily know in which order (endianness) the bytes were sent, but protocols usually agree to use network byte order which is big-endian. This works pretty well for strings, but when it comes to number larger than 8-bit, you need to know how to re-assemble it in memory depending on your machine.
Let's see why this is a problem. Imagine that we want to transmit the number $511$. We need two bytes: 0x01 and 0x0ff. We transmit them in this order since it is big-endian which is the prefered network-byte order. On the other side, here is how we can receive the two bytes, and convert them back into a number type:
uint8_t a1[] = {1, 255}; // storing the received octets as-is (from left to right)
uint8_t a2[] = {255, 1}; // storing the octets from right to left after reversing them
uint16_t *b1 = (uint16_t*)a1;
uint16_t *b2 = (uint16_t*)a2;
printf("%"PRIu16"\n", *b1); // 65281
printf("%"PRIu16"\n", *b2); // 511
In this case, we see that to collect the correct number $511$ on the other end of the connection, we had to reverse the order of the bytes in memory. This is because our machine is little-endian.
This is what confuses most people!
In reality, it shouldn't. And this should re-assure you, because trying to figure out the endianness of your machine before converting a series of bytes received from the network into a number can be daunting.
Instead, we can rely on bitwise operations that are always emulating big-endianness! Let's take a deep look at this short snippet of code:
uint8_t* a[] = {1, 255}; // the number 511 encoded in network byte-order
uint16_t b = (a[0] << 8) | a[1];
printf("%"PRIu16"\n", b); // 511
Here, we placed the received big-endian numbers in the correct big-endian order via the left shift operation. This code works on any machine. It is the key to understanding why endianness doesn't matter in most cases: bit-wise operations are endianness-independent.
Unless your job is to implement low-level stuff like cryptogaphy, you do not care about endianness. This is because you will almost never convert a series of bytes to a number, or a number to a series of bytes.
If you do, because of networking perhaps, you use the built-in functions of the language (see Golang or C for example) and endianness-independent operations (like left shift), but never pointer arithmetic.
MIT Computer Science & Artificial Intelligence Lab just released some new research. The paper is called Vault: Fast Bootstrapping for Cryptocurrencies.
From a high level, it looks like a new cryptocurrency. But it is written as a set of techniques to improve Algorand and other cryptocurrencies are encouraged to adopt them, which leads me to think this will probably not become another cryptocurrency. It is very well written and I thought I would write a summary here.
After installing a cryptocurrency client, you usually sync it with the network in order to be able to participate or see the latest state of the blockchain. This whole concept of joining a cryptocurrency as a client is costly. For example, to join Bitcoin you need to download the whole blockchain which is more than 150 GB at the moment. It can take days and lot of bandwidth.
The whole point of Vault (the paper) is about reducing this bootstrapping process, and the space needed after to keep using the blockchain. It includes three techniques which I will briefly summarize below:
First technique: balance pruning.
Ethereum got rid of Bitcoin's UTXOs and keeps track of all the account balances instead. This method already saves a lot of space. Once you do that though, you are required to keep track of a nonce per account. This is to prevent transactions replay.
How does the Ethereum nonce works: when you sign a transaction, you also sign the nonce. Once it gets accepted in a block the nonce of your account gets incremented, and the next transaction will need to sign the new nonce to get accepted.
Vault doesn't keep a nonce, instead it tracks the hashes of all the transactions that were applied. This way, If you try to replay a transaction, it will be detected.
That's too costly though, we don't want to store ALL of the transactions ever. So the first technique is to force transactions to expire. Once a transaction is expired, a client can get rid of it in its storage, as it cannot be replayed (it is not valid anymore).
Another issue with Ethereum are zero-balance accounts.
Our analysis of the Ethereum state indicates that around 38% of all accounts have no funds and no storage/contract data (i.e., only an address and a nonce)
These zero-balance accounts still need to be tracked because of the nonce that is still useful to prevent future transaction replays.
In Vault, once all transactions applied on a zero-balance account have expired, you can prune the account.
This first technique allows a lot of useless data to be cleaned out. A client only stores accounts that have a balance greater than zero, zero-balance accounts if they still have transactions that could be replayed, and recent committed/pending transactions that haven't expired yet.
Second technique: balance sharding.
Keeping track of all the accounts is costly for one client... We can do better.
Vault uses a sparse Merkle tree where the leaves represent all the possible accounts.
It's quite a large tree... so we can split it in shards! The first $X$ bits of someone's public key could indicate what shard they should store. For example if we want to have 4 shards, the first 2 bits would indicate the path in the tree (0 is left, 1 is right).
Instead of storing all the leaves, you would store all the leaves that belong to your "subroot" (specified by the first bits of your public key).
By doing this we can't verify transactions anymore though...
To solve this, every transaction now ships with a proof of membership (a witness) for both the sender and recipient addresses.
This proof of membership is a typical merkle tree concept, it contains the neighbor nodes of the leaf's path up to the root as well as the leaf itself (account balance). This way anyone can verify a transaction!
Furthermore, once a transaction is committed to a block, the merkle tree is updated and its root are updated as well (because an account balance (a leaf) has changed).
So pending transactions in the mempool (the pool of pending transactions) need to have their membership proofs updated. Anybody has enough information to do this so it is not a problem. (By the way this is why transactions carry the recipient address' witness (the membership proof)l: because that leaf gets affected by a transaction as well.)
These two proofs are quite long though, and they accompany every transactions being broadcasted on the network!
One way to reduce that is to decrease the length of the membership proof. To do this, every client stores a level of subroots of the balance merkle tree, this way a proof doesn't need to go up to the root, but up to the level that the client has stored. The rest can be calculated from what is on disk.
Thanks to this second technique, one only needs to keep track of his own leaf (account balance) as well as the balance merkle root. And one can still verify new blocks. If one wants to help storing part of the network, one can keep track of a shard instead of the whole list of accounts.
I think the sharding thing here is actually less important than the transactions shipping with the balance proofs. But it is still a neat way of making sure that all nodes can participate in conserving the full blockchain and its balances.
Third technique: stamping certificates.
Vault is built on top of Algorand. The Algorand protocol is so elegant, I can see why they would want to make use of it.
Algorand's byzantime agreement BA* produces a "certificate" for each block committed to the blockchain. A certificate is a bundle containing more than 2/3rd signatures of the block from a randomly selected committee. Such a certificate is quite large (lots of signatures, public keys, and proof that the public key could participate in BA*). In addition, Algorand "mines" a new block every 2-3 seconds, so it has quite a large blockchain and a new client needs to download and verify a huge number of blocks to join the network.
To speed this up, Vault has nodes create additional "stamped certificates" at larger intervals (one every thousand blocks or so). From one stamped certificate, you can fast forward thousands of blocks ahead (~2 days of history) to the next stamped certificate. To create these stamped certificates, they use the same cryptographic sortition technique that Algorand uses but with a smaller number of participants to reduce the size of the stamped cert. (No, BLS and aggregate signatures won't help because as I've said a certificate contains a lot of distinct objects).
This way, to join the network, a client can validate blocks and certificates until it finds its first stamped certificate, then the client can jump thousands of blocks ahead from stamped certificate to stamped certificate until it reaches the most up-to-date block. There are more optimizations and details to it addressed in the paper.
I the end these stamped certificates are some kind of checkpoints. I find that it is not as elegant as Coda's protocol solution which only contains one zero-knowledge proof of the whole chain, but ZK-SNARKS being quite complicated I can see how one would want to avoid them.

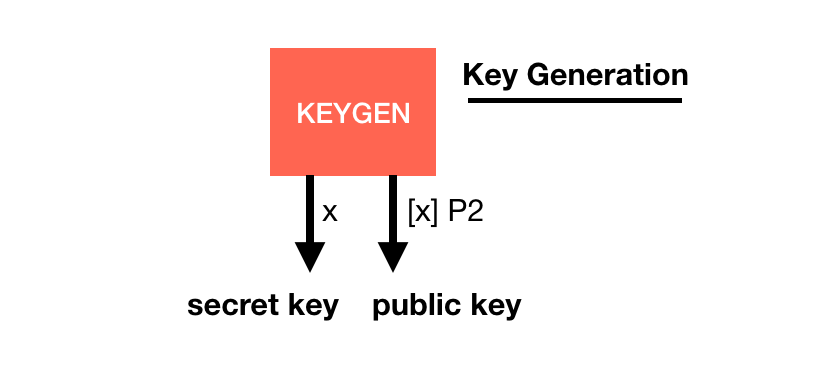
BLS is a digital signature scheme being standardized.
Its basis is quite similar to other signature schemes, it has a key generation with a generator $P2$:
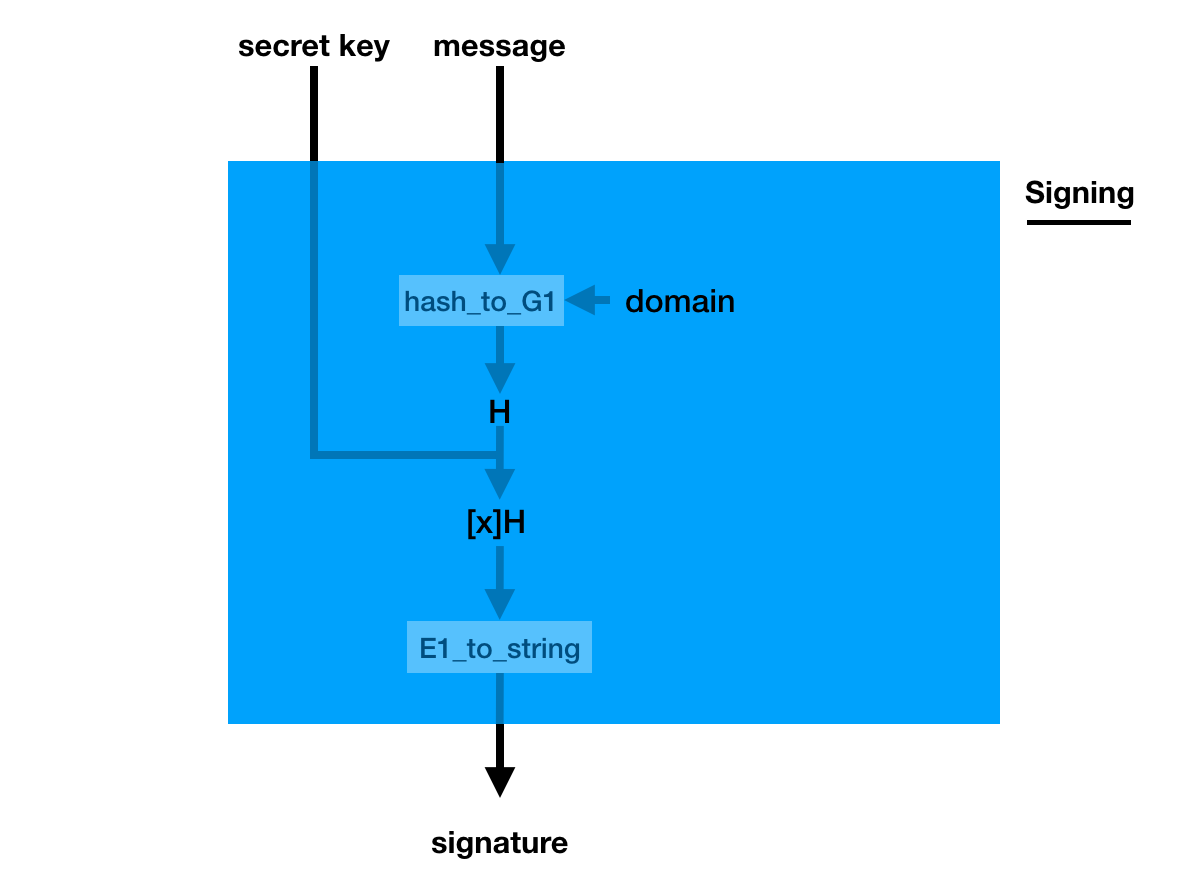
The signature is a bit weird though, you pretend the hashed message is the generator (using a hash_to_G1 function you hash the message into a point on a curve) and you do what you usually do in a key generation: you make it a public key with your private key
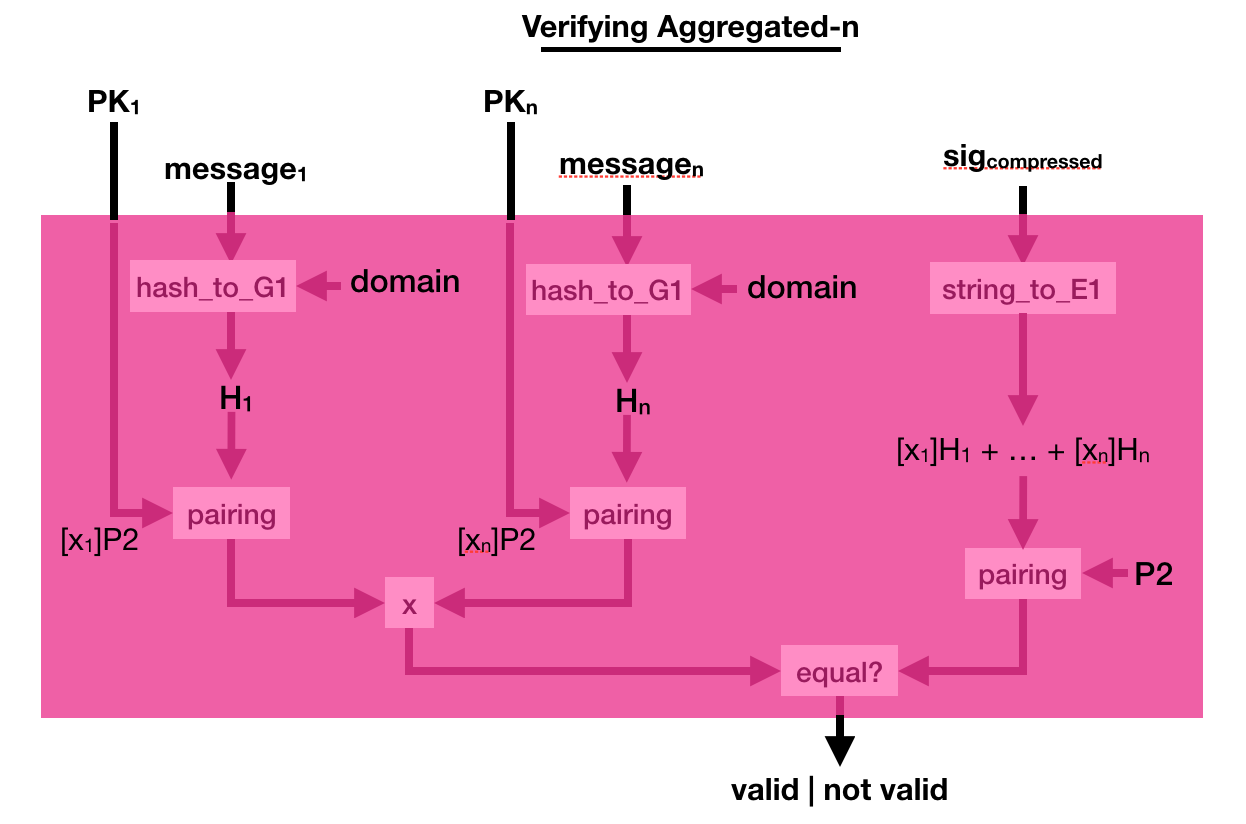
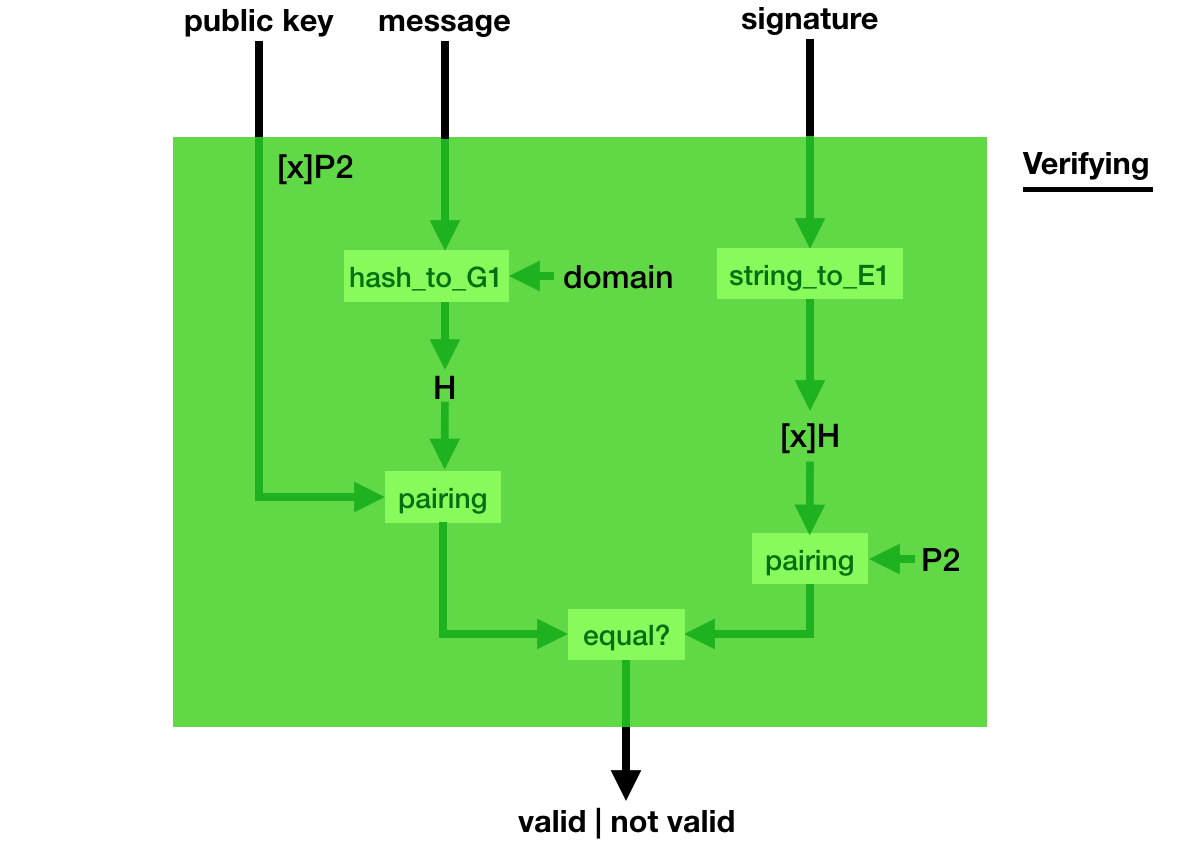
Verification is even weirder, you use a bilinear pairing to verify that indeed, pairing([secret_key]hashed_msg, P2) = pairing([secret_key]P2, hashed_msg).
This weird signing/verifying process allows for pretty cool stuff. You can compress (aggregate) signatures of the same msg in a single signature!
To do that, simply add all the signatures together! Easy peasy right?
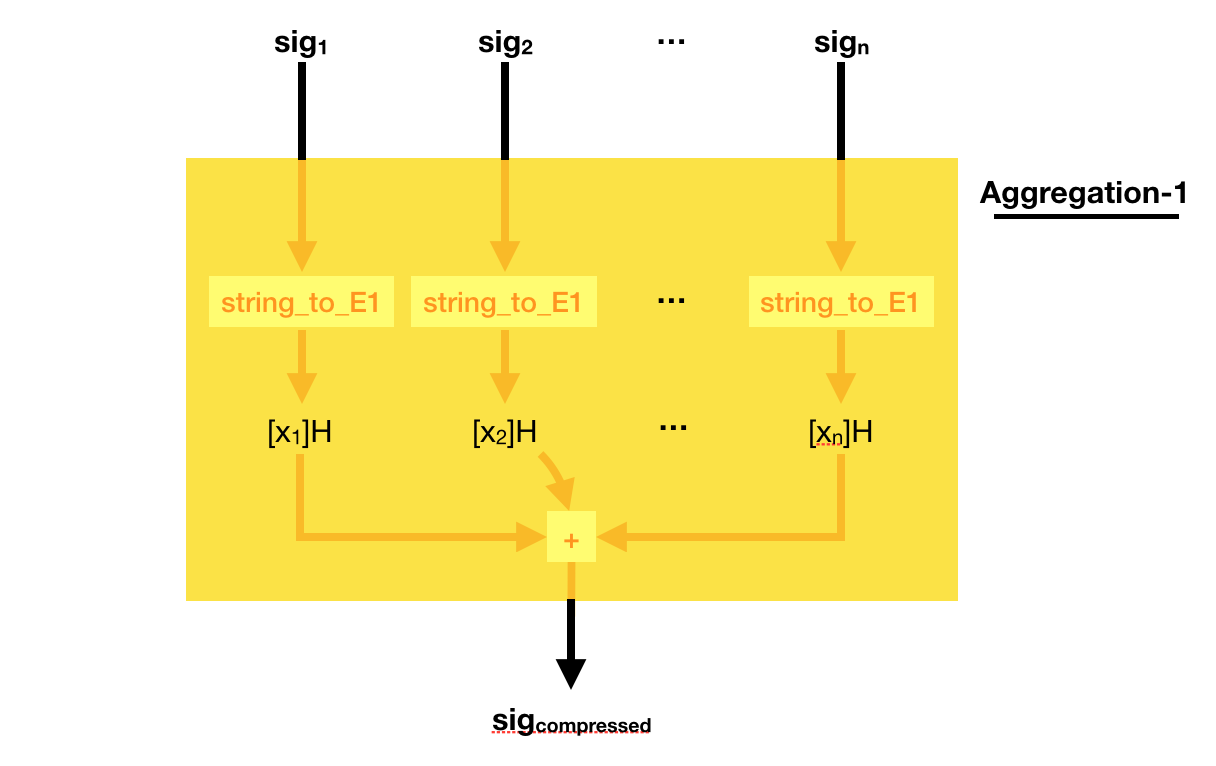
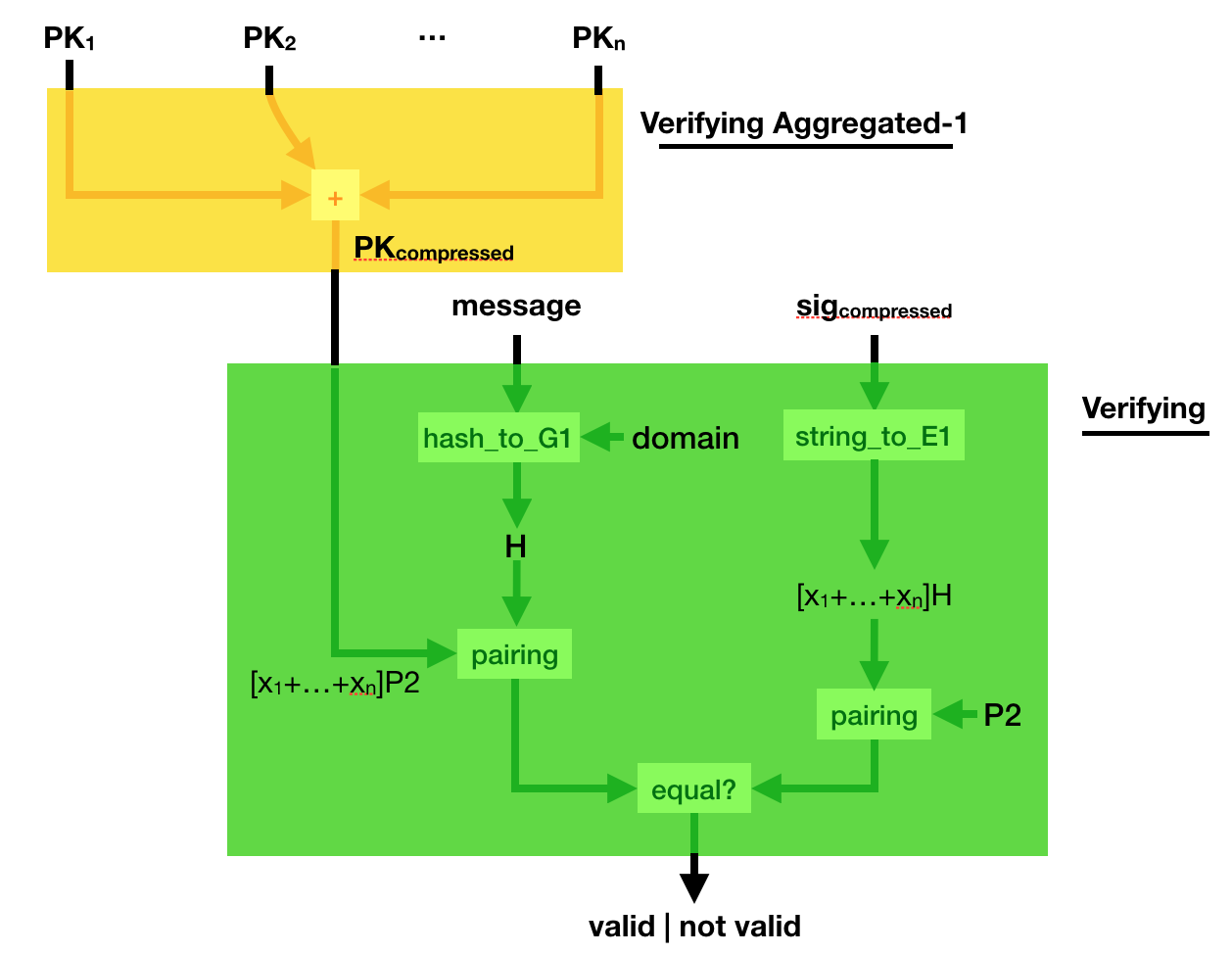
Can you verify such a compressed signature? Yes you can.
Simply compress the public key, the same way you compressed the signature. And verify the sig_compressed with the public_key_compressed. Elegant :)
But what if the different signatures are on different messages? Well, just add them together as well.
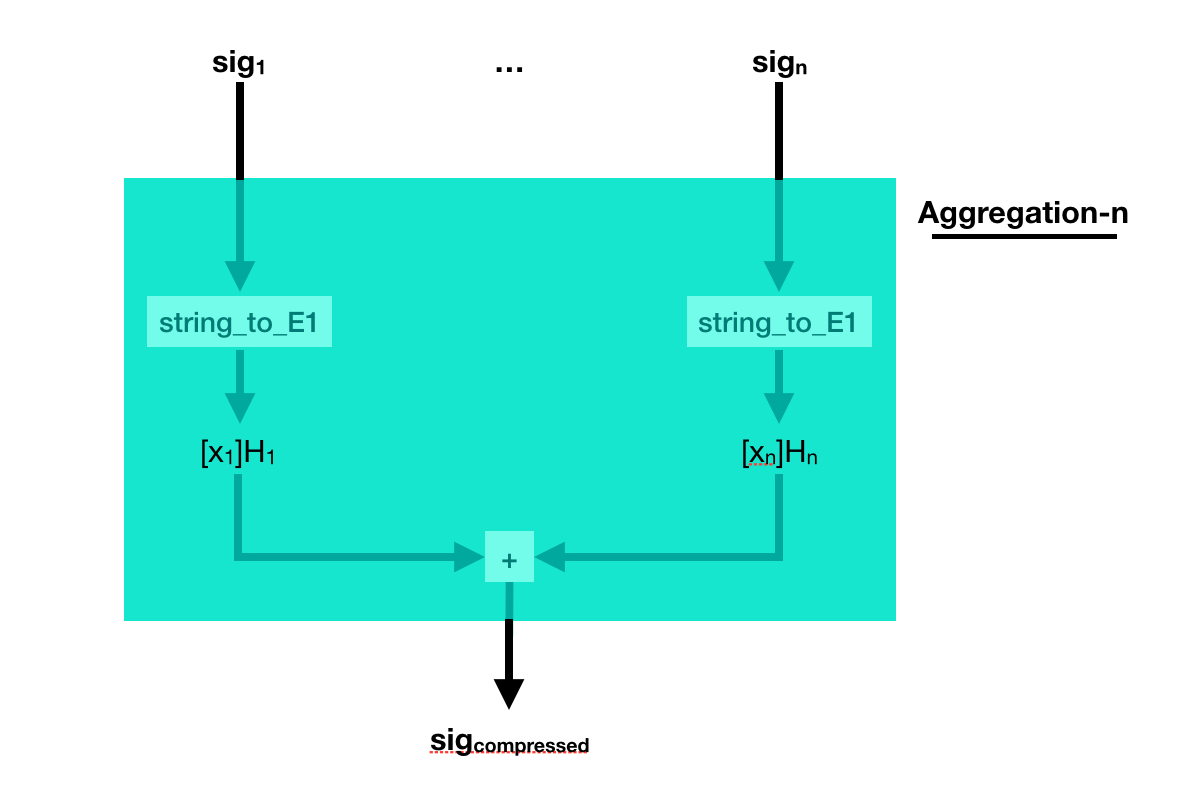
The process to verify that is a bit more complicated. This time you multiply a bunch of pairing([secret_key]P2, hashed_msg) together, and you verify that it is equal to another pairing made out of the compressed signature. Pairings are magical!