Quick access to articles on this page:
more on the next page...
I've talked about iterative constraint systems in the past, which I really like as an abstraction to build interactive (and then non-interactive) proof systems. But I didn't really explain the kind of circuits you would implement using iterative constraint systems (besides saying that these would be circuits to implement permutations or lookup arguments).
Just to recap in a single paragraph the idea of iterative constraint system: they are constraint system where the prover fills the value of the witness registers (also called columns or wires) associated with a circuit, then ask for challenge(s), then fills the value of new registers associated with a new circuit. That new circuit is more powerful as it can also make use of the given challenge(s) as constant(s) and the previous witness registers.
Well I think here's one generalization that I'm willing to make (although as with every generalization I'm sure someone will find the exception to the rule): any iterative circuit implements a Schwartz-Zippel circuit. If you don't know about the Schwartz-Zippel lemma, it basically allows you to check that two polynomials $f$ and $g$ are equal on every point $x \in S$ for some domain $S$ (usually the entire circuit evaluation domain) by just checking that they are equal at a random point $r$. That is, $f(r) = g(r)$.
So my generalization is that the challenge(s) point(s) I mentioned above are always Schwartz-Zippel evaluation points, and any follow up iterative circuit will always compute the evaluation of two polynomials at that point and constrain that they match. Most of the time, there's actually no "final" constraint that checks that two polynomials match, instead the polynomial $f(x) - g(x)$ is computed and check to be equal to 0, or the polynomial $f(x)/g(x)$ is computed and checked to be 1.
This is what is done in the plonk permutation, for example, as I pointed out here.
Exercise: in the plonk permutation post above, would the iterative circuit be as efficient if it was written as the separate evaluation of $f$ and $g$ at the challenge points, and then a final constraint would check that they match?
EDIT: Pratyush pointed me to a paper (Volatile and Persistent Memory for zkSNARKs via Algebraic Interactive Proofs) that might introduce a similar abstraction/concept under the name algebraic Interactive Proofs (AIP). It seems like the Hekaton codebase also has an user-facing interface to compose such iterative circuits.
Here's a short note on the Montgomery reduction algorithm, which we explained in this audit report of p256. If you don't know, this is an algorithm that is used to perform modular reductions in an efficient way. I invite you to read the explanations in the report, up until the section on word-by-word Montgomery reduction.
In this note, I wanted to offer a different explanation as to why most of the computation happens modulo $b$ instead of modulo $R$.
As a recap, we want to use $A$ (called $\bar{x}$ in the report's explanations) in a base-$b$ decomposition so that in our implementation we can use limbs of size $b$:
$$
A = a_0 + a_1 \cdot b + a_2 \cdot b^2 + \cdots
$$
Knowing that we can write the nominator part of $N/R$ as explained here as:
$$
N = (a_0 + a_1 \cdot b + a_2 \cdot b^2 + \cdots) + k \cdot m
$$
Grouping by $b^i$ terms we get the following terms:
$$
N = (a_0 + k_0 \cdot m) + b \cdot (a_1 + k_1 \cdot m) + b^2 \cdot (a_2 + k_2 \cdot m) + \cdots
$$
but then why do algorithms compute $k_i = a_i m^{-1} \mod b$ at this point?
The trick is to notice that if a value is divisible by a power of 2, let's say $2^l$, then it means that the first $l$ least-significant bits are 0.
As such, the value $A + k \cdot m$ we are computing in the integers will have the first $n$ chunks sum to zero if it wants to be divisible by $R = b^n$ (where $b$ is a power of 2):
$$
\sum_{i=0}^{n-1} b^i \cdot (a_i + k_i \cdot m) = 0
$$
This means that:
- either $a_i + k_i \cdot m = 0$ (each term will separately be 0)
- or $a_i + k_i \cdot m = b \cdot \text{carry}$ (cancellation will occur with carries except for the last chunk that needs to be 0)
In both case, we can write:
$$
a_i + k_i \cdot m = 0 \mod b
$$
By now there's already a number of great explanation for Plonk's permutation argument (e.g. my own here, zcash's). But if it still causes you trouble, maybe read this visual explanation first.
On the left of this diagram you can see the table created by the three wires (or columns) of Plonk, with some added colors for cells that are wired to one another. As you can see, the values in the cells are valid: they respect the wiring (two cells that are wired must have the same values). Take a look at it and then read the next paragraph for an explanation of what's happening on the right:

On the right, you can see how we encode a permutation on the columns and rows to obtain a new table that, if the wiring was respected, should be the exact same table but with a different ordering.
The ordering will be eliminated in the permutation argument of Plonk, which will just check that both tables contain the same rows.
To encode the tables, we use two techniques illustrated in this diagram:
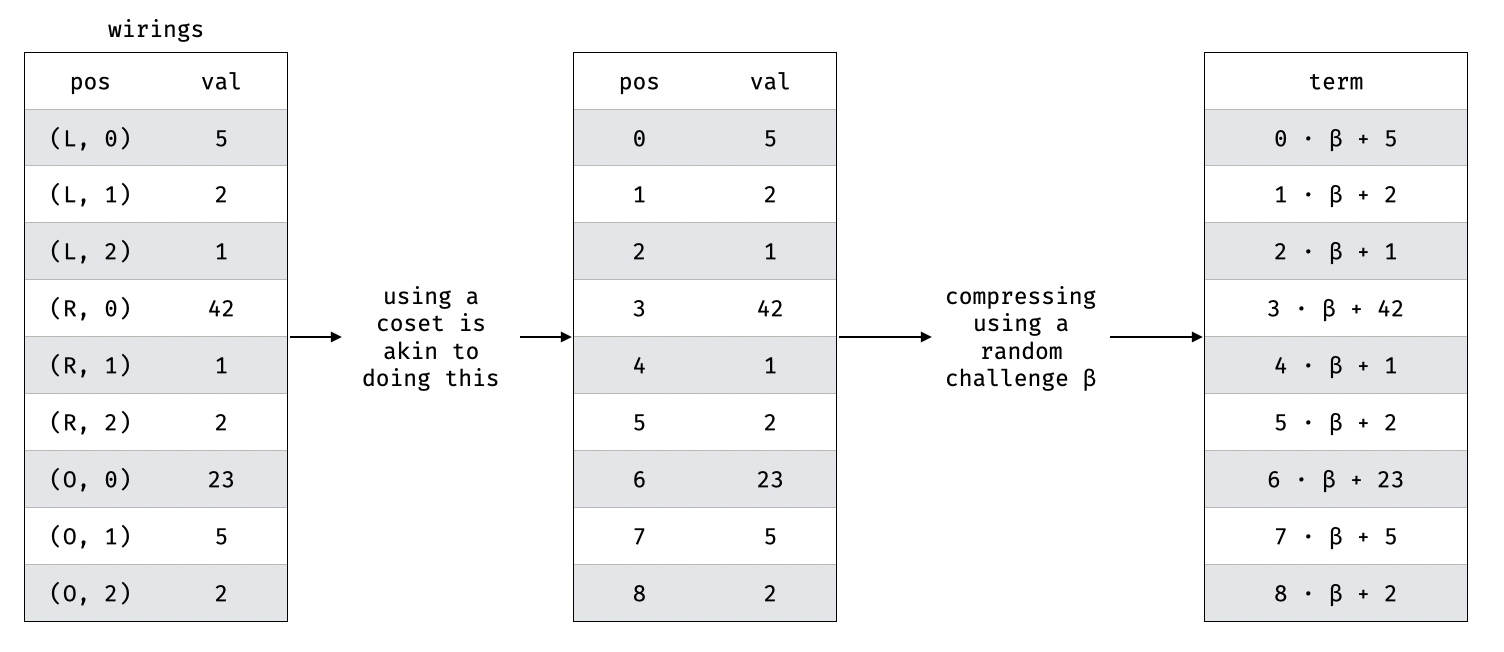
The first one is to use different cosets (i.e. completely distinct sets of points) to represent the different columns and rows. This is most likely the more confusing step of the permutation and so I've illustrated it with what it does in essence (assign a unique "index" that we can use to refer to each value).
The second one is simply to compress multiple columns with a challenge. (This technique is used in lookups as well when lookup tables have multiple columns.)
The following permutation circuit is then implemented:
def pos(col, row):
return cosets[col] * row
def tuple(col, row, separator, value):
return pos(col, row) * separator + value
# ((0, i), a[i]) * ((1, i), b[i]) * ((2, i), c[i])
def f(row, registers, challenges):
return tuple(0, row, challenges[BETA], registers[0][row]) * tuple(1, row, challenges[BETA], registers[1][row]) * tuple(2, row, challenges[BETA], registers[2][row])
# (perm(0, i), a[i]) * (perm(1, i), b[i]) * (perm(2, i), c[i])
def g(row, registers, challenges):
col0, row0 = circuit_permutation(0, row)
col1, row1 = circuit_permutation(1, row)
col2, row2 = circuit_permutation(2, row)
return tuple(col0, row0, challenges[BETA], registers[0][row]) * tuple(col1, row1, challenges[BETA], registers[1][row]) * tuple(col2, row2, challenges[BETA], registers[2][row])
Z = 4
def compute_accumulator(row, registers, challenges):
# z[-1] = 1
if row == -1:
assert registers[Z][row] == 1
return
# z[0] = 1
if row == 0:
assert registers[Z][row] == 1
# z[i+1] = z[i] * f[i] / g[i]
registers[Z][row+1] = registers[Z][row] * f(row, registers, challenges) / g(row, registers, challenges)
where the circuit is an AIR circuit built iteratively. That is, it was iteratively built on top of the first 3 registers. This means that the first 3 registers are now read-only (the left, right, and output registers of Plonk), whereas the fourth register (Z) can be written to. Since it's an AIR, things can be read at and written to at different adjacent rows, but as there is a cost to pay we only use that ability to write to the next adjacent row of the Z register.
To understand why the circuit looks like this, read the real explanation.
I already wrote about the linearization technique of plonk here and here. But there's a more generalized and high-level view to understand it, as it's being used in many protocols (e.g. Shplonk) as well.
Imagine you have the following check that you want to do:
$$f(x) \cdot g(x) \cdot h(x) + 3 \cdot m(x) + 7 = 0$$
but some of these polynomials contain secret data, what you do is that you use commitments instead:
$$[f(x)] \cdot [g(x)] \cdot [h(x)] + 3 \cdot [m(x)] + 7 \cdot [1] = [0]$$
now it looks like we could do the check within the commitments and it could work.
The problem is that we can't multiply commitments, we can only do linear operations with commitments! That is, operations that preserves scaling and addition.
So we give up trying to do the check within the commitments, and we instead perform the check in the clear! That is, we try to perform the following check at a random point $z$ (this is secure thanks to Schwartz-Zippel):
$$f(z) \cdot g(z) \cdot h(z) + 3 \cdot m(z) + 7 = 0$$
To do that, we can simply ask a prover to produce evaluations at $z$ (accompanied with evaluation proofs) for each of the commitments.
Note that this leaks some information about each committed polynomials, so usually to preserve zero-knowledge you'd have to blind these polynomials
But Plonk optimizes this by saying: we don't need to evaluate everything, we can just evaluate some of the commitments to obtain a partial evaluation. For example, we can just evaluate $f$ and $g$ to obtain the following linear combination of commitments:
$$
f(z) \cdot g(z) \cdot [h] + 3 \cdot [m] + 7 \cdot [1]
$$
This semantically represents a commitment to the partial evaluation of a polynomial at a point $z$. And at this point we can just produce an evaluation proof that this committed polynomial evaluates to 0 at the point $\textbf{z}$.
Since we are already verifying evaluation proofs (here of $f$ and $g$ at $z$), we can simply add another evaluation proof to check to that list (and benefit from some batching technique that makes it look like a single check).
That's it, when you're stuck trying to verify things using commitments, just evaluate things!
As a security consultant you're most of the time forced to do something that no developers do: you're forced to become an expert in a codebase without writing a single line of code, and that in a short amount of time.
But let me say that it's of course not entirely true that you should not write code. I actually think part of understanding something deeply means playing with it. Researchers know that very well, as they spend a lot of their time implementing the papers they're trying to understand, asking themselves questions about the subject they're studying ("what would happen if I look in a mirror while traveling at the speed of light?"), doing written exercises like we used to do in Math classes. So as a consultant, you of course benefit from playing with the code you're looking at.
But that's not what I want to talk about today. What I want to talk about is how flawed the top-down approach is. I know it very well because this is how I audited code for way too long. And it's only when I realized, looking at the people that were inspiring me throughout my career, that the pros don't do that. The pros do bottom-up.
What's wrong with top-down though? I think the problem is that it's a trap and a time sink that brings very little benefit. The ROI is rapidly diminishing as you usually do very little deep work when surveying things from a high-level point of view, and can easily get the feeling of being busy when really what you're doing is spending time learning about things that won't matter eventually.
What matters is the core, the actual nitty gritty details, the algorithms implemented. What I've seen every talented engineer do when they want to dive into some code is to spend a lot of time in one place, focusing on understanding and mastering a self-contained part of the codebase.
Once they understand it, then they move to another part of the code, increasing their scope and their understanding of the project. By doing that several time, you quickly realize you know more than everybody, including some of the developers behind the code you're looking at. Not only that, it is only when you do that deep work in one place that you can accumulate real knowledge and that you end up finding good bugs.
Perhaps a last note on the top-down approach: it's a much more relaxed and rewarding process. You can really feel like you're never really learning important knowledge when you spent too much time at a high-level, and you can also easily feel overwhelmed that you'll never have the time to look at everything.
This is very human: if you could see any large project from a bird’s-eye view, you would quickly get discouraged and want to give up before even starting. Imagine a marathon runner visualizing the entirety of what they have to run while they're running their first 10 minutes. This is what they tell you not to do!
The bottom-up approach gives you the illusion that the scope you're looking at is not that big, and so as you focus on what's in front of you you can be more productive by not being distracted by the enormity of the project. And it's more fun as well!
This is somehow related but I've always thought that telling you all about the context of a story instead of showing it to you, in books or in movies, is lazy writing. I've always criticized the long textual intros of StarWars movies that take that idea to the extreme, and I've never understood why they kept that gimmick in all other StarWars movies in spite of being the IP's signature is also one of its worse features. That's an extreme top-down approach! Boring!
Check out https://blog.zksecurity.xyz/posts/internship-2025/
Looking for an internship in ZK, MPC, FHE, and post-quantum cryptography? Interested in working with AI, formal verification, and TEEs? We are always looking for talented peeps to join our team and do interesting research!
I tried to record a few short videos these last months (eventhough the last one is quite long). You might enjoy some of them:
I dropped the "vlog" on the last one (that's 45min long!) so you don't feel like you're wasting your time listening to me. The second one is a bit shameful to me because my habit of working out has dwindled down dramatically and I'm now fighting to preserve it while enduring the long winter of New York :D
If you have missed me, I was in different places on the Internet and in real life. Here are three whiteboard sessions on different aspects of zero-knowledge:



