Quick access to articles on this page:
more on the next page...

In late 2008, 64 candidates took part in NIST's hashing competition, fighting to replace the SHA-2 family of hash functions.
Keccak won the SHA-3 competition, and became the FIPS 202 standard on August 5, 2015.
All the other contenders lost. The final round included Skein, JH, Grøstl and BLAKE.
Interestingly in 2012, right in the middle of the competition, BLAKE2 was released. Being too late to take part in the fight to become SHA-3, it just stood on its own awkwardly.
Fast forward to this day, you can now read an impressive list of applications, libraries and standards making use of BLAKE2. Argon2 the winner of the Password Hashing Competition, the Noise protocol framework, libsodium, ...
On their page you can read:
BLAKE2 is a cryptographic hash function faster than MD5, SHA-1, SHA-2, and SHA-3, yet is at least as secure as the latest standard SHA-3. BLAKE2 has been adopted by many projects due to its high speed, security, and simplicity.
And it is indeed for the speed that BLAKE2 is praised. But what exactly is BLAKE2?
BLAKE2 relies on (essentially) the same core algorithm as BLAKE, which has been intensively analyzed since 2008 within the SHA-3 competition, and which was one of the 5 finalists. NIST's final report writes that BLAKE has a "very large security margin", and that the the cryptanalysis performed on it has "a great deal of depth". The best academic attack on BLAKE (and BLAKE2) works on a reduced version with 2.5 rounds, whereas BLAKE2b does 12 rounds, and BLAKE2s does 10 rounds. But even this attack is not practical: it only shows for example that with 2.5 rounds, the preimage security of BLAKE2b is downgraded from 512 bits to 481 bits, or that the collision security of BLAKE2s is downgraded from 128 bits to 112 bits (which is similar to the security of 2048-bit RSA).
And that's where BLAKE2 shines. It's a modern and secure hash function that performs better than SHA-3 in software. SHA-3 is fast in hardware, this is true, but Intel does not have a good track record of quickly implementing cryptography in hardware. It is only in 2013 that SHA-2 joined Intel's set of instructions, along with SHA-1...
What is being done about it?
Some people are recommending SHAKE. Here is what the Go SHA-3 library says on the subject:
If you aren't sure what function you need, use SHAKE256 with at least 64 bytes of output. The SHAKE instances are faster than the SHA3 instances; the latter have to allocate memory to conform to the hash.Hash interface.
But why is SHA-3 slow in software? How can SHAKE be faster?
This is because SHA-3's parameters are weirdly big. It is hard to know exactly why. The NIST provided some vague explanations. Other reasons might include:
- Not to be less secure than SHA-2. SHA-2 had 256-bit security against pre-image attacks so SHA-3 had to provide the same (or at least a minimum of) 256-bit security against these attacks. (Thanks to Krisztián Pintér for pointing this out.)
- To be more secure than SHA-2. Since SHA-2 revealed itself to be more secure than we previously thought, there was no reason to develop a similar replacement.
- To give some credits to the NIST. In view of people's concerns with NIST's ties with the NSA, they could not afford to act lightly around security parameters.
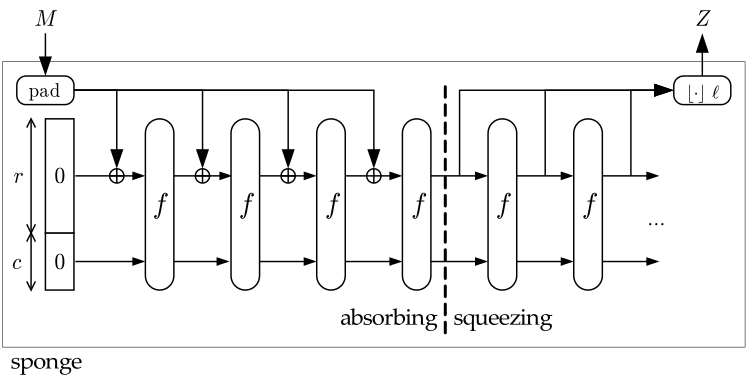
The following table shows the parameters of the SHAKE and SHA-3 constructions. To understand them, you need to understand two of the parameters:
- The rate (
r): it is the block size of the hash function. The smaller, the more computation will have to be done to process the whole input (more calls to the permutation (f)).
- The capacity (
c): it is the secret part of the hash function. You never reveal this! The bigger the better, but the bigger the smaller is your rate :)
| algorithm | rate | capacity | mode (d) | output length (bits) | security level (bits) |
| SHAKE128 | 1344 | 256 | 0x1F | unlimited | 128 |
| SHAKE256 | 1088 | 512 | 0x1F | unlimited | 256 |
| SHA3-224 | 1152 | 448 | 0x06 | 224 | 112 |
| SHA3-256 | 1088 | 512 | 0x06 | 256 | 128 |
| SHA3-384 | 832 | 768 | 0x06 | 384 | 192 |
| SHA3-512 | 576 | 1024 | 0x06 | 512 | 256 |
The problem here is that SHA-3's capacities is way bigger than it has to be.
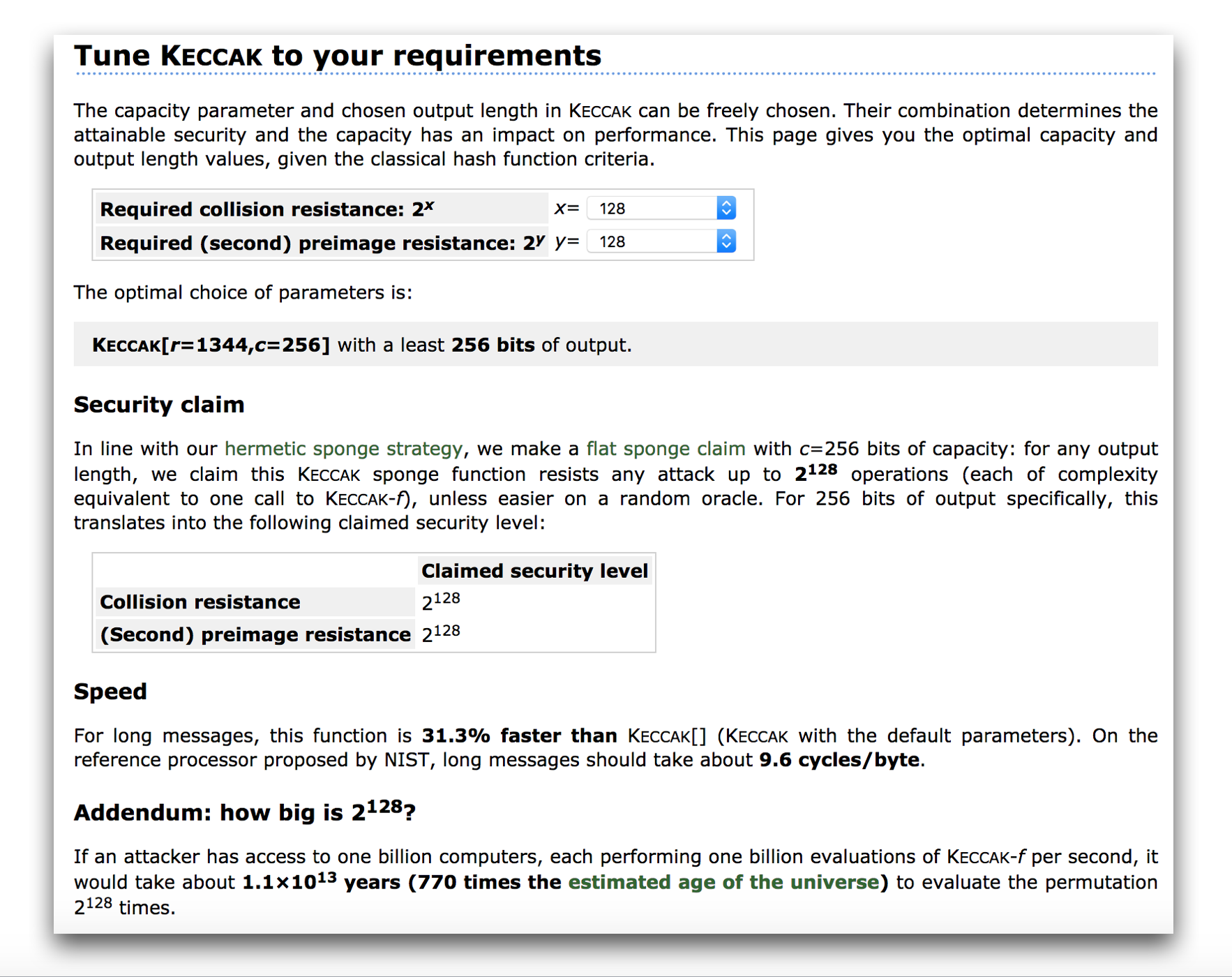
512 bits of capacity (secret) for SHA3-256 provides the square root of security against (second pre-image attacks (that is 256-bit security, assuming that the output used is long enough). SHA3-256's output is 256 bits in length, which gives us the square root of security (128-bit) against collision attacks (birthday bound). We end up with the same theoretical security properties of SHA-256, which is questionably large for most applications.
Keccak even has a page to tune its security requirements which doesn't advise such capacities.
Is this really the end?
Of course not. In the end, SHA-3 is a big name, people will use it because they hear about it being the standard. It's a good thing! SHA-3 is a good hash function.
People who know what they are doing, and who care about speed, will use BLAKE2 which is equally as good of a choice.
But these are not the last words of the Keccak's team, and not the last one of this blog post either. Keccak is indeed a surprisingly well thought construction relying on a single permutation. Used in the right way it HAS to be fast.
Mid-2016, the Keccak team came back with a new algorithm called KangarooTwelve. And you might have guessed, it is to SHA-3 what BLAKE2 is to BLAKE.
It came with 12 rounds instead of 24 (which is still a huge number compared to current cryptanalysis) and some sane parameters: a capacity of 256 bits like the SHAKE functions.
Tree hashing, a feature allowing you to parallelize hashing of large files, was also added to the mix! Although sc00bz says that they do not provide a "tree hashing" construction but rather a" leaves stapled to a pole" construction.
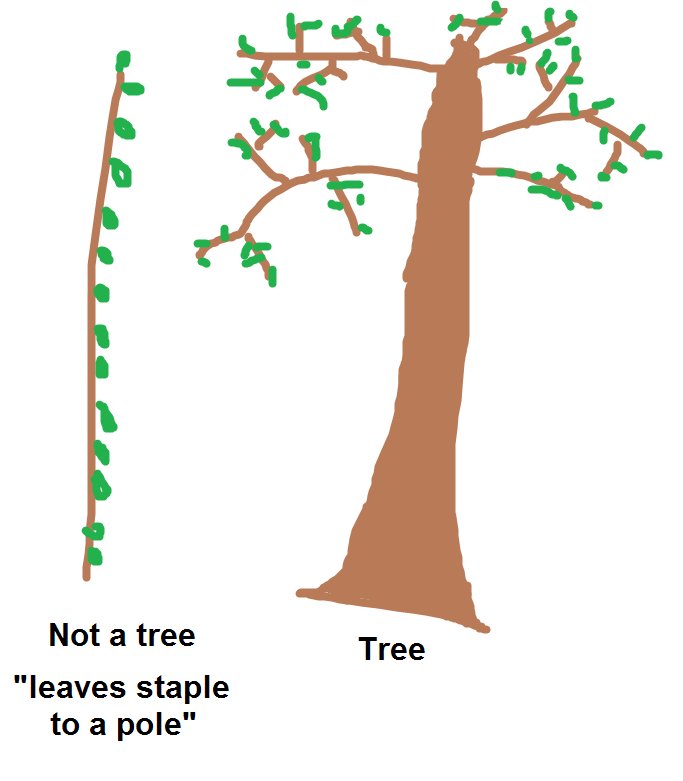
credit: sc00bz
Alright, how does KangarooTwelve work?
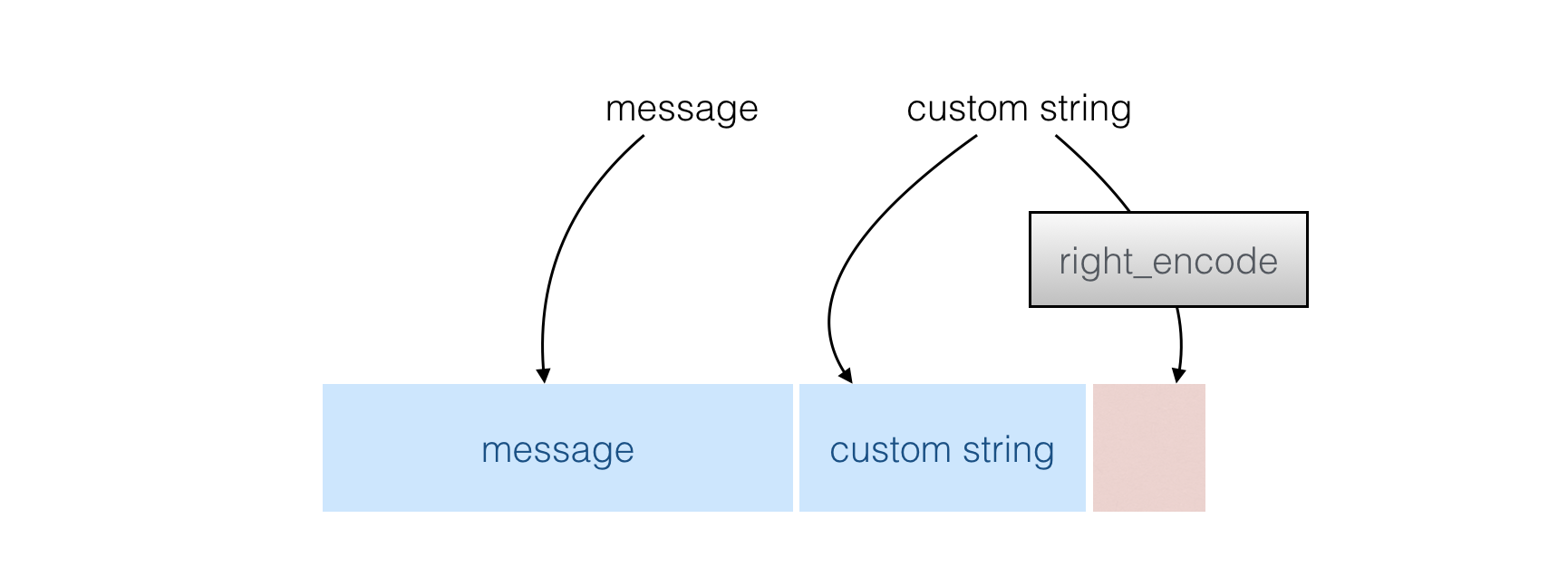
→ First your input is mixed with a "customization string" (which allows you to get different results in different contexts) and the encoding of the length of the customization string (done with right_encode())
→ Second if the message is "short" (≤8192bytes), the tree hashing is not used. The previous blob is padded and permuted with the sponge. Here the sponge call is Keccak with its default multi-rate padding 101*. The output can be as long as you want like the SHAKE functions.
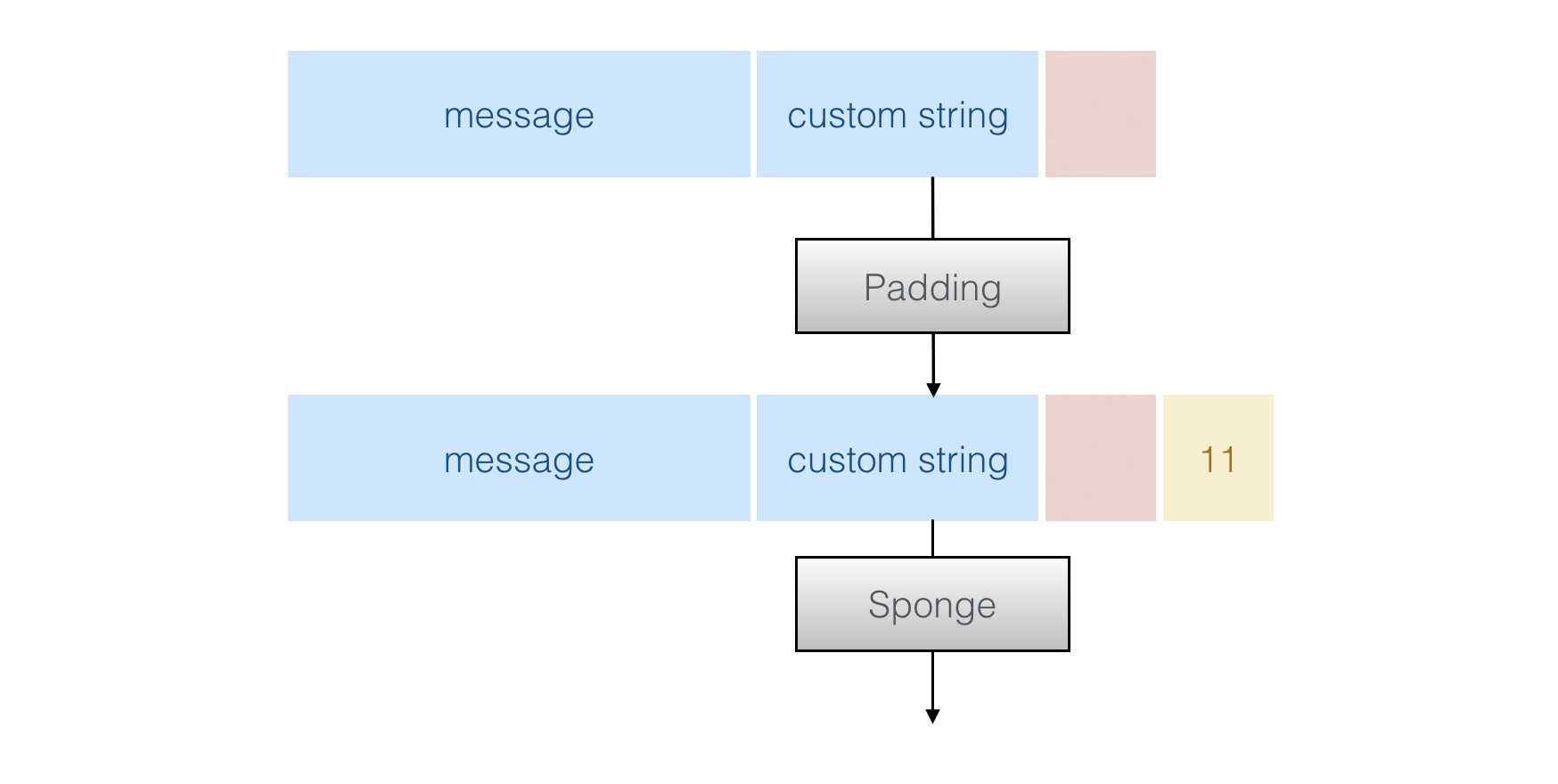
→ Third if the message is "long", it is divided into "chunks" of 8192 bytes. Each chunk (except the first one) is padded and permuted (so effectively hashed). The end result is structured/concatenated/padded and passed through the Sponge again.

This allows each different chunk to be hashed in parallel on different cores or via some SIMD magic.
Before you go, here is a simple python implementation and the reference C implementation.
Daemen gave some performance estimations for KangarooTwelve during the rump session of Crypto 2016:
- Intel Core i5-4570 (Haswell) 4.15 c/b for short input and 1.44 c/b for long input
- Intel Core i5-6500 (Skylake) 3.72 c/b for short input and 1.22 c/b for long input
- Intel Xeon Phi 7250 (Knights Landing) 4.56 c/b for short input and 0.74 c/b for long input
Thank-you for reading!
Let me re-introduce STROBE: it's a protocol framework based on the Duplex construction. It's kind of the symmetric part of TLS if you will, where everything depends on what happened previously. Kind of like when Noise uses the hash of the entire transcript to derive new keys.

You can do different things with different "operations". Encrypt some plaintext, generate some MAC, generate some random numbers, etc...
These different operations can be combined to form a protocol, or can be used as stand-alone in your logic. This is one of the beautiful aspect of STROBE (heavily based on the beauty of Keccak): it provides you with numerous primitives with only a few APIs, and thus a very small source code: count 1,046 lines of code for the current reference implementation in C.
But like anything based on Keccak, you need a padding and it has to be complicated :)
Duplex Calls
The initialization of a Strobe object is done with cSHAKE by XOR'ing this data: [1,self.R,1,0,1,12*8, "STROBEv1.0.2"] then permuting the state.
After the initialization, for every duplex call (before a permutation happens) a padding is applied. This successfully allows series of duplex call to be seen as one cSHAKE call. The rest of this article explains how duplex calls work. These duplex calls are made of potentially multiple operations combined with a padding function, which in STROBE is a combination of cSHAKE's padding and STROBE's own padding.
if we just started an operation:
[old_begin, flag, data up until the block size (strobe.R)]
flag is one byte computed from:
- The direction of the message when sending or receiving data (I_0).
- The type of operation.
old_begin is the start of the last operation in the current block. It can be seen as the pos_begin of the previous operation. It is computed as:
- If we're starting an operation in a new block:
0. The older operation happened in a previous block.
- If we’re starting an operation in the same block as the previous operation: the starting position of the previous operation in the current block.
if we have already started an operation:
[data up until the block size (strobe.R)]
when a permutation is called (forced or because we reached the blocksize) append:
[pos_begin, cSHAKE's padding = 0x04, 0x00 ... 0x00, 0x80]
pos_begin is the start of our operation in the current block, it is computed as:
- If we're starting the operation on a fresh block:
1. (At index 0 is the value old_begin which can be seend as the padding of the previous operation.)
- If we've already started the operation and already ran F once:
0, indicating that the operation started in a previous block.
- if we're starting the operation, and we're in the same block of another operation: the position of the new operation (which starts at the flag, not the old_begin)
Examples
Example 1: the second operation starts on a new block
block1[old_begin=0, flag, data_1, ..., data_R-2, pos_begin=1, padding= 0x04, 0x80] // the first operation takes more than one block
block2[data_R-1, pos_begin=0, padding=0x04, 0, ..., 0, 0x80] // end of the first operation (and forced permutation)
block3[old_begin=0, flag, data_1, ..., data_R-3, pos_begin=1, padding=0x04, 0, 0x80] // start of the second operation
Example 2: the second operation starts on the same block as the previous operation
block1[old_begin=0, flag, data_1, ..., data_R-2, pos_begin=1, padding= 0x04, 0x80] // the first operation takes more than one block
block2[data_R-1, old_begin=1, flag, data2_1, pos_begin=2 , padding=0x04, 0, ..., 0, 0x80]
Example 3: three operations in the same block
block1[old_begin=0, flag, data_1, ..., data_R-2, pos_begin=1, padding= 0x04, 0x80] // the first operation takes more than one block
block2[data_R-1, old_begin=1, flag, data2_1, pos_begin=2 , old_begin=2, flag, data3_1, pos_begin=5, padding=0x04, 0, ..., 0, 0x80]
I was at Eurocrypt's workshop in Paris last week. One of the reason is because I really like workshops. It was good. Good because of the Tamarin workshop, less good because it ended up just being like a normal conference, but still good because it was incredibly close to Real World Crypto.
Tamarin is a "protocol" verification tool. You give it a protocol, a set of security properties it should respect and Tamarin gives you a formal proof (using constraints solving) that the security guarantees are indeed provided OR it gives you a counter example (an attack).
By default, the adversary is a Dolev-Yao adversary that controls the network and can delete, inject, modify and intercept messages on the network
The thing is realllyyyy easy to install.
In the morning, Cas Cremers gave us an intro to Tamarin and taught us how to read inputs and outputs of the tool. In the afternoon, Ralf Sasse told us about more complex concepts while forcing us to write some input for Tamarin.
It was a lot of fun. Way more fun than I expected. I have to admit that I came skeptical, and never really considered formal verification as "practical". But this day changed my mind.
In an afternoon I was capable of creating a pretty simple input to model an opportunistic ephemeral Diffie-Hellman key agreement. The input I wrote is available here. (I have made a better one here and Santiago Zanella made one here as well).
You can see a lot of rules describing the possible transitions of the state machine, and a final lemma which is saying "for any created session (where neither a key or a session key has been leaked) a man-in-the-middle attacker cannot influence the protocol to retrieve the session key". Of course this is ugly, and reading it again a week afterwards I see things I want to rewrite, and probably some "pros" are going to cringe... But it worked out! and Tamarin ended up finding the trivial man-in-the-middle attack.
If you want to play with it, check the online manual which is just great. It provides a few examples that quickly get you started. The hardest part, you must have guessed, is to translate your protocol into this Tamarin input language.

Ekr kick started the TLS:DIV workshop last Sunday. "The number of changes since draft 13 is too damn high" read one of the slide. Not wrong I said to myself. I did read draft 18 in its entirety when we had to review Cloudflare's TLS 1.3 implementation, and I tried to keep up with the changes ever since but I can honestly say that I completely failed.
So I thought, why not creating a nice diff that would allow me to go through all these changes just by reading the spec one more time. With the magic of git diff --color-words --word-diff=porcelain -U1000000 and some python I created a nice spec that shows up differences between draft 18 and the latest commit on the github spec.

You can find it here
If you want the same thing for a different draft version say something in the comment section!
Some of you might have seen the answer of this famous stack overflow question what are the differences between a digital signature, a mac and a hash?:
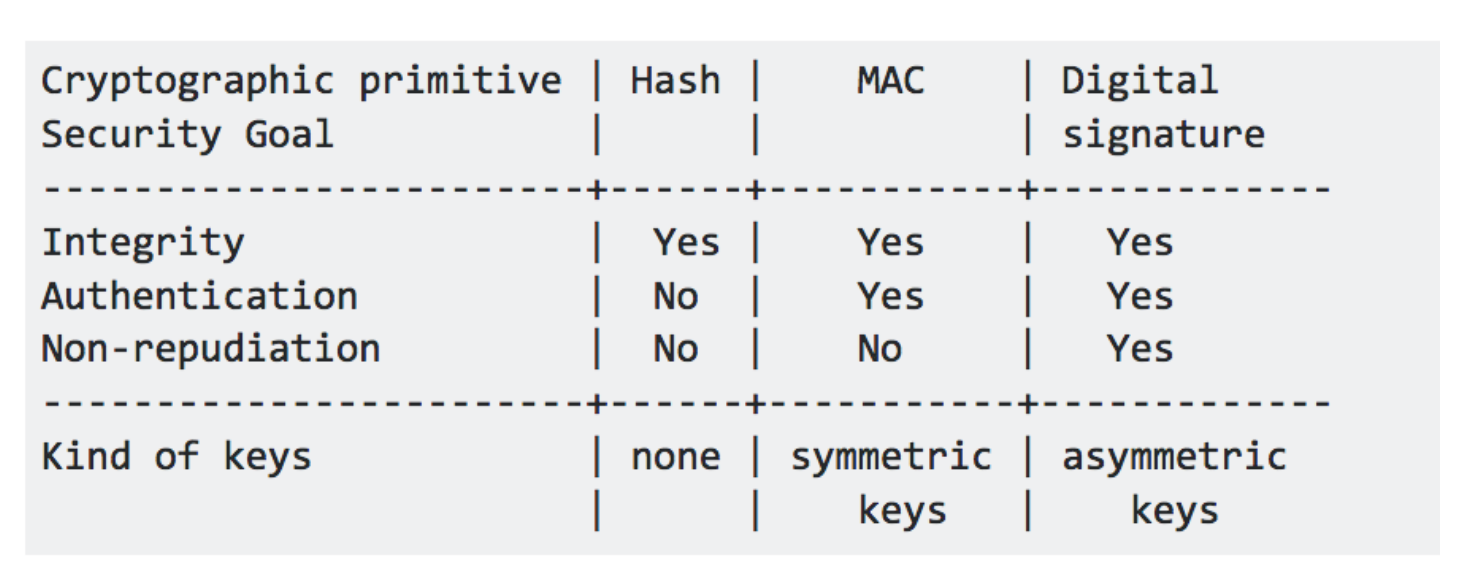
The above table is from the most upvoted answer --but it is false. A hash function does not provide integrity, a MAC provides integrity.
Instead a cryptographic hash function provides three properties, well defined in the world of cryptography: collision resistance, pre-image resistance and second pre-image resistance. Nothing else.

cSHAKE is something to make your own SHAKE! It's defined in this NIST's doc SP 800-185 along other awesome Keccak structures like KMAC (a message authentication code a la hash(key + data) with no length-extension attacks!) and TuppleHash (a hash function to hash structures without ambiguity (fingerprints!)).
And without surprises, it suffers from the same SHA-3 bit ordering problems I talked about in this blogpost and this one as well.
So I thought it would be a good opportunity for me to talk more about SHAKE, cSHAKE and remind you how the bit ordering works!
What is SHAKE?
SHAKE (Secure Hash Algorithm and KECCAK), defined in FIPS 202, is an Extendable-Output Function (or XOF). It's like SHA-3 but with an infinite output. For whatever length you need. You can use that as a KDF, a PRNG, a stream cipher, etc ...
It's based on The Keccak permutation function, and it works pretty much like SHA-3 does. The two differences are that a different domain separator is used (1111 is appended to the input instead of 01 for SHA-3) and you can continue to squeeze the sponge as much as you like (whereas SHA-3 defines how much you should squeeze).
Of course the squeezing will affect the security of your output, if used as a hash you can expect to have 128-bit security against all attacks (including collision resistance) when using an output of 256-bit. If you truncate that down to 128-bit, you will get rid of the collision resistance property but still have (at least) 128-bit security against pre-image attacks. More information is available in the FIPS 202 document where you will find this table in Appendix A:

cSHAKE
SHA-3 and SHAKE were great constructions, but Keccak has so much to offer that the NIST had to release another document: SP 800-185 (for "special publication"). It covers some other constructions (as I said previously), but this is still not the extent of what is possible with Keccak. If you're interested, check KangarooTwelve (which is to SHA-3 what Blake2 is to Blake, a less secure but more efficient hash function), the duplex construction (use the sponge continuously!), Ketje and Keyak (two authenticated encryption modes), ...
SP 800-185 defines cSHAKE as a customable version SHAKE. It works the same except that you have one new input to play with: a customization string. If you've used HKDF before you will quickly get its purpose: avoid collisions between different usages of the Shake function. Here are two examples given by the NIST special publication:
cSHAKE128(input: public_key, output: 256 bits, "key fingerprint"), where "key fingerprint" is the customization string.cSHAKE128(input: email_contents, output: 256 bits, "email signature")
how it works
As with SHAKE, you can choose an output length, here is how the input and the customization string gets fed to the cSHAKE function:
- Use an empty
N string (this is for NIST use only)
- Choose a customization string
S
- apply
encode_string() on the empty string N and on your customization string S
- apply the
bytepad function to both with the rate of the permutation in bytes (168 in the case of cSHAKE128).
- prepend this to your input
- append the bits
00 to your input (domain separator)
KECCAK(bytepad(encode_string(N) || encode_string(S), 168) || input || 00)
What are these functions?
encode_string: left_encode(len(input)) || input.
left_encode: a way to encode a length. It encodes the length of the length, then the length :) all of that in an LSB bit numbering.
bytepad: left_encode(block_size) | input | 0000...0000 with enough 0s for the resulting output to be a byte array multiple of the rate.
The above function can be rewritten:
KECCAK(left_encode(block_size) || left_encode(0) || "" || left_encode(len(S)) || S || 0000...0000 || input || 00)
(This input will then get padded inside of Keccak.)
left_encode
These functions are defined in the special publication NIST document, but they are quite different in the reference implementation).

So here is another explanation on this bit re-ordering trick. Imagine that we have this input to the left_encode function:
0001 0000 | 0011 0001 | 0111 1110
As an hex table it would look like this:
0x10 | 0x31 | 0x7e
Now, the left_encode specification tells us to completely reverse this value, then add a reversed length on the left (here 3). It would look like this:
0111 1110 | 1000 1100 | 0000 1000
1100 0000 | 0111 1110 | 1000 1100 | 0000 1000
This is quite annoying to code. Fortunately, the reference implementation has a trick: it takes the bytes as-is but re-position them following the little endian ordering convention, then add the padding in a natural MSB first bit numbering:
0111 1110 | 0011 0001 | 0001 0000
0000 0011 | 0111 1110 | 0011 0001 | 0001 0000
The Sponge code then re-interprets this in little endian convention:
0001 0000 | 0011 0001 | 0111 1110 | 0000 0011
Which is exactly what was expected, except in reversed order :) which is OK because if you remember correctly from my previous blogpost every operation of the spec is implemented in reversed in the reference implementations.
How to use cSHAKE?
The official Keccak Code Package contains all the keccak functions in C. I've written a Golang version of cShake here that you can put in your golang.org/x/crypto/sha3/ directory, as it hasn't been reviewed by anyone yet I would take this with chopsticks.
As I talked about in a previous blogpost, Keccak and SHA3-3 are different in their bit convention, which gave birth to quite an overly complicated specification. The lack of good explanations in both the reference implementations and the reference documents led me to write this blogpost.
Padding
Before going further, let me briefly re-explain the multi-rate padding also called pad10*1:
- take the input and append the delimiter (
01 for SHA-3)
- append a
1 to start the padding
- append enough
0s followed by a final 1 so that the resulting output is a multiple of the rate
Here is a graphical example with input 0x9c = 1001 1100 and where the rate of our permutation is only 3 bytes:
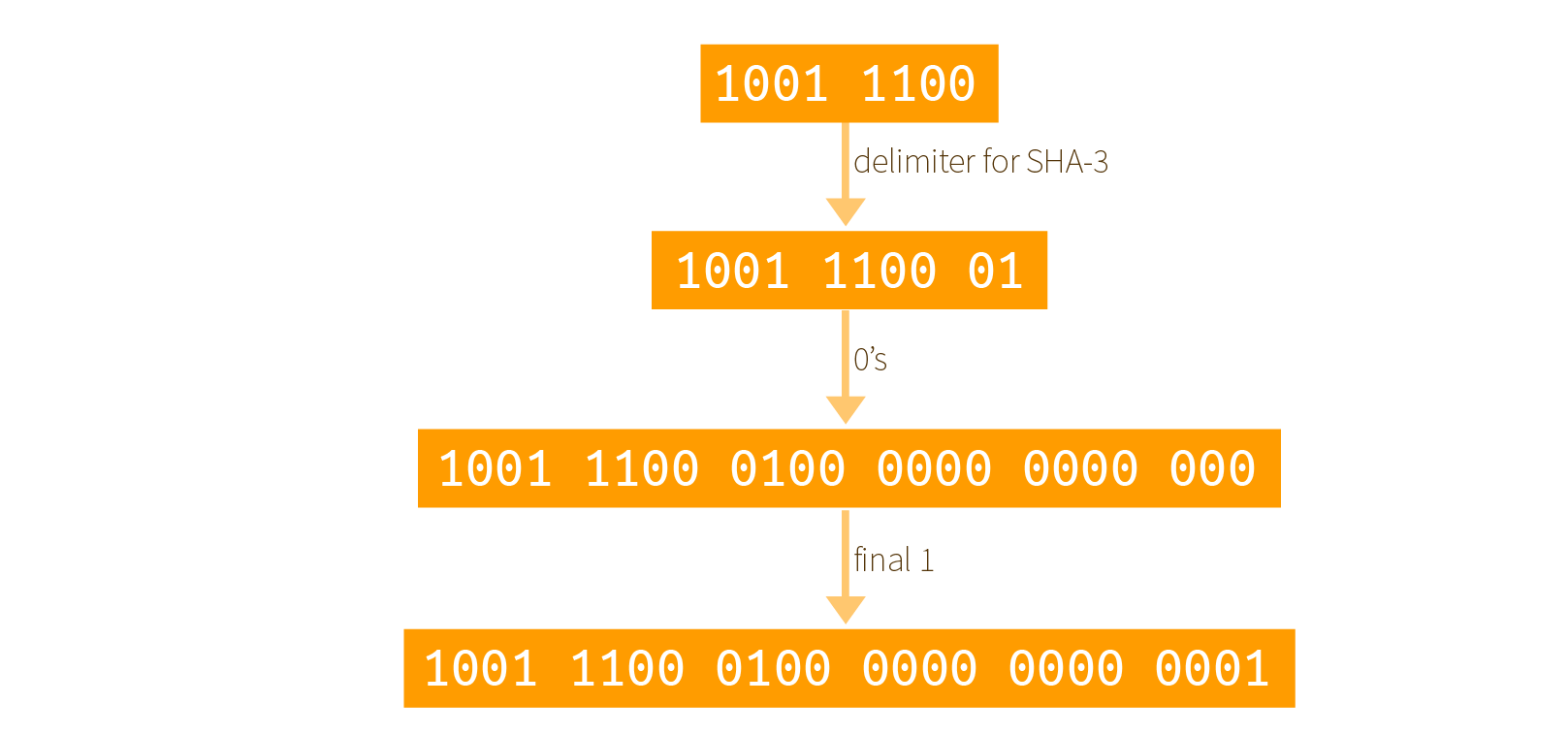
note that I forgot to add a 1 after the delimiter and before all the 0s (thanks Rachel)
Now, I'll just acknowledge that most implementations, and even the specification, talk about using 0x80 for the final bit. This blogpost should answer why.
Theoretical bit numbering
Keccak is specified in term of bits, but is discreetly aware of byte arrays as well. This is important as the rounds of Keccak require us to XOR parts of the input with lanes of the state. These lanes can be represented as uint64 types for keccak-f[1600], which we'll be looking at in this blogpost.
It could be hard to understand what is really going on in FIPS 202, but a look at an older version of the specification shows that Keccak interprets byte arrays in big-endian, but with an LSB bit numbering.
If you look at the Appendix B.1 of FIPS 202. You can see that before an input can be interpreted by SHA-3, it needs to go through some transformations.
Here is our own example of how it works with an input of 0xaebcdf. First the bits are re-mapped, then a padding is added, finally it is split into as many lanes as possible (here we have two 16-bit lanes):
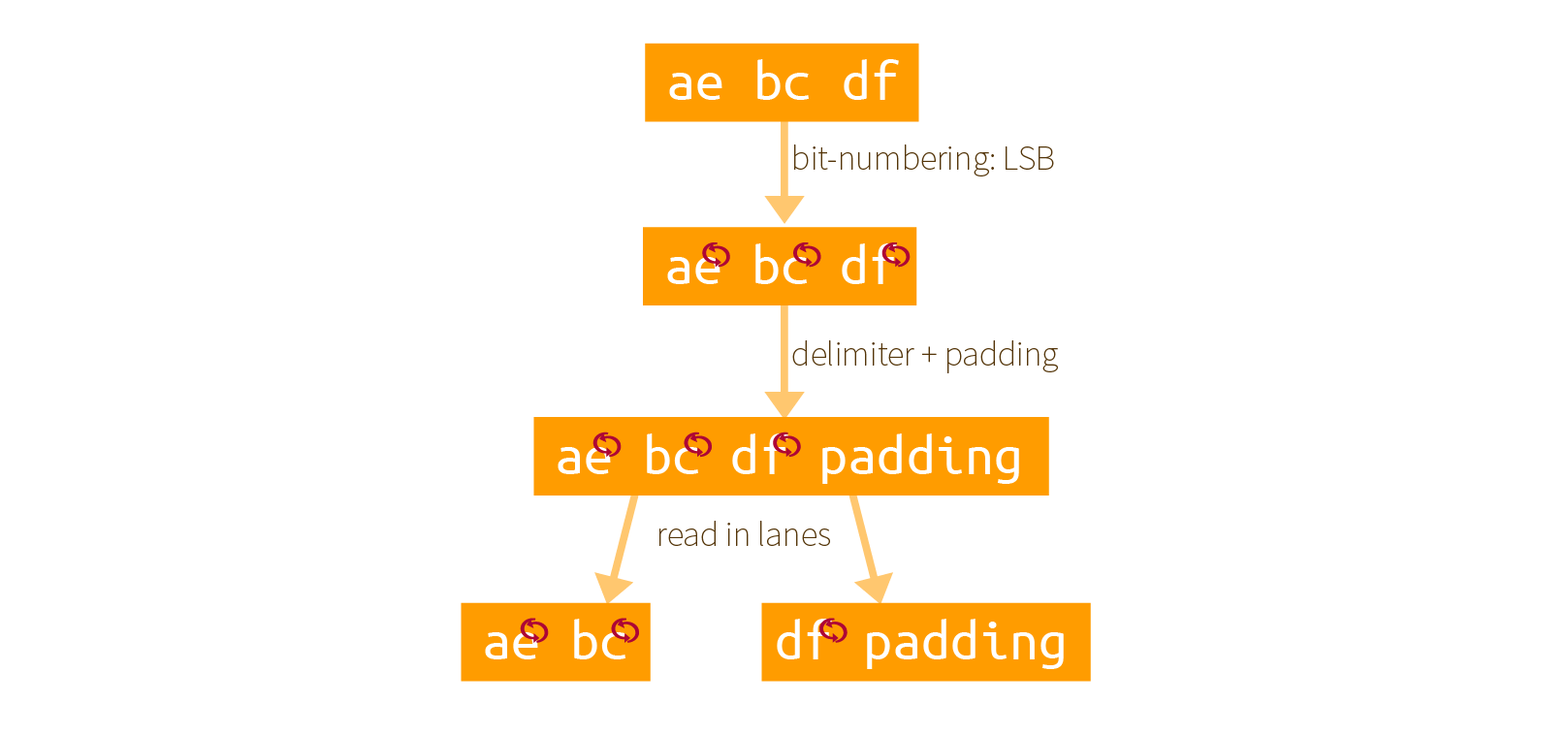
The same examples with bits:
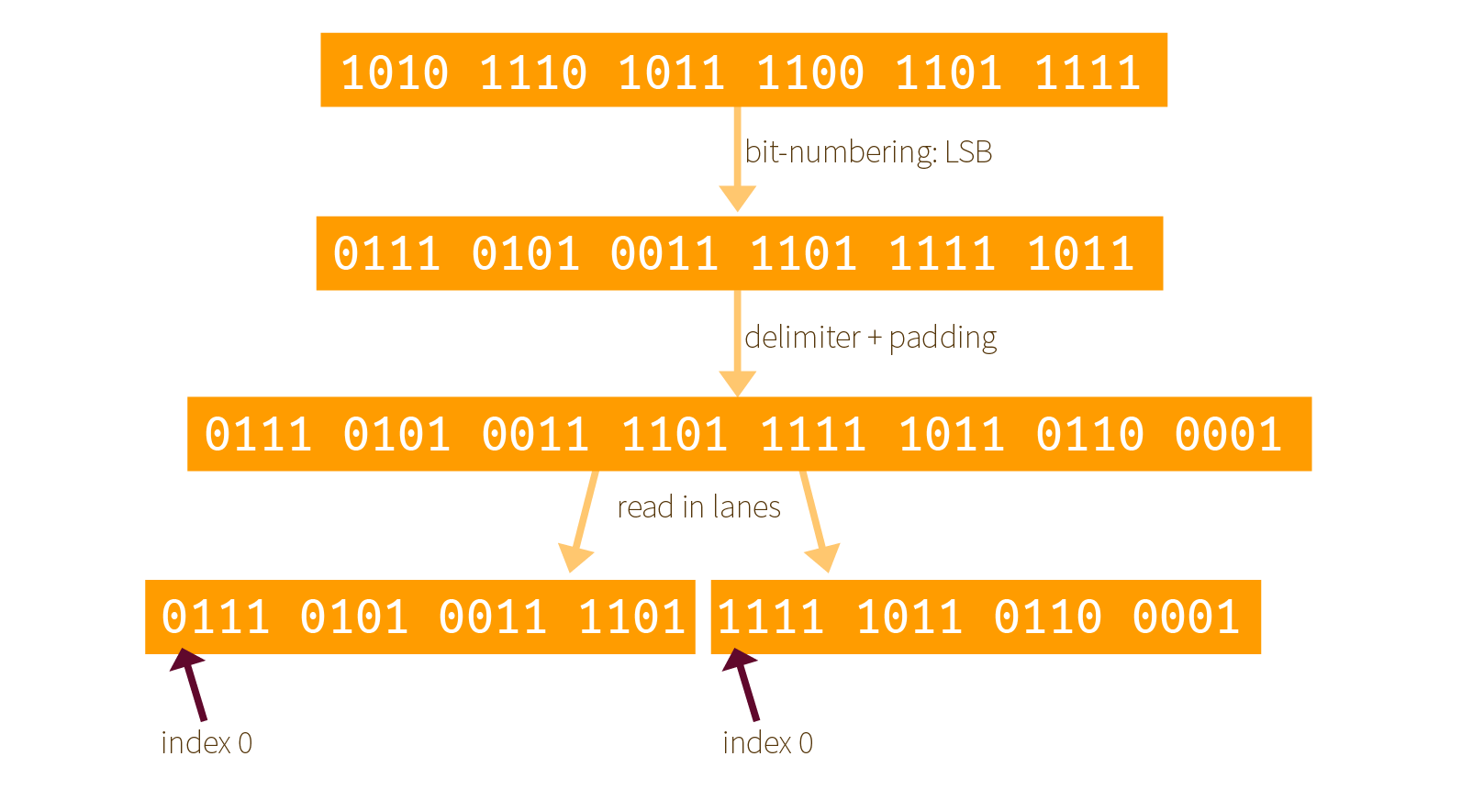
Two things that you must understand here:
- the padding is applied after re-mapping the bits, not before! Since the padding is already defined for Keccak's internal ordering of its bits.
- all of this is done so that a bit string is indexed as LSB first, not MSB first. It's weird but Keccak did it this way.
Why is the indexing of a bitstring so important?
Because we later apply the permutation function on the state, and some of the operations need to know what are the indexes of each bits. More on that later.
How to implement the re-mapping
It must be annoying to reverse all these bits right? What about not doing it? Well brace yourself, there is indeed a clever trick that would allow you to avoid doing this. And this trick is what is used in most of SHA-3's implementations. Here is a graphical explanation of what they do:
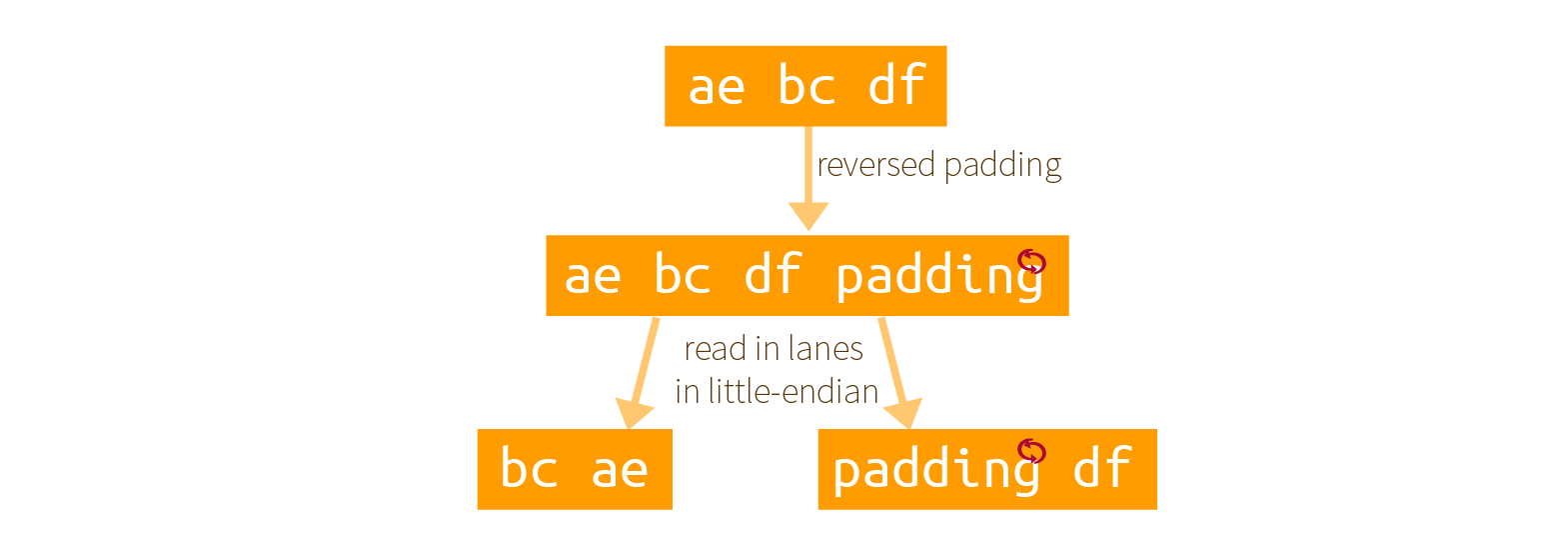
By reading the byte array as little-endian, and using an already reversed delimiter + padding, some magic happens!
The result is exactly the same but in reverse order.
If you aren't convinced look at the following diagram (which shows the same thing with bits) and look at the previous section result. Same, but the bitstream is readable in the reversed direction.
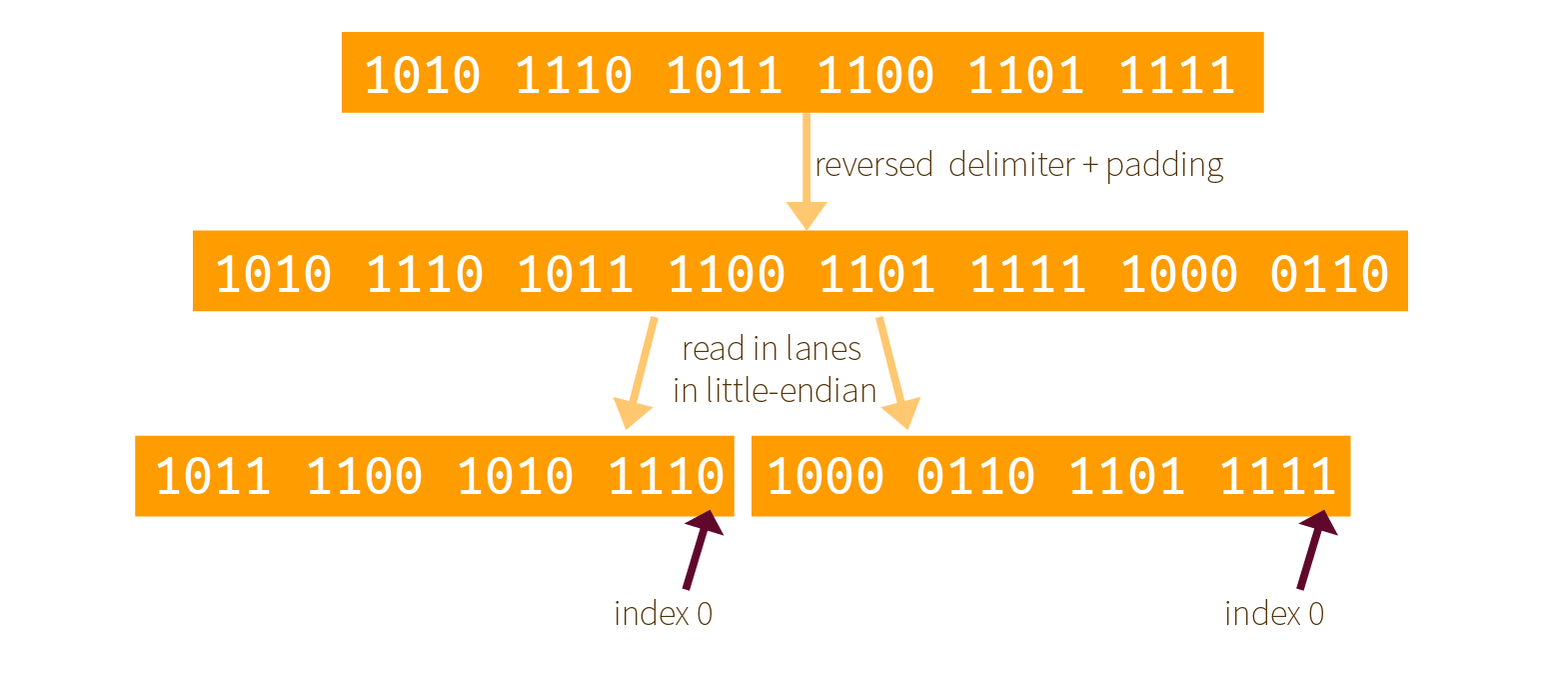
This means that now the index 0 of Keccak's internal ordering is on the right, not on the left. How will it influence the round functions that apply on our lanes?

It turns out that a lot of operations are unchanged. Who would have known that XORs, ANDs and NOTs operations were not affected by the order of the bits! but only some rotations and bit positioning are. If you look at the reference implementations you will see that indeed, rotations have been reversed (compared to what the reference tells you to do).
And this is how a clever implementation trick made its way in a specification with no real explanation.
You're welcome!
"Why is Java a big pile of crap?" said the article. And after reading through the argumentation, I would move to the comment section and read a divergent point of view. Who was right? I wondered. Although everyone knows that Java is indeed a huge pile of crap, many other articles follow the same path of disputing one biased opinion that might be right, wrong, but really is both. I often mused on if I would come to write such a piece, and I think today is the day.
Keccak's (and/or SHA-3's) specification makes no sense.
Yup, it makes no sense, and I have a list of points you'll have to read through to understand how exactly.
By the way, if you didn't know, Keccak was the winner of the SHA-3 competition and blablabla...

Chocoweird indexing
First, let me introduce you to the internal state of Keccak.
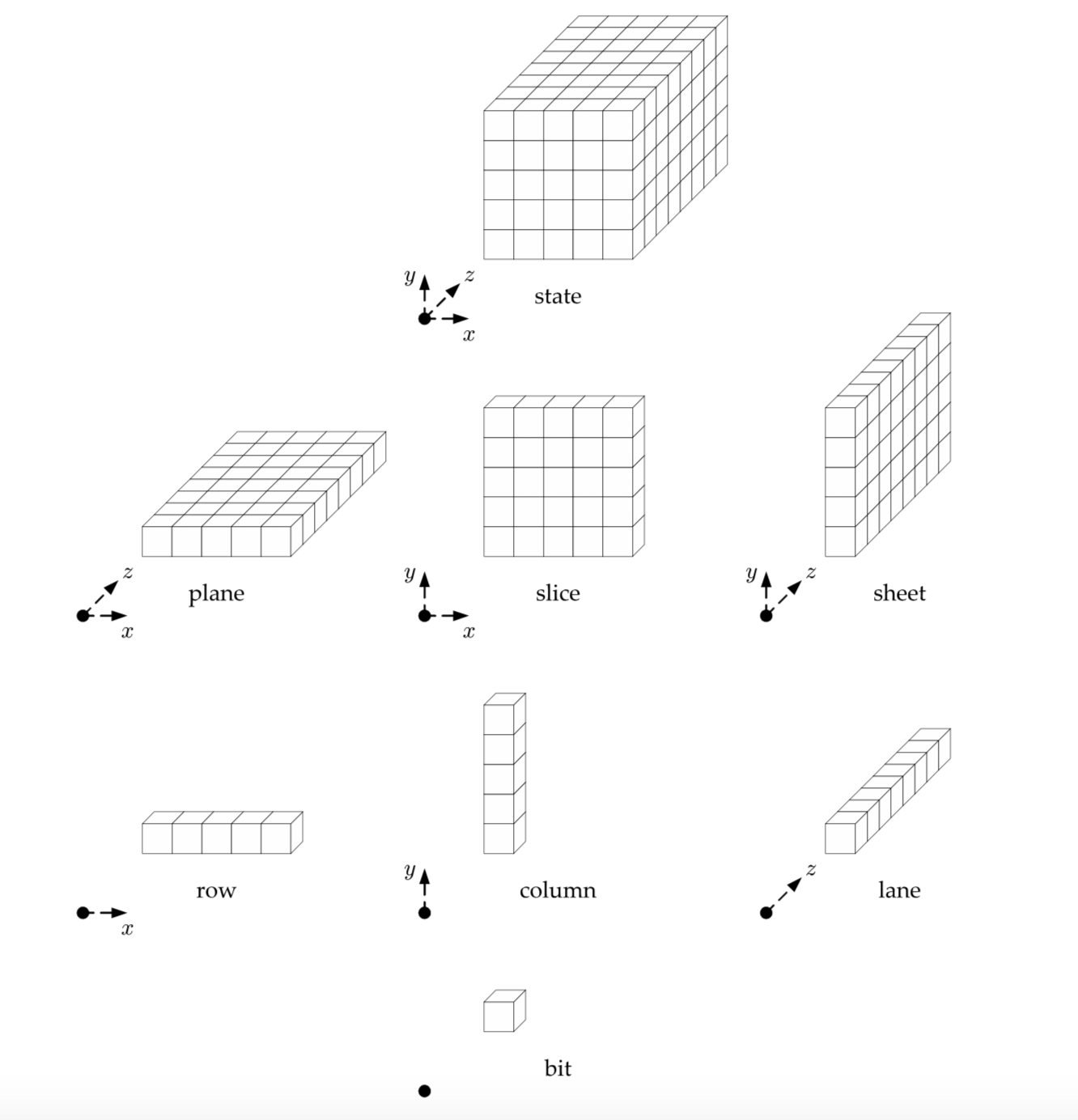
It is some sort of rectangular 3D object, and its different sub-objects have different names. Each little cube is a bit (a 1 or a 0). Cute.
I mean why not, AES was a square right? If we make it 3D we augment the security by one dimension. Sounds logical.
It gets weirder.
This is how the little cubes are indexed.
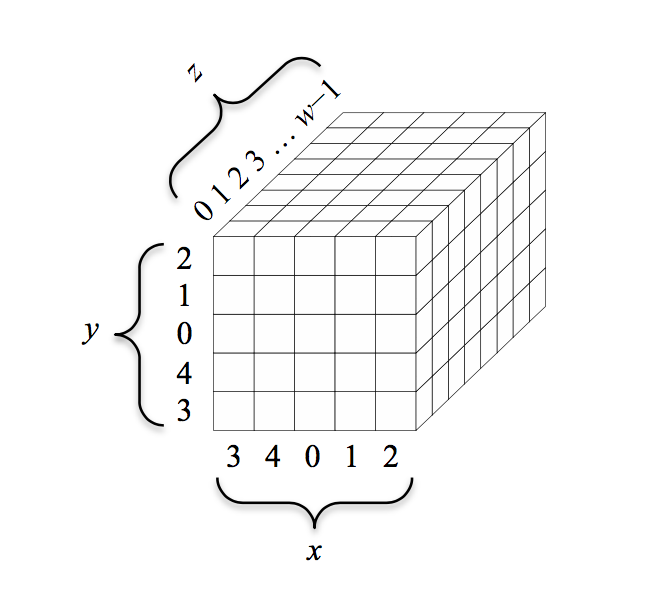
If you've started to reason on how you could translate that thing into a struct, stop. Don't overthink it. The x and y coordinates don't matter: all operations are done modulo the other columns or rows or you name it... you could have the indexes x = 0 and y = 0 anywhere really; it wouldn't change a thing. This picture doesn't even appear in Keccak's specification, only in FIPS 202. It is probably a joke from the NIST.
Multiple of bytes? Nopecheese
A uint8_t array
...you must have thought, still trying to have a head start, still shooting to figure out how you would stuck these bits in your code.
But wait. The NIST loves to think about bits though, not bytes. That's often surprising to people who end up implementing their specs with a byte length instead of a bit length and it led to what DJB calls a bit attack.
SHA-3 was no exception, NIST said to Keccak: you shall be able to handle the darkest desires of our stupid developers. You must account for ALL INPUTS. You must accept non-multiple of bytes.
Keccak provided. You can now hash 7-bit inputs with SHA-3.
The poor user is given enough rope with which to hang himself -- something a standard should not do.
—Rivest, 1992, commenting on the NIST/NSA “DSA” proposal
Bit indexing brainfudge
Let's talk about bit numbering, not byte order like big-endian and little-endian, no-no, bit numbering.
There are two ways to order bits in a byte (and we'll say here that a byte is an octet: it contains 8 bits):
- MSB first:
0x02 = 0000 0010, 0x01 = 0000 0001, ...
- LSB first:
0x40 = 0000 0010, 0x80 = 0000 0001, ...
Now what does this have to do with Keccak?
Keccak's bit numbering is LSB first, whereas NIST's one is MSB first (no kidding).
This means a re-mapping needs to take place when converting an input to the internal state of Keccak. This was all explained in the old specification of Keccak (see section 5).
Unfortunately these explanations disappeared in the latest version of the spec, and the NIST ended up writing up the conversion in an appendix (B.1) of their own specification FIPS 202.
Let me tell you: FIPS 202's explanation makes no sense. They end up mixing the theoretical internal state of Keccak with methods on how you can implement the re-mapping without having to inverse the bits of each bytes. It took me a while to figure it out and I am not the only one (most questions about Keccak/SHA-3 on internet end up being about their bit re-ordering).
Conclusion
Is SHA-3 Complicated? Some people would say no. But in reality there is no way to understand how to implement SHA-3 without looking at a reference implementation. NIST standards should seriously take a look at the process of TLS 1.3: no-one has been seen copying a reference implementation. Implementers are independently coding up what they understand of the draft specifications, and if cross-testing doesn't work it's either because they failed to understand something or because the specification needs some more love.
Having said that, Keccak is really cool and some of its applications look promising.
























