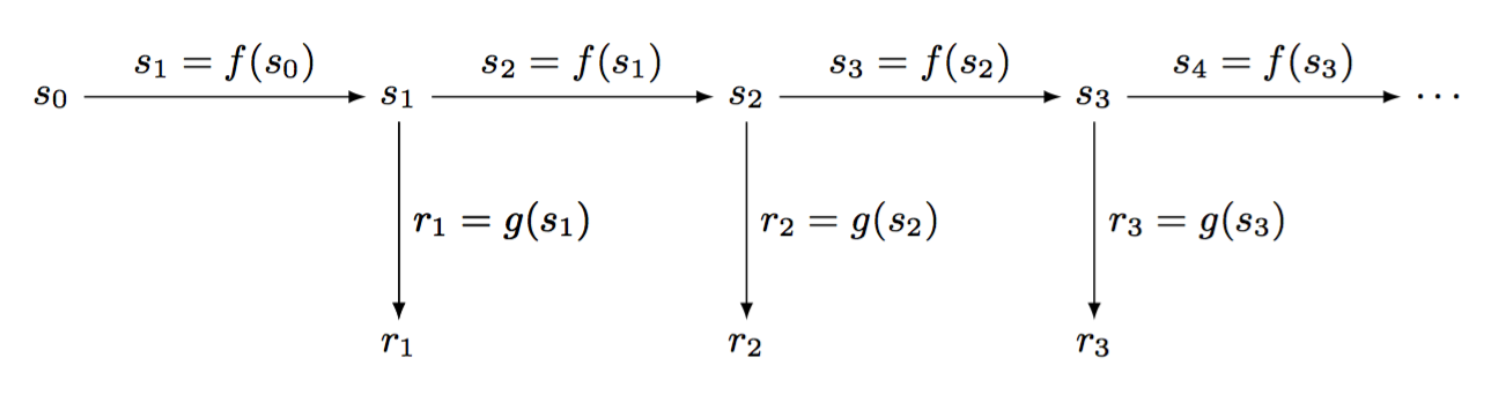Quick access to articles on this page:
more on the next page...
A few days ago, Juniper made an announcement on 2 backdoors in their ScreenOS application.
But no details were to be found in this advisory. Researchers from the twitter-sphere started digging, and finally the two flaws were found. The first vulnerability is rather crypto-y and this is what I will explain here.
First, some people realized by diffing strings of the patched and vulnerable binaries that some numbers were changed

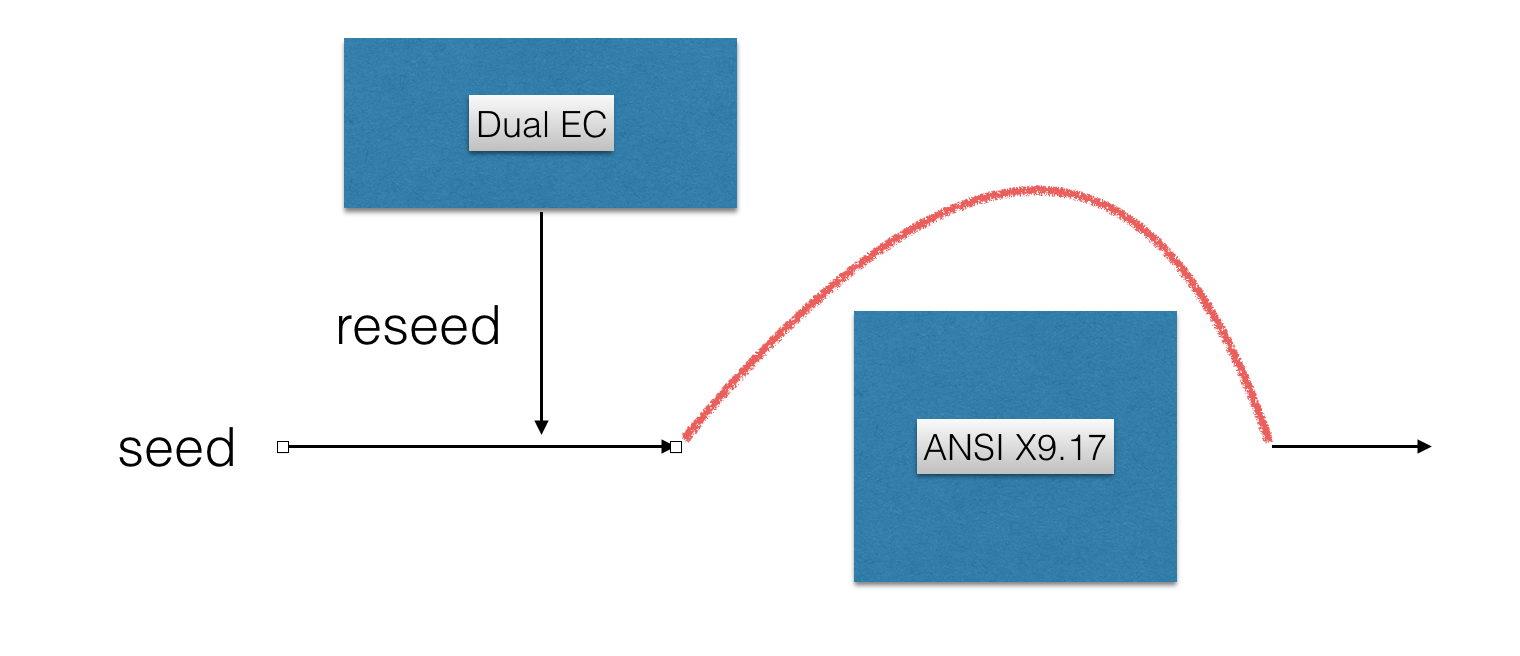
Then they realized that these numbers were next to the parameters of the P-256 NIST ECC curve. Worse, they realized that the modified values were these of the Dual EC PRNG: from a Juniper's product information page you could read that Dual EC had been removed from most of their products except ScreenOS. Why's that? No one knows, but they assured that the implementation was not visible from the outside, and thus the NSA's backdoor would be unusable.
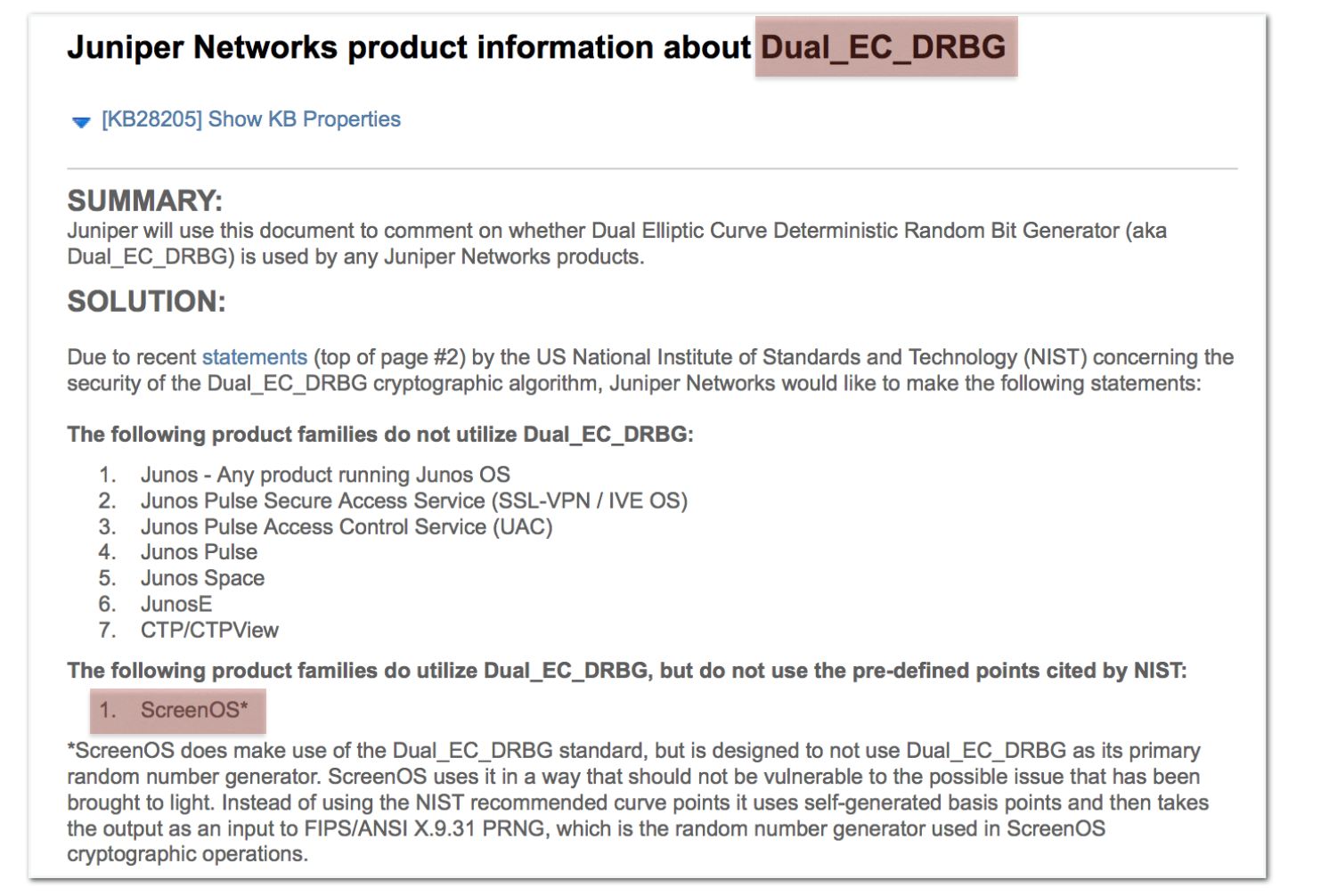
Actually, reading the values in their clean binaries, it looks like they had changed the NSA's values introducing their own \(Q\) point and thus canceling NSA's backdoor. But at the same time, maybe, introducing their own backdoor. Below the NSA's values for the point \(P\) and \(Q\) from the cached NIST publications:
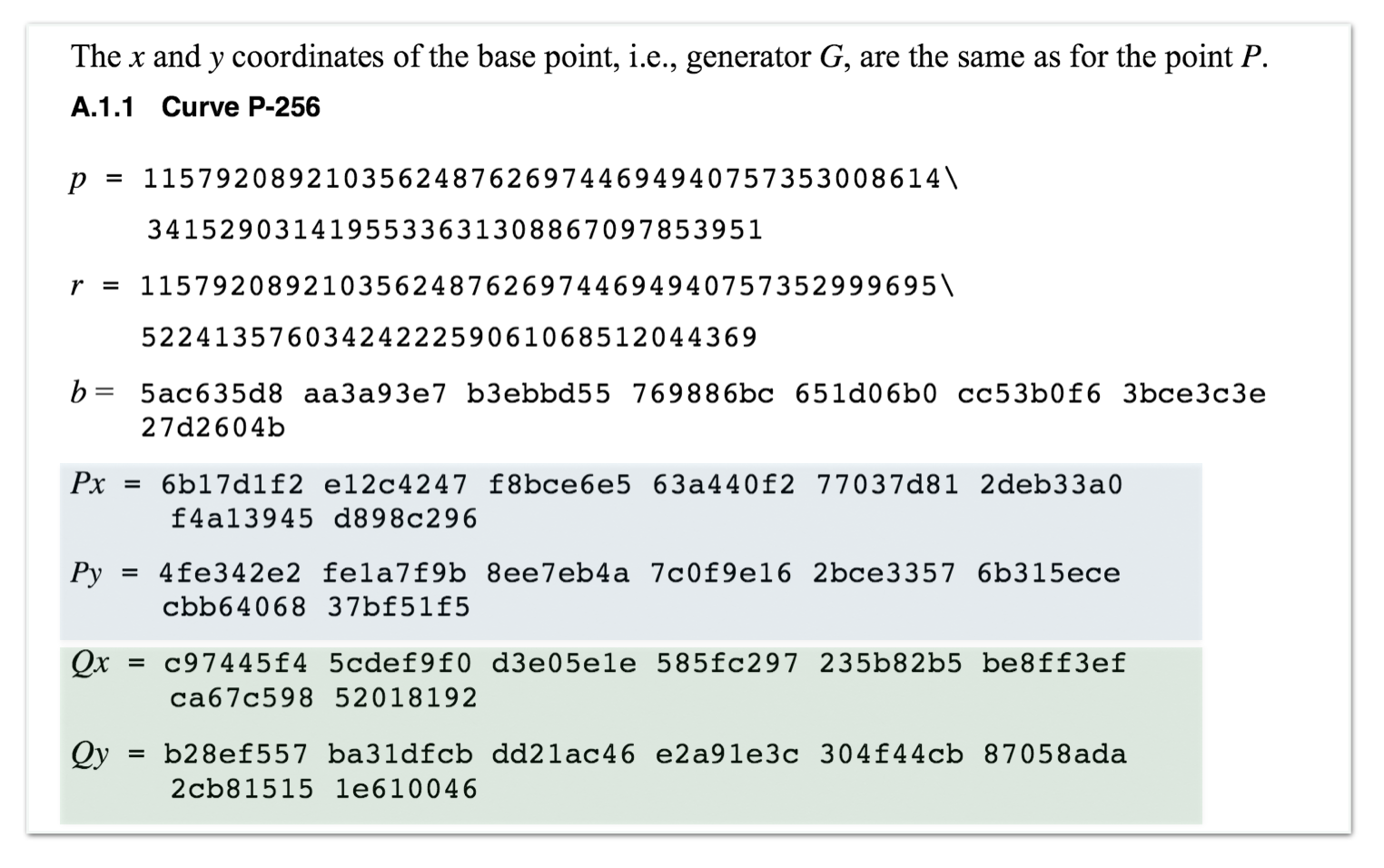
Reading the previous blog post, you can see how they could have easily modified \(Q\) to introduce their own backdoor. This doesn't mean that it is what they did. But at the time of the implementation, it was not really known that Dual EC was a backdoor, and thus there was no real reason to change these values.

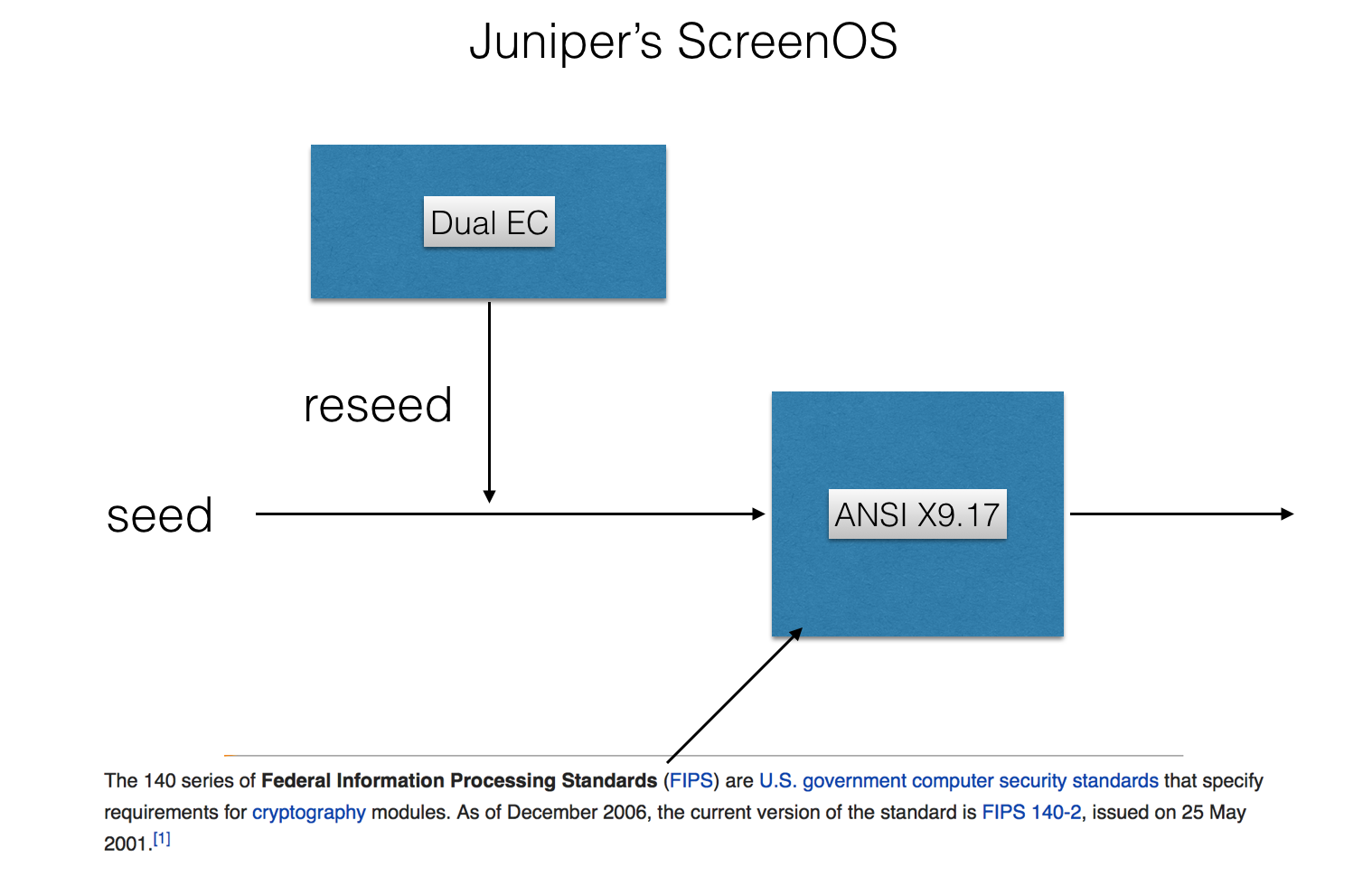
According to them, and the code, a second PRNG was used and Dual EC's only purpose was to help seeding it. Thus no real Dual EC output would see the surface of the program. The second PRNG was a FIPS approved one based on 3DES and is -- as far as I know -- deemed secure.
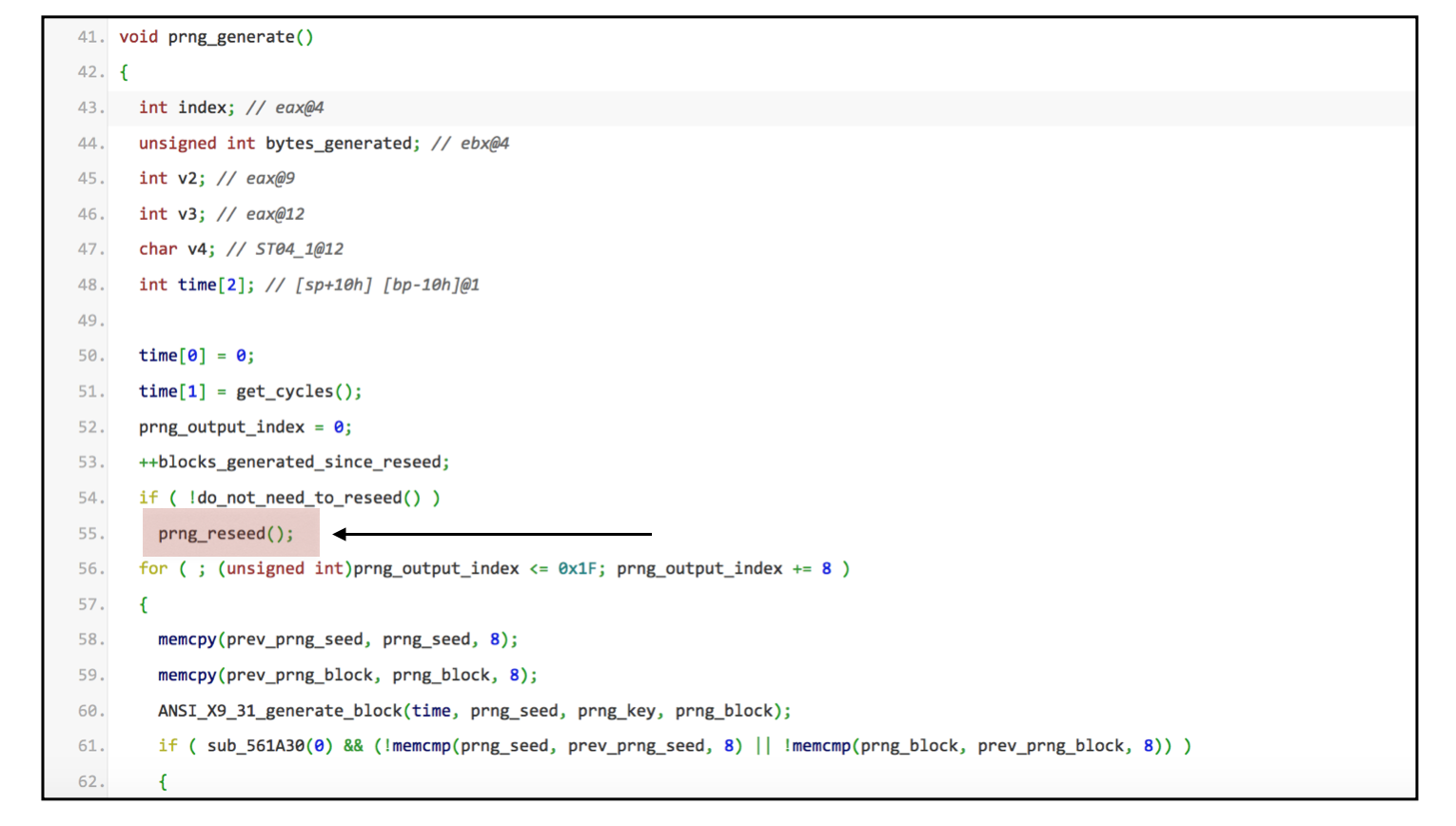
Another development came along and some others noticed that the call for the second PRNG was never made, this was because a global variable pnrg_output_index was always set to 32 through the prng_reseed() function.
Excerpt of the full code:
This advance was made because of Juniper's initial announcement that there were indeed two vulnerabilities. It seems like they were aware of the fact that Dual EC was the only PRNG being used in their code.
Now, how is the Dual EC backdoor controlled by the hackers? You could stop reading this post right now and just watch the video I made about Dual EC, but here are some more explanations anyway:
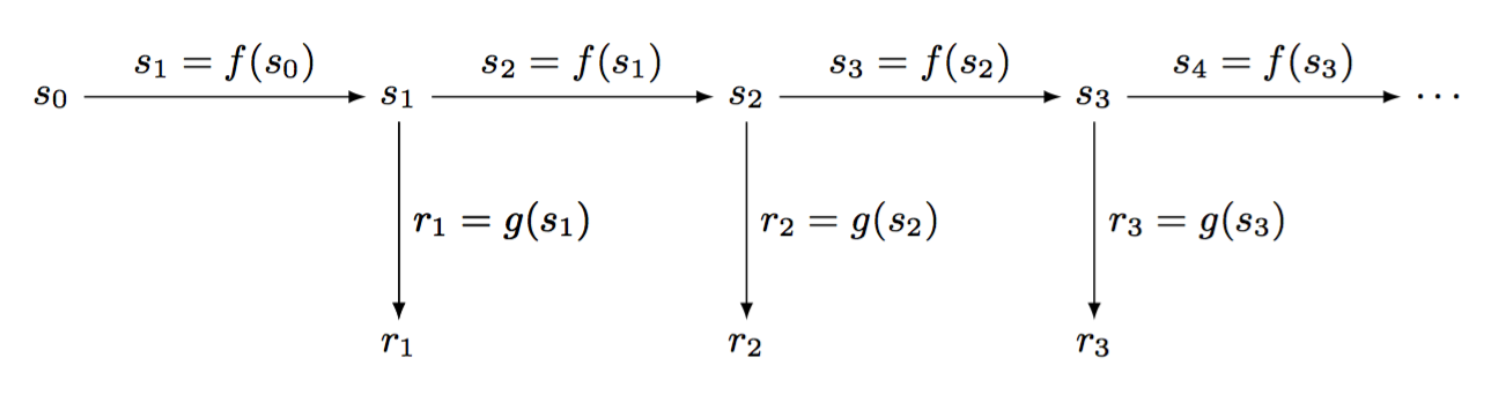
This above is the basis of a PRNG. You start it with a seed \(s_0\) and every time you need a random number you first create a new state from the current one (here with the function \(f\)), then you output a transformation of the state (here with the function \(g\)).
If the function \(g\) is one-way, the output doesn't allow you to retrieve the internal state and thus you can't predict future random numbers, neither retrieve past ones.
If the function \(f\) is one-way as well, retrieving the internal state doesn't allow you to retrieve past state and thus past random numbers generated by the PRNG. This makes the PRNG forward-secure.
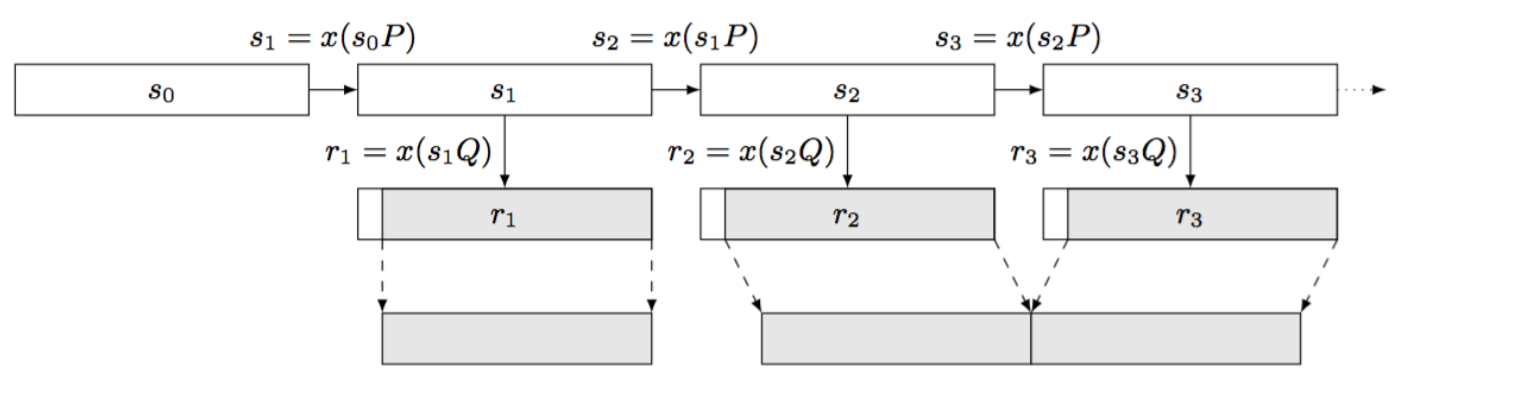
This is Dual EC. Iterating the state is done by multiplying the current state with the point \(P\) and then taking it's \(x\)-th coordinate. The point \(P\) is a point on a curve, with \(x\) and \(y\) coordinates, multiplying it with an integer gives us a new point on the curve. This is a one-way function because of the elliptic curve discrete logarithm problem and thus our PRNG is forward-secure (the ECDLP states that if you know \(P\) and \(Q\) in \(P = dQ\), it's really hard to find \(d\)).
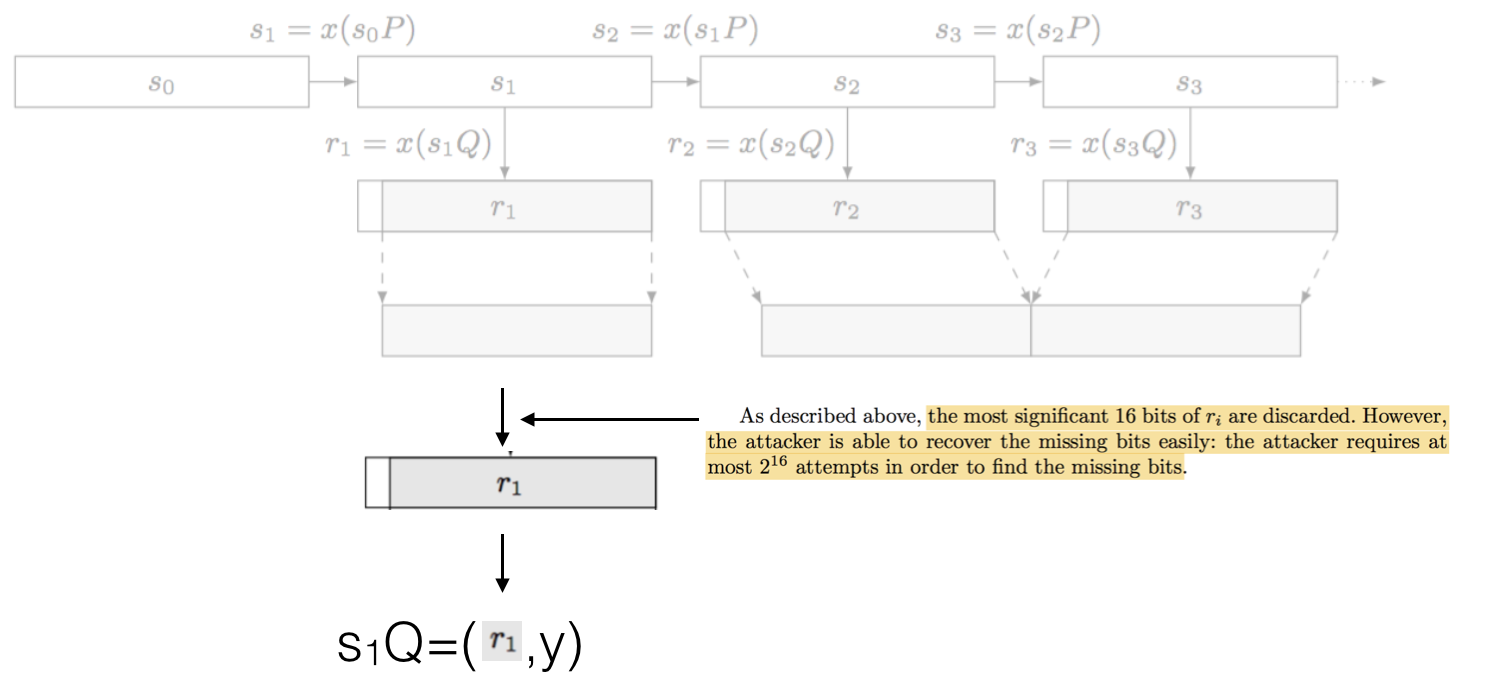
The interesting thing is that, in the attacker knows the secret integer \(d\) he can recover the next internal state of the PRNG. First, as seen above, the attacker recovers one random output, and then tries to get the full output: the real random output is done by truncating the first 16 bits of the full output. This is done in \(2^16\) iterations. Easy.
With our random number \(r_1\) (in our example), which is the \(x\) coordinate of our point \(s_1 Q\), we can easily recover the \(y\) coordinate and thus the entire point \(s_1 Q\). This is because of how elliptic curves are shaped.
Multiplying this point with our secret value \(d\) we obtain the next internal state as highlighted at the top of this picture:
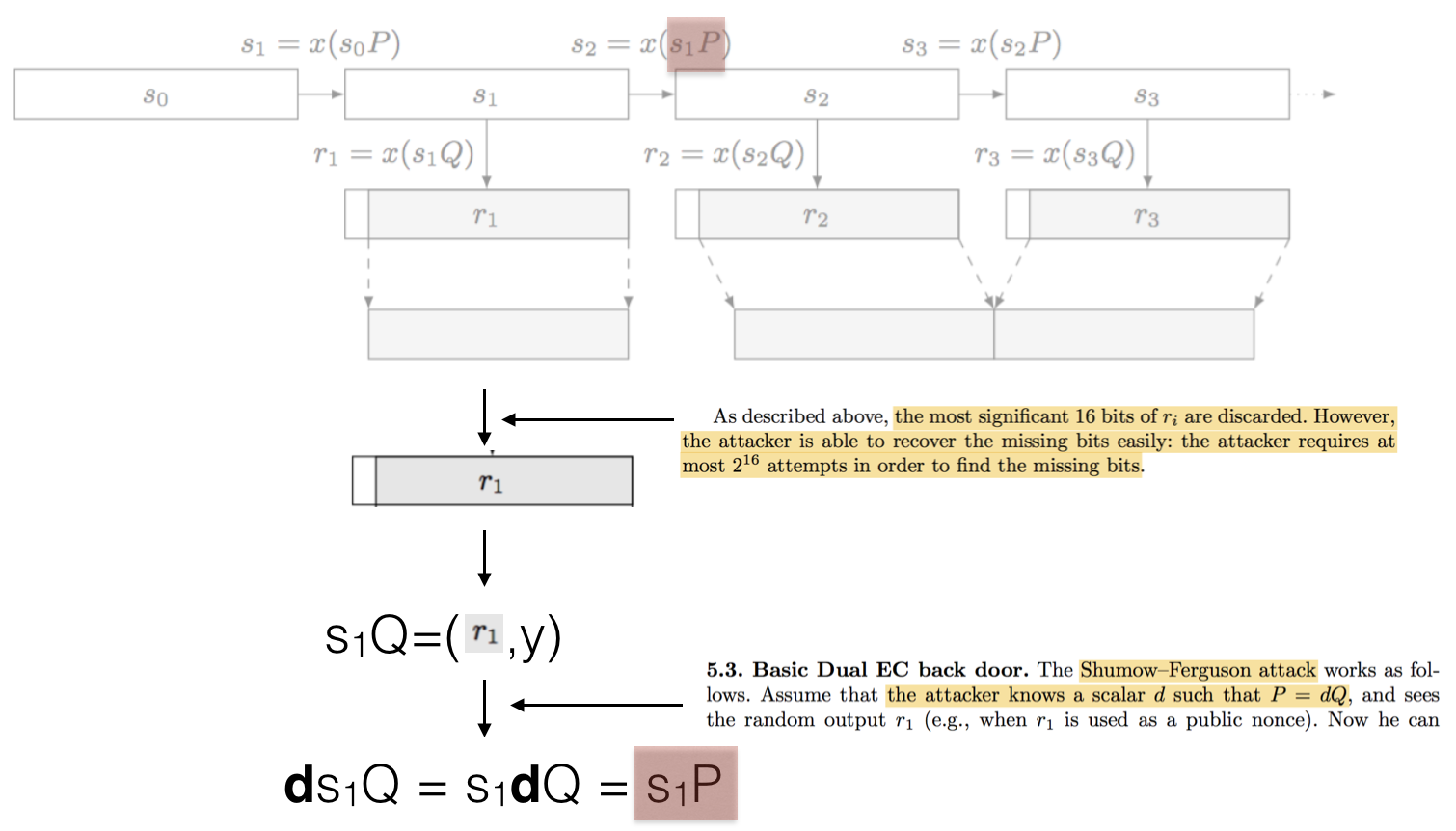
This attack is pretty destructive and in the order of mere minutes according to Dan Bernstein et al

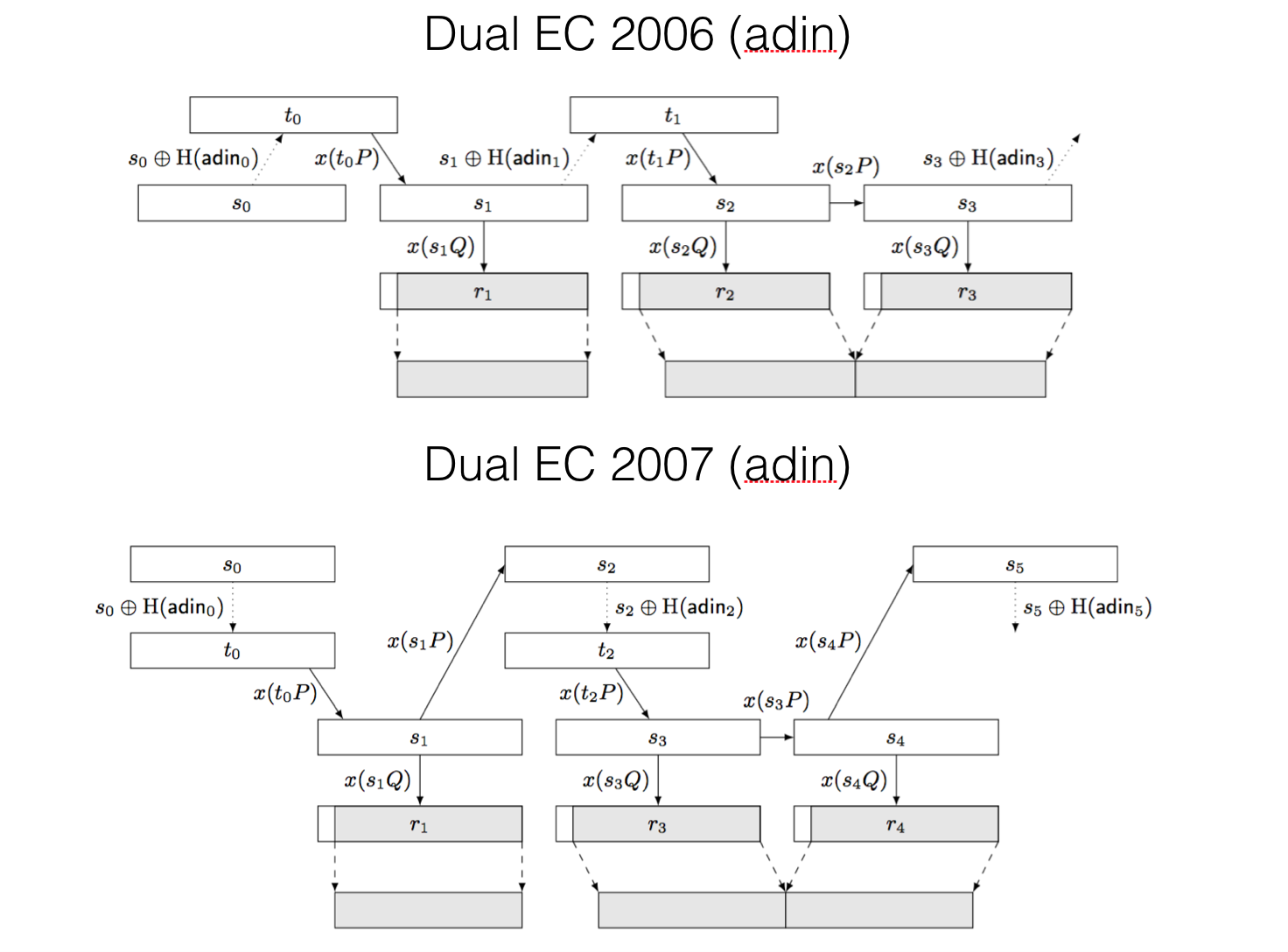
For completeness, it is important to know that there were two other constructions of the Dual EC PRNG with additional inputs, that allowed to add entropy to the internal state and thus provide backward secrecy: retrieving the internal state doesn't allow you to retrieve future states.
The first construction in 2006 broke the backdoor, the second in 2007 re-introduced it. Go figure...
tl;dr:
this is what you should type:
strings your_binary | grep -C5 -i "c97445f45cdef9f0d3e05e1e585fc297235b82b5be8ff3efca67c59852018192\|8e722de3125bddb05580164bfe20b8b432216a62926c57502ceede31c47816edd1e89769124179d0b695106428815065\|1b9fa3e518d683c6b65763694ac8efbaec6fab44f2276171a42726507dd08add4c3b3f4c1ebc5b1222ddba077f72943b24c3edfa0f85fe24d0c8c01591f0be6f63"
After all the Jupiner fiasco, I wondered how people could look if a binary contained an implementation of Dual EC, and worse, if it contained Dual EC with the NSA's values for P and Q.
The easier thing I could think of is the use of strings to check if the binary contains the hex values of some Dual EC parameters:
strings your_binary | grep -C5 -i `python -c "print '%x' % 115792089210356248762697446949407573530086143415290314195533631308867097853951"`
This is the value of the prime p of the curve P-256. Other curves can be used for Dual EC though, so you should also check for the curve P-384:
strings your_binary | grep -C5 -i `python -c "print '%x' % 39402006196394479212279040100143613805079739270465446667948293404245721771496870329047266088258938001861606973112319"`
and the curve P-521:
strings your_binary | grep -C5 -i `python -c "print '%x' % 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151 "`
I checked the binaries of ScreenOS (taken from here) and they contained these three curves parameters. But this doesn't mean anything, just that these curves are stored, maybe used, maybe used for Dual EC...
To check if it uses the NSA's P and Q, you should grep for P and Q x coordinates from the same NIST paper.

This looks for all the x coordinates of the different P for each curves. This is not that informative since it is the standard point P as a generator of P-256
strings your_binary | grep -C5 -i "6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296\|aa87ca22be8b05378eb1c71ef320ad746e1d3b628ba79b9859f741e082542a385502f25dbf55296c3a545e3872760ab7\|c6858e06b70404e9cd9e3ecb662395b4429c648139053fb521f828af606b4d3dbaa14b5e77efe75928fe1dc127a2ffa8de3348b3c1856a429bf97e7e31c2e5bd66"
Testing the ScreenOS binaries, I get all the matches. This means that the parameters for P-256 and maybe Dual EC are indeed stored in the binaries.
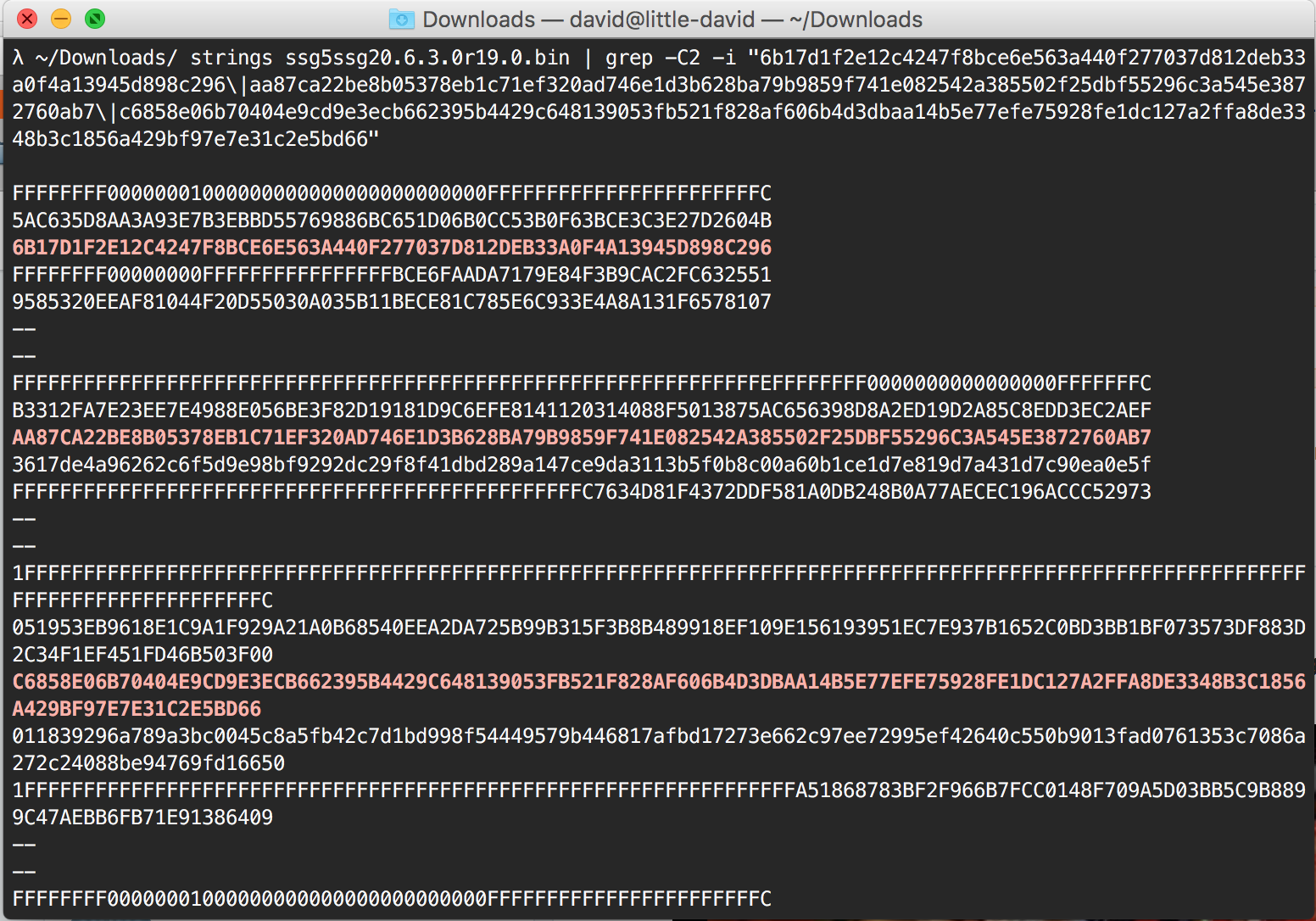
weirdly, testing for Qs I don't get any match. So Dual EC or not?
strings your_binary | grep -C5 -i "c97445f45cdef9f0d3e05e1e585fc297235b82b5be8ff3efca67c59852018192\|8e722de3125bddb05580164bfe20b8b432216a62926c57502ceede31c47816edd1e89769124179d0b695106428815065\|1b9fa3e518d683c6b65763694ac8efbaec6fab44f2276171a42726507dd08add4c3b3f4c1ebc5b1222ddba077f72943b24c3edfa0f85fe24d0c8c01591f0be6f63"
Re-reading CVE-2015-7765:
The Dual_EC_DRBG 'Q' parameter was replaced with 9585320EEAF81044F20D55030A035B11BECE81C785E6C933E4A8A131F6578107 and the secondary ANSI X.9.31 PRNG was broken, allowing raw Dual_EC output to be exposed to the network. Please see this blog post for more information.
Diffing the vulnerable (and patched binaries. I see that only the P-256 curve \(Q\) was modified from Juniper's values, other curves were left intact. I guess this means that only the P-256 curve was being used in Dual EC.
If you know how Dual EC works (if you don't check my video), you know that to establish a backdoor into it you need to generate \(P\) and \(Q\) accordingly. So changing the value \(Q\) with no correlation to \(P\) is not going to work, worse it could be that \(Q\) is too "close" to P and thus the secret \(d\) linking them could be easily found ( \(P = dQ \)).
Now one clever way to generate a secure \(Q\) with a strong value \(d\) that only you would know is to choose a large and random \(d\) and calculate its inverse \(d^{-1} \pmod{ord_{E}} \). You have your \(Q\) and your \(d\)!
\[ d^{-1} P = Q \]
bonus: here's a small script that attempts to find \(d\) in the hypothesis \(d\) would be small (the fastest way to compute an elliptic curve discrete log is to use Pollard Rho's algorithm)
p256 = 115792089210356248762697446949407573530086143415290314195533631308867097853951
a256 = p256 - 3
b256 = 41058363725152142129326129780047268409114441015993725554835256314039467401291
## base point values
gx = 48439561293906451759052585252797914202762949526041747995844080717082404635286
gy = 36134250956749795798585127919587881956611106672985015071877198253568414405109
## order of the curve
qq = 115792089210356248762697446949407573529996955224135760342422259061068512044369
# init curve
FF = GF(p256)
EE = EllipticCurve([FF(a256), FF(b256)])
# define the base point
G = EE(FF(gx), FF(gy))
# P and Q
P = EE(FF(0x6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296), FF(0x4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5))
# What is Q_y ?
fakeQ_x = FF(0x9585320EEAF81044F20D55030A035B11BECE81C785E6C933E4A8A131F6578107)
fakeQ = EE.lift_x(fakeQ_x)
print discrete_log(P, fakeQ, fakeQ.order(), operation='+')
The lift_x function allows me to get back the \(y\) coordinate of the new \(Q\):
EE.lift_x(fakeQ_x)
(67629950588023933528541229604710117449302072530149437760903126201748084457735 : 36302909024827150197051335911751453929694646558289630356143881318153389358554 : 1)
Short blogpost on a quick way to analyze a TLS handshake:
In one terminal, setup the server:
openssl req -x509 -newkey rsa:2048 -keyout key.pem -out cert.pem -nodes
openssl s_server -cert cert.pem -key key.pem
The first command use the req toolkit of openssl. It is usually used to create certificate request (and the request is then later approved by a CA), but since we're in a rush, let's just use it with the -x509 option to directly generate a certificate. rsa:2048 generates a key with the algorithm RSA and with a modulus of size 2048 bits. -nodes disable the use of a passphrase to protect the key (the default protect the key by encrypting it with DES).
In a second terminal, start capturing packets:
tcpdump -i lo0 -s 65535 -w exchange.cap
65535 is the maximum length of a packet.
Start a handshake in a third terminal:
openssl s_client -connect localhost:4433
Now open the .cap with Wireshark!
Heard a bit late about the factorable research results and how they used batch gcd to recover a bunch of servers' private keys.
The question one could think of is how to efficiently do a batch gcd on a big set of public keys?
From this utility:
- Actual pairwise GCD
This performs n*(n-1)/2 GCD operations on the moduli. This is slow. Don't use this.
- Accumulating Product
This iterates over all input moduli, performing a GCD of each one against the product of all previous.
Once it finds a candidate, it scans all previous moduli to find out which ones it shared a factor with
(either GCD or division, depending on whether one or both were found).
The main scan cannot be done in parallel, and even though it seems like this is O(n), the increasing size
of the accumulated product results it lots of long multiplication and long divison so it's still painfully
slow for large numbers of moduli.
Looks like the most efficient ways come from Dan Bernstein (again!), in a 7 pages paper
the Threat Model for BGP Path Security document lists, as RFCs usually do, relevant terms with their respective definitions. It can be a quick way to get an understanding of these abbreviations you often come across but never dare to google:
-
Autonomous System (AS): An AS is a set of one or more IP networks operated by a single administrative entity.
-
AS Number (ASN): An ASN is a 2- or 4-byte number issued by a registry to identify an AS in BGP.
-
Border Gateway Protocol (BGP): A path vector protocol used to convey "reachability" information among ASes in support of inter-domain routing.
-
False (Route) Origination: If a network operator originates a route for a prefix that the operator does not hold (and that has not been authorized to originate by the prefix holder), this is termed false route origination.
-
Internet Service Provider (ISP): An organization managing (and typically selling) Internet services to other organizations or individuals.
-
Internet Number Resources (INRs): IPv4 or IPv6 address space and ASNs.
-
Internet Registry: An organization that manages the allocation or distribution of INRs. This encompasses the Internet Assigned Number Authority (IANA), Regional Internet Registries (RIRs), National Internet Registries (NIRs), and Local Internet Registries (LIRs) (network operators).
-
Network Operator: An entity that manages an AS and thus emits (E)BGP updates, e.g., an ISP.
-
Network Operations Center (NOC): A network operator employs a set of equipment and a staff to manage a network, typically on a 24/7 basis. The equipment and staff are often referred to as the NOC for the network.
-
Prefix: A prefix is an IP address and a mask used to specify a set of addresses that are grouped together for purposes of routing.
-
Public Key Infrastructure (PKI): A PKI is a collection of hardware, software, people, policies, and procedures used to create, manage, distribute, store, and revoke digital certificates.
-
Relying Parties (RPs): An RP is an entity that makes use of signed products from a PKI, i.e., it relies on signed data that is verified using certificates and Certificate Revocation Lists (CRLs) from a PKI.
-
RPKI Repository System: The RPKI repository system consists of a distributed set of loosely synchronized databases.
-
Resource PKI (RPKI): A PKI operated by the entities that manage INRs and that issue X.509 certificates (and CRLs) that attest to the holdings of INRs.
-
RPKI Signed Object: An RPKI signed object is a data object encapsulated with Cryptographic Message Syntax (CMS) that complies with the format and semantics defined in [RFC6488].
-
Route: In the Internet, a route is a prefix and an associated sequence of ASNs that indicates a path via which traffic destined for the prefix can be directed. (The route includes the origin AS.)
- Route Leak: A route leak is said to occur when AS-A advertises routes that it has received from AS-B to the neighbors of AS-A, but AS-A is not viewed as a transit provider for the prefixes in the route.
In cryptography, zeroisation (also spelled zeroization) is the practice of erasing sensitive parameters (electronically stored data, cryptographic keys, and CSPs) from a cryptographic module to prevent their disclosure if the equipment is captured. This is generally accomplished by altering or deleting the contents to prevent recovery of the data. When encryption was performed by mechanical devices, this would often mean changing all the machine's settings to some fixed, meaningless value, such as zero. On machines with letter settings rather than numerals, the letter 'O' was often used instead. Some machines had a button or lever for performing this process in a single step. Zeroisation would typically be performed at the end of an encryption session to prevent accidental disclosure of the keys, or immediately when there was a risk of capture by an adversary.
from Wikipedia
The Mcgrew draft (on the old stateful signature scheme LMS) has a section on "how not to mess with implementing a stateful scheme". It's pretty scary.
The LMS signature system, like all N-time signature systems, requires
that the signer maintain state across different invocations of the
signing algorithm, to ensure that none of the component one-time
signature systems are used more than once. This section calls out
some important practical considerations around this statefulness.
In a typical computing environment, a private key will be stored in
non-volatile media such as on a hard drive. Before it is used to
sign a message, it will be read into an application's Random Access
Memory (RAM). After a signature is generated, the value of the
private key will need to be updated by writing the new value of the
private key into non-volatile storage. It is essential for security
that the application ensure that this value is actually written into
that storage, yet there may be one or more memory caches between it
and the application. Memory caching is commonly done in the file
system, and in a physical memory unit on the hard disk that is dedicated to that purpose. To ensure that the updated value is
written to physical media, the application may need to take several
special steps. In a POSIX environment, for instance,the O_SYNC flag
(for the open() system call) will cause invocations of the write()
system call to block the calling process until the data has been to
the underlying hardware. However, if that hardware has its own
memory cache, it must be separately dealt with using an operating
system or device specific tool such as hdparm to flush the on-drive
cache, or turn off write caching for that drive. Because these
details vary across different operating systems and devices, this
note does not attempt to provide complete guidance; instead, we call
the implementer's attention to these issues.
When hierarchical signatures are used, an easy way to minimize the
private key synchronization issues is to have the private key for the
second level resident in RAM only, and never write that value into
non-volatile memory. A new second level public/private key pair will
be generated whenever the application (re)starts; thus, failures such
as a power outage or application crash are automatically
accommodated. Implementations SHOULD use this approach wherever
possible.
This post is the ending of a series of blogposts on hash-based signatures. You can find part I here
So now we're getting into the interesting part, the real signatures schemes.
PQCrypto has released an initial recommendations document a few months ago. The two post-quantum algorithms advised there were XMSS and SPHINCS:

This blogpost will be presenting XMSS, a stateful signature scheme, while the next will focus on SPHINCS, the first stateless signature scheme!
XMSS
The eXtended Merkle Signature Scheme (XMSS) was introduced in 2011 and became an internet-draft in 2015.
The main construction looks like a Merkle tree, excepts a few things. The XMSS tree has a mask XORed to the child nodes before getting hashed in their parents node. It's a different mask for every node:
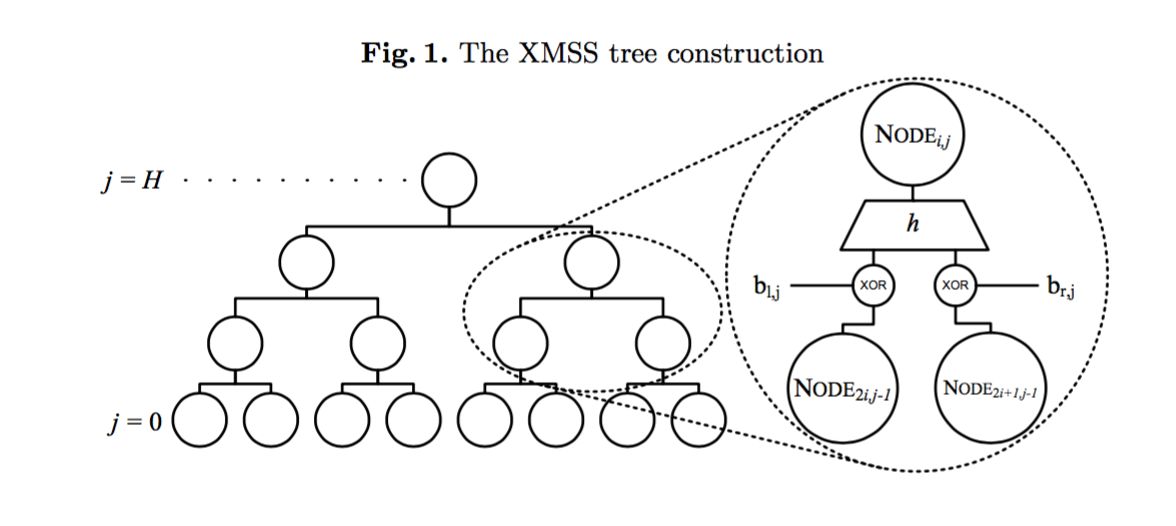
The second particularity is that a leaf of the XMSS tree is not a hash of a one-time signature public key, but the root of another tree called a L-tree.
A L-tree has the same idea of masks applied to its nodes hashes, different from the main XMSS Trees, but common to all the L-trees.
Inside the leaves of any L-tree are stored the elements of a WOTS+ public key. This scheme is explained at the end of the first article of this series.
If like me you're wondering why they store a WOTS+ public key in a tree, here's what Huelsing has to say about it:
The tree is not used to store a WOTS public key but to hash it in a way that we can prove that a second-preimage resistant hash function suffices (instead of a collision resistant one).
Also, the main public key is composed of the root node of the XMSS tree as well as the bit masks used in the XMSS tree and a L-tree.
SPHINCS
SPHINCS is the more recent one, combining a good numbers of advances in the field and even more! Bringing the statelessness we were all waiting for.
Yup, this means that you don't have to keep the state anymore. But before explaining how they did that, let's see how SPHINCS works.
First, SPHINCS is made out of many trees.
Let's look at the first tree:
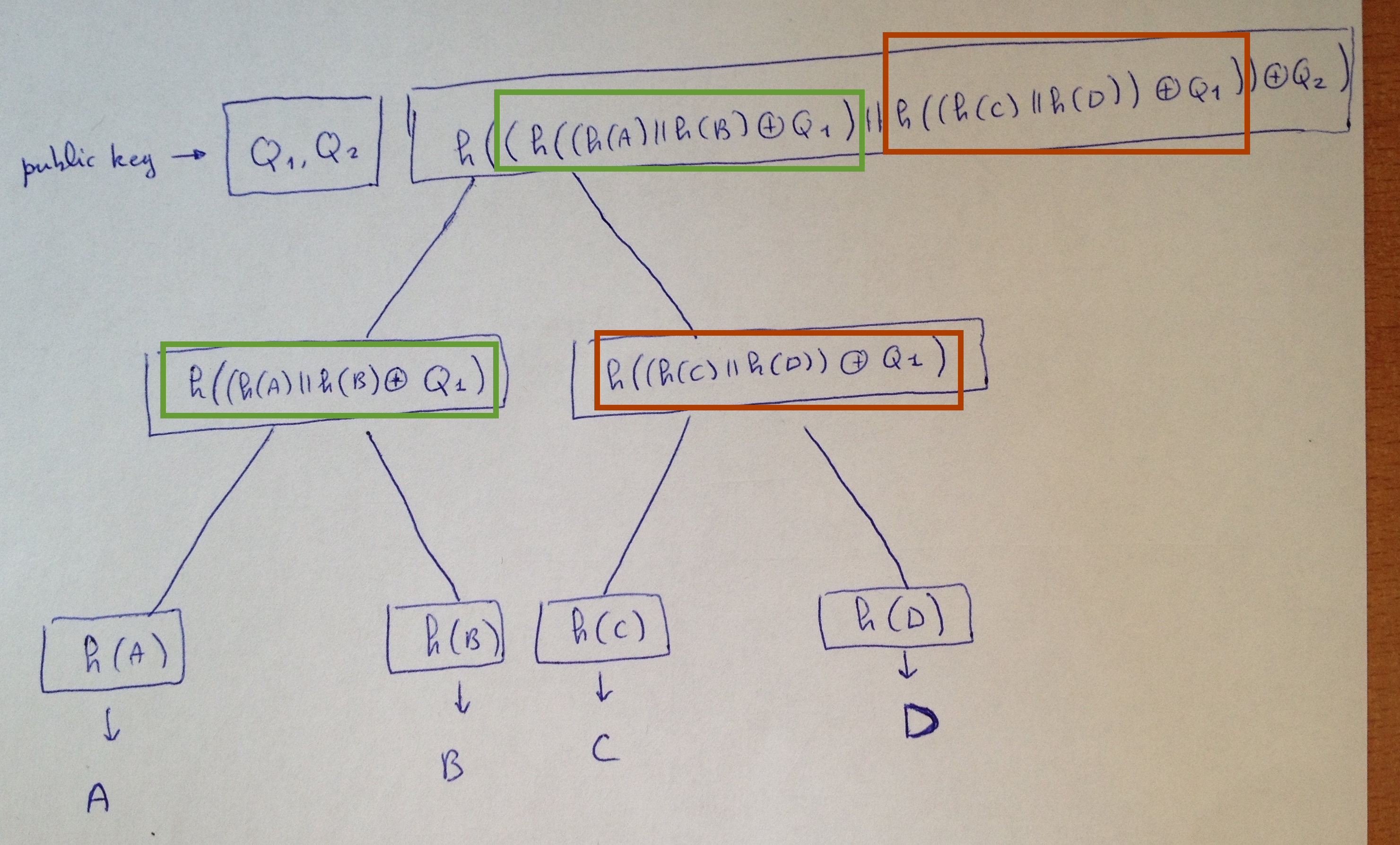
- Each node is the hash of the XOR of the concatenation of the previous nodes with a level bitmask.
- The public key is the root hash along with the bitmasks.
- The leaves of the tree are the compressed public keys of WOTS+ L-trees.
See the WOTS+ L-trees as the same XMSS L-tree we previously explained, except that the bitmask part looks more like a SPHINCS hash tree (a unique mask per level).
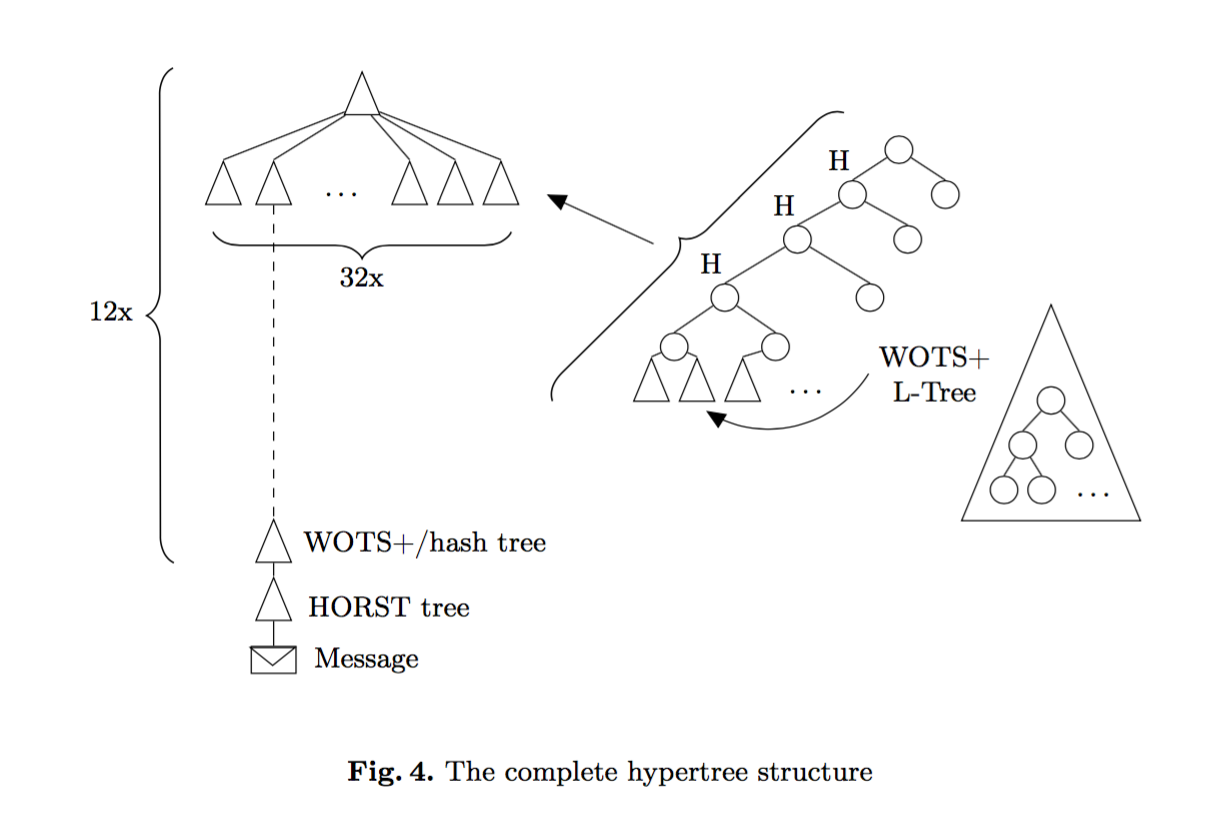
Each leaves, containing one Winternitz one-time signature, allow us to sign another tree. So that we know have a second layer of 4 SPHINCS trees, containing themselves WOTS+ public keys at their leaves.
This go on and on... according to your initial parameter. Finally when you reach the layer 0, the WOTS+ signatures won't sign other SPHINCS trees but HORS trees.
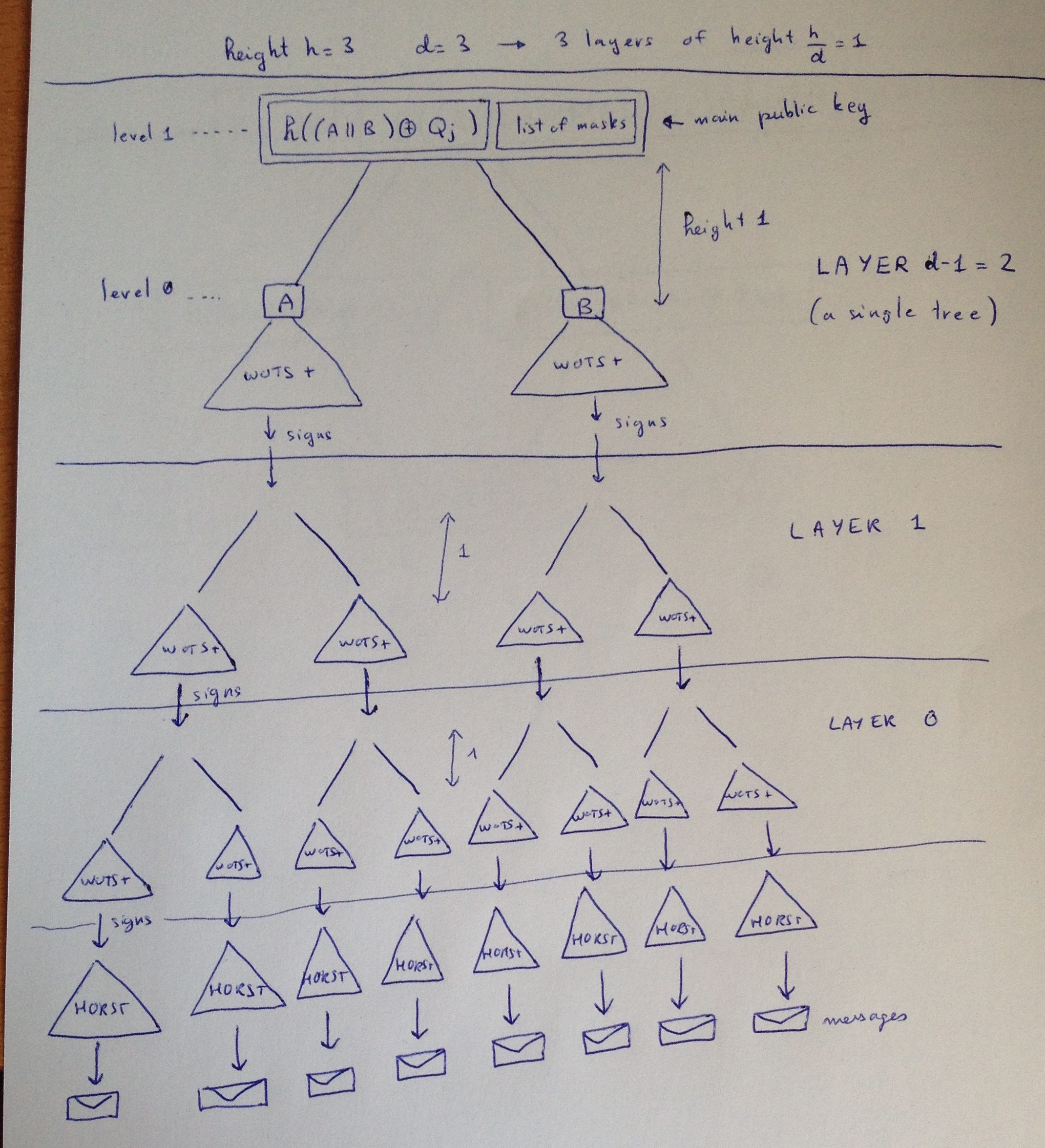
A HORST or HORS tree is the same as a L-tree but this time containing a HORS few-time signature instead of a Winternitz one-time signature. We will use them to sign our messages, and this will increase the security of the scheme since if we do sign a message with the same HORS key it won't be a disaster.
Here's a diagram taken out of the SPHINCS paper making abstraction of WOTS+ L-trees (displaying them as signature of the next SPHINCS tree) and showing only one path to a message.

When signing a message M you first create a "randomized" hash of M and a "random" index. I put random in quotes because everything in SPHINCS is deterministically computed with a PRF. The index now tells you what HORST to pick to sign the randomized hash of M. This is how you get rid of the state: by picking an index deterministically according to the message. Signing the same message again should use the same HORST, signing two different messages should make use of two different HORST with good probabilities.
And this is how this series end!
EDIT: here's another diagram from Armed SPHINCS, I find it pretty nice!